Реализации гиперграфа

Пусть задан гиперграф Н=(V, E). Реализацией гиперграфа Н называется любой граф G, удовлетворяющий следующим условиям:

1) VG = VH;

2) любое ребро графа G содержится в некотором ребре гиперграфа Н;

3) для любого ребра е € E порожденный подграф G(e)является связным.

Реализацией ребра е € E гиперграфа Н является любой связный граф G_e, для которого VG_e = e. Поэтому

всякая реализация гиперграфа является объединением некоторых реализаций всех его ребер.

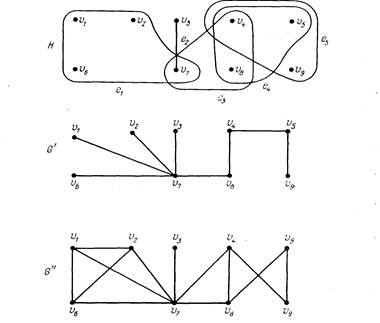
На рис. 71.1 изображены гиперграф Н и две его реализации G’ и С",

Задачи построения реализации гиперграфов часто возникают в электронике при проектировании и изготовлении интегральных схем. Элементы такой схемы, как правило, разбиты на группы. При изготовлении схемы элементы каждой группы должны быть соединены проводниками. Таким образом, можно считать, что спроектированная схема задается с помощью гиперграфа, а изготовленная — с помощью графа, являющегося реализацией заданного гиперграфа. При этом соединять элементы можно произвольным способом, лишь бы получающийся в результате граф обладал заданными свойствами, например, был деревом, планарным или гамильтоновым графом и т. д. Следует отметить, что, как правило, задачи построения подобных реализаций являются очень сложными для алгоритмического решения.

Сначала рассмотрим реализацию гиперграфа деревом. Для этого введем определения.

Реберным графом гиперграфа Н =(V, E) называется граф L(Н) = (E,E), множество вершин которого совпадает с множеством ребер E гиперграфа Н, при этом две вершины графа L(H) смежны тогда и только тогда, когда смежны соответствующие им ребра гиперграфа Н. Таким образом, L(Н)— граф пересечений ребер гиперграфа Н.

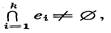Говорят, что множество {e₁, e₂, ..., e_r} попарно смежных ребер удовлетворяет условию Хелли, если

или,другими словами, если существует по крайней мере одна общая вершина, инцидентная каждому ребру e_i

Если любое множество попарно смежных ребер гиперграфа Н удовлетворяет условию Хелли, то говорят, что гиперграф Н удовлетворяет условию Хелли.

Теорема 71.1.Реализация связного гиперграфа Н деревом существует тогда и только тогда, когда Н удовлетворяет условию Хелли, а реберный граф L(H) триангулированный.

Необходимость. Пусть для гиперграфа Н существует его реализация деревом Т. Сначала покажем, что Н удовлетворяет условию Хелли. Доказательство проведем индукцией по мощности множества попарно смежных ребер гиперграфа Н.

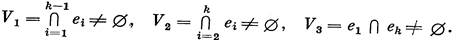Два смежных ребра, конечно, удовлетворяют условию Хелли. Преположим, что любое множество попарно смежных ребер в количестве к — 1 > 2 удовлетворяет условию Хелли, и рассмотрим множество {e₁, e₂, ..., e_r} попарно смежных ребер гиперграфа Н. По индуктивному предположению

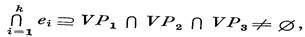Очевидно, что если хотя бы одно из пересечений V_i ∩ V_j ( i ≠ j, i,j = 1, 3) непусто, то непусто и ∩ e_i , а значит, любые k попарно смежных ребер удовлетворяют условию Хелли. Поэтому остается рассмотреть случай,, когда существуют три различные вершины и ≡ V₁, v € V₂и w € V₃. Введем следующие обозначения: P₁ —(и, v)-цепь, P₂—{v, w}-цепь, P₃—( и, w)-цепь в графе Т. Так как; Т — дерево, то VP₁ ∩ VP₂ ∩ VP₃ ≠ ¢ (иначе граф T содержал бы цикл). В то же время всякое ребро e_i (i =1, k) содержит не менее двух вершин из {и, v, w}, и реализацией e_i является дерево T_i. Поэтому всякое дерево T_i (i = 1, k) содержит все вершины одной из цепей P₁, P₂, P₃ Отсюда имеем

т. е. множество {e₁, e₂, ..., e_r} удовлетворяет условию Хелли. Следовательно, гиперграф удовлетворяет условию Хелли.

Теперь методом от противного покажем, что реберный граф L(H) = (E, E) является триангулированным. Пусть в L.(H) существует порожденный простой цикл С={e₁, e₂, ..., e_p, e₁}, р ≥ 4. Тогда этому циклу в Н соответствуют ребра e₁, e₂, ..., e_p, такие, что смежными среди них являются лишь пары ребер е₁ и е₂, е₂ и е₃, …., е_p и е₁ (рис. 71.2), а это значит, что при реализации ребер e₁, e₂, ..., e_p появится цикл. Однако это противоречит тому, что реализация Т гиперграфа Н является деревом.

Достаточность. Рассмотрим класс H связных гиперграфов H , каждый из которых удовлетворяет условию Хелли, реберный граф L (Н) является триангулированным. Докажем, что существует реализация любого гиперграфа l € H деревом.

Доказательство проведем индукцией по числу ребер типерграфа. Для гиперграфов с одним ребром утверждение очевидно. Пусть гиперграф H = (V, E) € H имеет т ≥ 2 ребер (|E|=т) и реализация деревом любого гиперграфа из H с меньшим числом ребер существует. Поскольку граф L (Н) = (E, Е) триангулированный, то в нем потеореме 62.4 существует симплициальная вершина e₀, т. е. множество вершин e₀ U N(e₀) является кликой в L(H). Этой вершине в гиперграфе Н соответствует ребро e₀, все смежные ребра которого обозначим через e₁, e₂, ..., e_k .Так как они соответствуют вершинам N(e₀) графа L(H), то для любых i = 1, k, j = 1, k справедливо соотношение e_i ∩ e_j ≠ ¢.

Поскольку гиперграф H удовлетворяет условию Хелли, то существует вершина v₀ € ∩ e_i . Теперь рассмотрим

новый гиперграф Н' = (V’, E’), где V’ = V \( e₀ \ v₀), E' = {е' : е' ≡ e \ (e_o \ v_o), e € E, е ≠ e₀). Итак, |E'| = |E| - 1 = т - 1. Поскольку ребра е'₁, е'₂, ..., е'_k содержат вершину v_o , а остальные ребра гиперграфа Н' остались прежними (е’ = е), то гиперграф Н' также удовлетворяет условию Хелли. По той же причине граф L(H') изоморфен графу, полученному из L(H) путем удаления вершины, соответствующей ребру во, т. е. L(H’) — триангулированный граф. Следовательно, Н' € H.

Поскольку |E'| = т — 1, то по индуктивному предположедию существует реализация гиперграфа Н' = (V’,E') деревом Т'. Очевидно, что реализация гиперграфа Н деревом Т получается из дерева Т' путем добавления |e_o \ v_o| новых вершин и соединения их с вершиной v_o.

Гиперграф Н, изображенный на рис. 71.1, удовлетворяет условиям теоремы 71.1, поэтому существует его реализация деревом; это дерево G' представлено на том же рисунке.

Говорят, что гиперграф Н удовлетворяет ослабленному условию Хелли, если для любого множества попарно смежных ребер {e₁, e₂, ..., e_k } гиперграфа Н существуют две такие вершины и, v € VH, что е_i ∩ (и, v) ≠ ¢ для каждого i=1,k.

Следующие две теоремы приведем без доказательства.

Теорема 71.2. Если гиперграф Н удовлетворяет ослабленному условию Хелли и его реберный граф L(H)

триангу линованный, то существует реализация Н планарным графом.

Теорема 71.3. Если реберный граф гиперграфа В является планарным, то существует реализация Н планарным графом.

В рассмотренных выше реализациях одно и то же ребро реализующего графа может участвовать в реализации нескольких ребер гиперграфа. Естественно возникают задачи построения таких реализаций гиперграфа, в которых это запрещено.

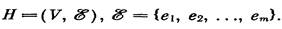Пусть задан гиперграф

строгой реализацией гиперграфа Н называется любой граф G, удовлетворяющий следующим условиям:

1) VG = VH;

2) существует такое разбиение множества EG ребер графа G на подмножества E₁, E₂ ,…, E_m, что граф, индуцированный множеством E_i ,является реализацией ребра E_i гиперграфа Н.

Конечно, всякая строгая реализация гиперграфа является его реализацией.

На рис. 71.1 граф G" является строгой реализацией гиперграфа Н, а граф G' не является такой реализацией (почему?). Следующий пример показывает, что гиперграф может не иметь строгой реализации.

Пример. Рассмотрим гиперграф Н=(V, E), где V= {v₁,v₂,v₃,v₄},E = {{v₁,v₂,v₃}, {v₁,v₂,v₄},{v₁,v₃,v₃₄} ,{v₂,v₃,v₄}}. Если бы существовала строгая реализация этого гиперграфа, то она должна была бы иметь не менее 2 * 4 = 8 ребер, что невозможно для графа с четырьмя вершинами.

Чтобы сформулировать критерий существования строгой реализации гиперграфа Н=(V, E), E = {е₁,е₂,...,е_т}, воспользуемся одним фактом из теории матроидов.

Обозначим через G_i полный граф с множеством вершин е_i и положим Е = Е(Н)=UEG_i. Рассмотрим

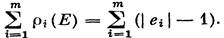на множестве Е т таких матроидов М₁, М₂, ..., М_т, что M_i — циклический матроид графа G_i Пусть p_i— ранговая функция матроида M_i(i =1, m). Ясно, что p_i(E)=| e_i | — 1. Очевидно, что существование строгой реализации гиперграфа Н=(V, E) равносильно существованию попарно пепересекающихся баз В_i € M_i (i =1, m). Последнее условие, в свою очередь, выполняется тогда и только тогда,когда ранг матроида М =U M_i не меньше, чем

Теперь, применив теорему 24.1,получим следующий критерий существования строгой реализации.

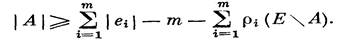Теорема 71.4. Строгая реализация гиперграфа Н=(V, E) с m ребрами существует тогда и только тогда, когда для любого множества А € Е выполняется неравенство

Отметим, что для построения строгой реализации гиперграфа существует эффективный алгоритм.

1 23

Дата добавления: 2019-07-26; просмотров: 440;