Лекция 9. Динамика твердого тела. 4 страница

Плоское качение цилиндра без проскальзывания по негладкой плоскости y = 0 .

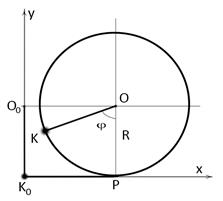
В общем случае положение твердого тела определяется шестью степенями свободы – тремя координатами полюса в теле, и тремя углами между осями неподвижной и подвижной осями координат. В данном примере шесть параметров связаны пятью уравнениями связей

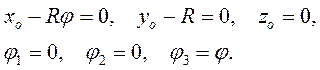
Условие качения без проскальзывания выражает первое уравнение. В нем для некоторой точки К на поверхности цилиндра принято, что в начальном положении она (К₀) находилась в начале координат. Цилиндр имеет одну степень свободы.

Ускорение точек твердого тела. Угловое ускорение тела.

Продифференцируем по времени формулу (7.5):

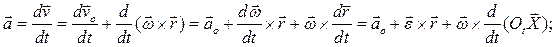
Здесь вектор 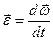называется угловым ускорением твердого тела. Итак,

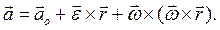(7.8)

Формула (7.8) задает поле ускорений в теле, то есть каждому вектору 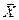(или его образу 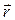) сопоставляется вектор ускорения точки 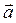. Аналогично, формула (7.5) задает поле скоростей точек твердого тела.

Абсолютная и относительная производные вектора, заданного в подвижной системе координат.

Пусть некоторый вектор 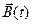задан в подвижном базисе:

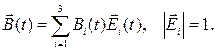
Определения.

Относительная производная вектора 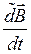, заданного в подвижном базисе, есть

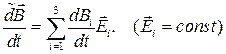(7.9)

Абсолютная производная вектора, заданного в подвижном базисе, 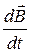, есть

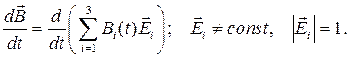(7.10)

Тогда связь между ними в подвижном базисе имеет вид:

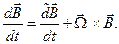(7.11)

Здесь 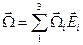есть угловая скорость вращения подвижного базиса.

Доказательство.

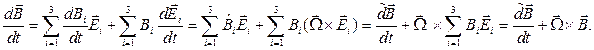
Если вектор 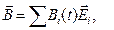заданный в подвижном базисе, перезаписан в неподвижный базис, то абсолютная производная этого вектора 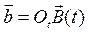в неподвижном базисе имеет вид:

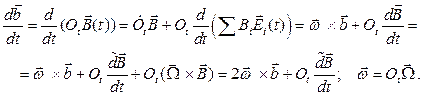(7.12)

Лекция 8.Кинематика сложного движения точки и твердого тела.

Представить движение как сложное – это значит представить абсолютное движение как два движения – относительное плюс переносное.

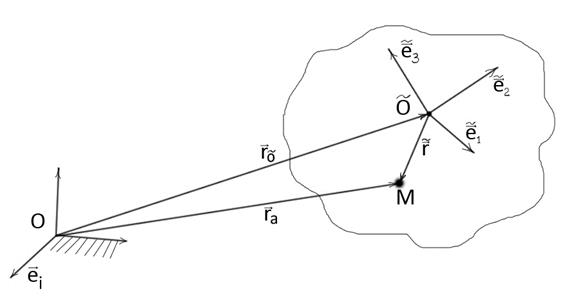
Сложное движение точки.

Введем две системы отсчета: неподвижную (absolute) - с системой координат 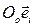и подвижную - с системой координат .

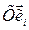Определения. 1. Движение точки M по отношению к подвижной системе отсчета называется относительным (relative):

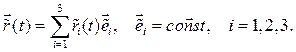(8.1)

Относительная скорость и относительное ускорение есть:

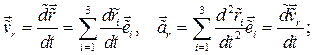(8.2)

2. В каждый данныймомент времени переносным (entraine) движением точки M называется движение той точки подвижной системы отсчета по отношению к неподвижной системе отсчета, в которой движущаяся точка в данный момент находится.

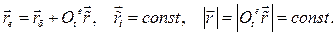(8.3)

Переносная скорость, переносное ускорение есть:

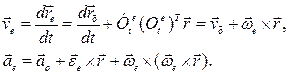(8.4)

Здесь 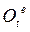есть матрица переносного вращения подвижной системы отсчета.

3. Абсолютным (absolute) движением называется движение точки по отношению к неподвижной системе координат:

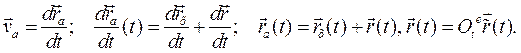(8.5)

Абсолютная скорость, абсолютное ускорение точки есть:

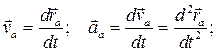(8.6)

Теоремы сложения скоростей и ускорений в сложном движении точки.

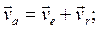(8.7)

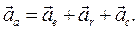(8.8)

где последнее слагаемое есть ускорение Кориолиса

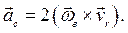(8.9)

Доказательство. Сложное движение точки есть сумма двух движений:

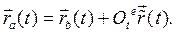
Теоремы докажем в неподвижном базисе.

Переносные характеристики уже записаны в неподвижном базисе.

Относительные характеристики, заданные в подвижном базисе, перезапишем в неподвижном базисе. Тогда по (7.12) получим:

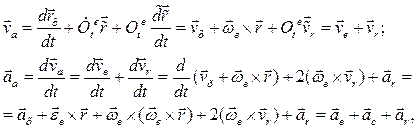
где

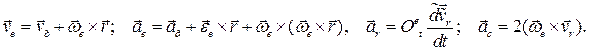
Сложное движение твердого тела.

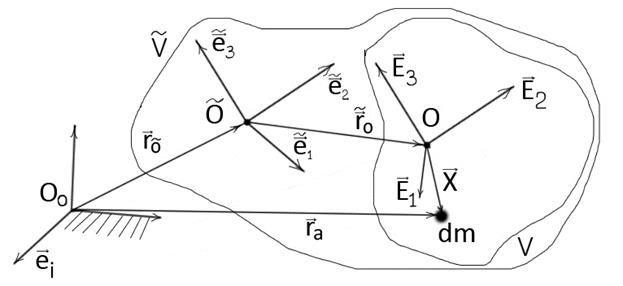
В тех случаях, когда абсолютное движение твердого тела можно представить, как два движения, говорят о представлении движения твердого тела как сложное движение.

Чтобы задать абсолютное движение, введем неподвижную, абсолютную систему координат 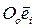. Тогда абсолютное движение тела определяется движением полюса О и матрицей абсолютного вращения .

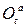Введем подвижную систему координат 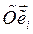, по отношению которой относительное движение тела определяется относительным движением 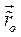полюса О и матрицей относительного вращения 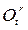, а переносное движение задается вектором 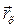и матрицей .

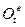Наконец, для индивидуализации точек тела, как и раньше, задана в теле система координат 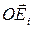, жестко связанная с телом.

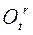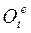Исследуем только вращательные части относительного и переносного вращений, заданные матрицами и соответственно, игнорируя при этом все поступательные движения. Это значит, что начала всех систем координат совпадают, и точка О есть неподвижная точка тела. Тогда абсолютное вращение тела есть композиция двух последовательных аффинных преобразований с ортогональными матрицами. Поэтому 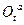определяется как произведение матриц 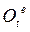и :

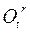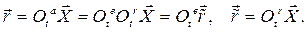
Абсолютная скорость любой точки тела 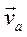есть для сферического движения

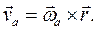
Здесь вектор 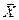последовательно перезаписывается сначала в подвижном базисе как 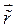, а потом в неподвижном как .

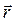Представляя движение тела как сложное, вычислим скорость точки 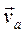так:

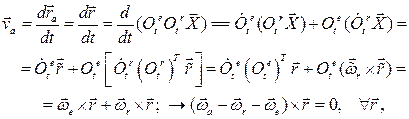
Здесь 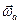, , 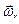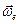есть угловые скорости абсолютного, относительного и переносного вращений соответственно.

В результате получаем теорему о сложении векторов угловых скоростей относительного 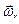и переносного 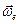вращений:

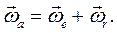(8.10)

Дифференцируя (8.10) по времени, докажем теорему о сложении угловых ускорений твердого тела в сложном движении:

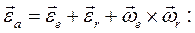(8.11)

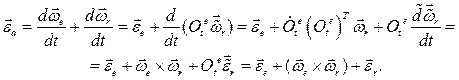
Здесь 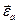, , 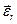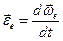и 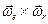есть абсолютное, относительное и добавочное угловые ускорения.

Лекция 9. Динамика твердого тела.

Инерционные характеристики абсолютно твердого тела.

Масса тела, а также пространственное распределение элементарных масс в теле влияют на способность тела препятствовать ускорению или замедлению движения тела при его поступательном или вращательном движениях. Эти свойства называется инерционностью тела.

Определения.

Центр масс С есть постоянная в теле точка в подвижной системе координат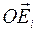

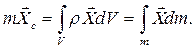(9.1)

Здесь вектор 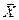определяет в теле положение элементарной массы тела 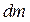, - её элементарный объем. Удельная массовая плотность 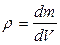. Масса тела есть m .

В неподвижной системе координат центр масс имеет положение

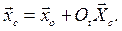
При движении тела центр масс движется и имеет в неподвижной системе координат скорость 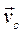и ускорение :

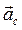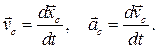(9.2)

Импульс абсолютно твердого тела есть вектор

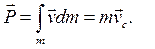(9.3)

Момент импульса телаотносительно неподвижной точки 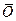есть вектор:

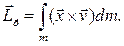(9.4)

Кинетическая энергия твердого тела есть скаляр

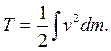(9.5)

Теоремы динамики твердого тела.

Теорема о движении центра масс:

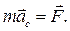(9.6)

Теорема об изменении импульса тела :

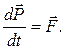(9.7)

Теорема об изменении момента импульса тела :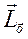

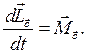(9.8)

Теорема об изменении кинетической энергии:

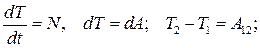(9.9)

Все обозначения в формулах (9.6) – (9.9) такие же, как в соответствующих теоремах для системы точек (6.3) – (6.11). Заметим, что для одного тела все силы есть внешние.

Оператор инерции твердого тела. Осевые и центробежные моменты инерции.

Хотя оператор инерции не зависит от движения тела, однако некоторые динамические характеристики движения тела выражаются через оператор инерции.

Например, момент импульса твердого тела относительно неподвижной в теле точки О вычисляется по формуле:

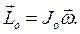(9.10)

Доказательство:

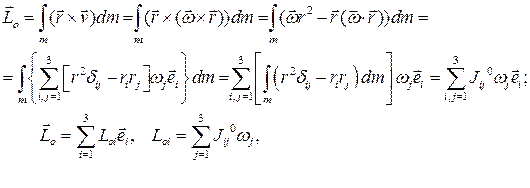
Симметричный линейный оператор, который называется операторинерции для точки 0

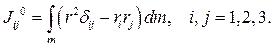(9.11)

сопоставляет вектору угловой скорости 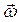вектор момента импульса 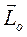. Матрица оператора инерции в подвижном базисе имеет постоянные элементы. Диагональные элементы называются осевые моменты инерции ,

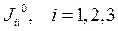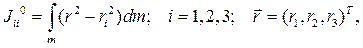(9.12)

а недиагональные элементы - центробежные моменты инерции :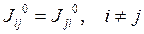

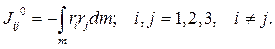(9.13)

Например, обозначив 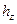расстояние от элементарной массы dm до оси Оz , видим, что

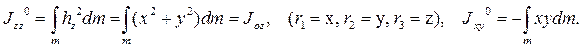
Центробежные моменты инерции равны нулю, если в качестве подвижных осей выбраны собственные векторы оператора инерции. Тогда положительные собственные числа этого оператора есть осевые моменты инерции. Матрица оператора инерции диагональна.

Формула Гюйгенса - Штейнера показывает связь между осевыми моментами инерции относительно двух параллельных осей, одна из которых проходит через центр масс телаточку С:

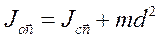(9.14)

Здесь d - расстояние между осями. Вектор 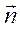есть направляющий вектор параллельных осей.

Доказательство:

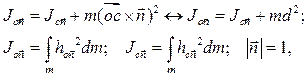
Вычисление кинетической энергии твердого тела. Формула Кенига.

Рассматриваем движение твердого тела как сложное. За подвижную систему координат выбираем систему координат Кенига 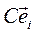с началом в центре масс С и базисом, который движется поступательно. Тогда относительная скорость всех точек тела есть 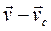, а переносная скорость точек есть .

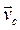Тогда кинетическую энергию твердого тела можно представить как сумму двух слагаемых (формула Кенига):

Т = 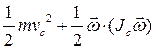. (9.15)

Докажем эту формулу.

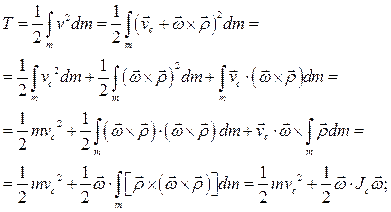
Для плоского движения тела из (9.15) получим:

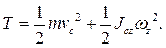(9.16)

Для сферического движения с неподвижной точкой 0

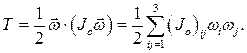(9.17)

а в главных подвижных осях инерции для неподвижной точки 0 получим формулу:

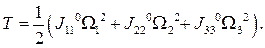(9.18)

Задача 9.1. Доказать, что для тела, которое вращается вокруг неподвижной оси 0z, кинетическая энергия точки вычисляется по формуле:

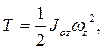(9.19)

Задача 9.2. Доказать, что в плоском непоступательном движении кинетическая энергия может быть вычислена по формуле:

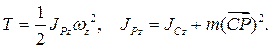(9.20)

Здесь 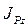есть осевой момент инерции тела относительно оси мгновенной оси вращения Pz, проходящей через мгновенный центр скоростей Р плоской фигуры, перпендикулярно этой фигуре.

Лекция 10.Дифференциальные уравнения движения твердого тела.

Произвольное движение твердого тела определяют шесть параметров – три координаты полюса и три угла, через которые можно выразить элементы матрицы вращения. Поэтому, взяв за полюс центр масс твердого тела С, шесть скалярных уравнений (два векторных уравнения)

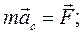(10.1)

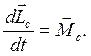(10.2)

решают любую задачу динамики твердого тела.

Здесь 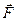и 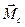есть главный вектор всех сил и главный момент всех сил относительно центра масс. Уравнения (10.1) и (10.2) называются дифференциальные уравнения движения твердого тела.

При решении задач динамики к (10.1) и (10.2) добавляют уравнения связей.

Дифференциальное уравнение вращения тела вокруг неподвижной оси.

Так как в этом случае тело имеет одну степень свободы, и угол 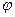в матрице вращения подвижных осей координат по отношению к неподвижным осям определяет движение тела, то дифференциальным уравнением вращения твердого тела вокруг неподвижной оси является проекция теоремы об изменении момента импульса тела на ось вращения Оz .

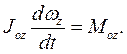(10.3)

Здесь 0 есть любая неподвижная точка на оси вращения.

Скалярные уравнения (10.1), (10.2) удобно записывать в подвижном базисе ОЕ_i (тогда элементы матрицы оператора инерции постоянны) и служат для нахождения сил реакций связей.

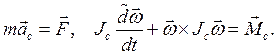
В последнем уравнении взята относительная производная 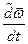от вектора угловой скорости (смотри формулы (7.11), (7.12)).

Задача 10.1. Проверить, что если подвижную ось 0х провести через центр масс тела, а ось Оz – вдоль оси вращения тела 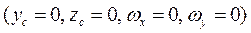, то дифференциальные уравнения движения твердого тела (10.1), (10.2) для случая его вращения вокруг неподвижной оси 0z имеют в подвижном базисе следующий вид:

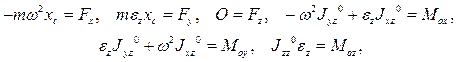(10.4)

Здесь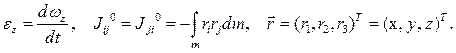

Главный вектор 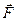и главные моменты сил относительно осе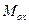й и 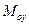включают компоненты неизвестных сил реакций связей. Аксиомы сил реакций оси вращения задаются так, чтобы компоненты неизвестных сил реакций оси и их моментов не содержали больше пяти неизвестных.

Дифференциальные уравнения плоского движения твердого тела.

Плоское движение тела определяется тремя параметрами: двумя координатами полюса 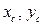и углом поворота 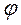, через который выражаются все элементы матрицы вращения .

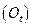Поэтому три скалярных дифференциальных уравнения плоского движения тела служат для нахождения движения тела и некоторых сил реакций связей и имеют вид:

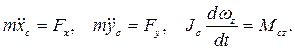(10.5)

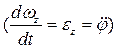
Из остальных уравнений движения

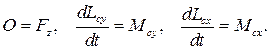
находят неизвестные силы реакций, либо записывают ограничения на активные силы и их моменты, чтобы движение тела было плоским.

Дифференциальные уравнения сферического движения твердого тела.

Так как тело с неподвижной точкой имеет три степени свободы, то дифференциальные уравнения сферического движения есть теорема об изменении момента импульса тела относительно неподвижной точки О (10.2), записанного в подвижной базисе ОЕ_i (тогда элементы матрицы оператора инерции 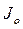есть постоянные числа):

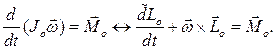(10.6)

Здесь нужно использовать формулу (7.11) связи абсолютной и относительной производной от вектора, записанного в подвижной системе координат. Если уравнения движения проинтегрированы, то ускорение центра масс есть

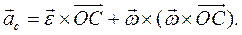
и из (10.1) находят связь активных сил и сил реакций.

Задача 10. 2. Написать уравнения движения в главных подвижных осях оператора инерции относительно неподвижной точки. Обозначить: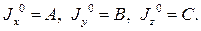

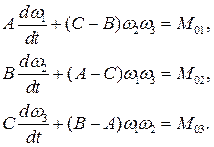(10.7)

Эти уравнения называются динамические уравнения Эйлера.

Покой твердого тела.

Тело находится в равновесии, если любая его точка не имеет ускорения на некотором интервале времени его движения. Покой есть частный случай равновесия, когда и ускорения, и скорости всех точек тела равны нулю на конечном интервале времени его движения.

Из уравнений движения (10.1) и (10.2) следуют условия на силы для равновесия твердого тела:

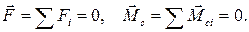(10.8)

Эти условия, записанные в проекциях на любой неподвижный базис, есть уравнения равновесия для нахождения неизвестных проекций сил реакций тела по известным активным силам. При этом аксиомы сил формулируются так, чтобы их число было не больше шести (для пространственной системы сил).

Для других систем сил число неизвестных и число условий равновесия меньше шести.

Если условия равновесия необходимы для равновесия тела, то достаточными условиями равновесия могут быть следующие условия:

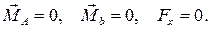(10.9)

Здесь точки А и В есть любые две неподвижные точки, а ось Оx есть любая ось, не перпендикулярная вектору .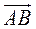

Для вывода условий (10.9), достаточных для равновесия тела, можно использовать связь между главными моментами системы сил относительно двух разных полюсов (А и В) и главным вектором системы сил:

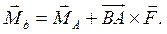(10.10)

Задача 10.3. Доказать достаточность условий (10.9) для равновесия тела.

Задача 10.4. Проверить, что условия

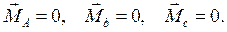(10.11)

являются достаточными условиями равновесия твердого тела. Здесь А , В и С есть три неподвижных точки, не лежащие на одной прямой.

Если в равновесии находится система твердых тел, то уравнения равновесия (10.8) можно записать как для каждого тела системы, так и для любого числа тел системы (любой подсистемы тел). В последнем случае в уравнениях равновесия отсутствуют внутренние силы подсистемы. Независимость полученной системы уравнений необходимо проверять.