Лекция 9. Динамика твердого тела. 1 страница
Основные понятия и аксиомы механики Ньютона.
Механика есть наука о механических движениях и взаимодействиях материальных тел.
В курсе «Теоретическая механика» изучаются классические математические модели реальных тел: материальная точка, система материальных точек, абсолютно твердое тело.
Основные понятия механики. Пространство, время, система отсчета, система координат. Масса.
Пространство, в котором находятся материальные тела, моделируется как трехмерное и эвклидово, а время как одномерное. Масса тела, как мера его инертности, постоянна. 
Положение точки. В выбранной декартовой системе координат положение точки определяется упорядоченной тройкой действительных чисел x, y, z , координат точки (вектором 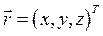 ).
).
Движение точки есть последовательное во времени изменение ее положения по отношению к выбранной системе отсчета.
Вдекартовых координатах движение задается дважды дифференцируемым отображением 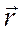 :
: 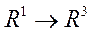 , то есть
, то есть 
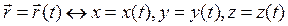 , t
, t 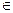
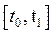 (1.1)
(1.1)
Скорость и ускорение точки:
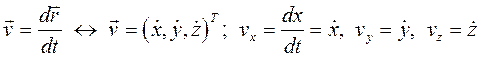
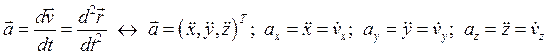 (1.2)
(1.2)
Связи. Уравнения связей. Если тело при движении контактирует с другими телами, то его положение в пространстве не может быть произвольным. Ограничения (связи) на положение тела записывают в виде уравнений геометрических связей.
Три координаты точки связаны уравнениями связей. Поэтому число независимых координат точки меньше трех. Число независимых координат точки (обобщенных координат) называют ее числом степеней свободы.Ограничения на скорость и ускорение точки представляют в виде кинематических уравнений связей, которые получают из геометрических уравнений их дифференцированием по времени.
Пример 1. Математический маятник есть точка, подвешенная на нити, имеющей постоянную длину 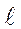 , которая движется в вертикальной плоскости z = 0 по части окружности. Уравнения геометрических связей:
, которая движется в вертикальной плоскости z = 0 по части окружности. Уравнения геометрических связей: 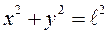 ,
,  z = 0. Три координаты связаны двумя уравнениями. Поэтому имеется одна независимая координата. Точка имеет одну степень свободы. Уравнения кинематических связей точки маятника:
z = 0. Три координаты связаны двумя уравнениями. Поэтому имеется одна независимая координата. Точка имеет одну степень свободы. Уравнения кинематических связей точки маятника:
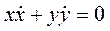 ,
, 
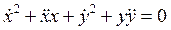 .
.  (1.3)
(1.3)
Взаимодействие тел: силы действия и противодействия.
.Механические взаимодействия тел вызывают движение этих тел или деформируют их. Сила – мера взаимодействия тел есть вектор. Силу действия называют активной силой, силу противодействия – силой реакции. Для некоторых взаимодействий тел свойства сил взаимодействий формулируют в аксиомах сил и их моментов.
Механика Ньютона. Модель «материальная точка».
Аксиомы (принципы) механики Ньютона – три закона Ньютона.
1. Первый закон Ньютона. Существуют системы отсчета (инерциальные системы), в которых изолированная материальная точка (равнодействующая всех сил ее взаимодействий с другими телами равна нулю), сохраняет покой или движется равномерно и прямолинейно.
2. Второй закон Ньютона (в векторной форме и в декартовых координатах):
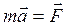 ,
,
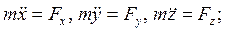 (1.4)
(1.4)
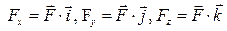 .
.
3. Третий закон Ньютона. Для двух взаимодействующих тел сила действия равна по величине и противоположна по направлению силе противодействия. Векторы сил имеют общую линию действия.
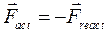 . (1.5)
. (1.5)
Уравнения (1.4) есть дифференциальные уравнения движения точки в декартовых координатах.
Основные задачи динамики материальной точки.
Прямая задача: нахождение сил по известному движению (или его характеристикам).
Пример прямой задачи. Снаряд массой m вылетает из ствола орудия на поверхности Земли со скоростью v0 под углом α к горизонту. Движение снаряда в декартовых координатах известно:
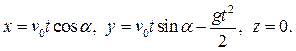
Здесь 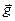 есть постоянное ускорение свободного падения точки у Земли. Какая сила
есть постоянное ускорение свободного падения точки у Земли. Какая сила 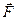 вызвала это движение?
вызвала это движение?
Обратная задача. Нахождение движения по известным силам взаимодействий известному начальному состоянию.
Пример обратной задачи. Снаряд, моделируемый как материальная точка, притягивается к Земле с постоянной силой притяжения к Земле (силой тяжести 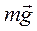 ). Найти движение снаряда, если в начальный момент времени его выпустили с Земли со скоростью v0 под углом α к горизонту.
). Найти движение снаряда, если в начальный момент времени его выпустили с Земли со скоростью v0 под углом α к горизонту.
В этом случае движение точки есть решение дифференциальных уравнений (1.4), которое однозначно определяется начальным состоянием точки – начальным положением и начальной скоростью точки.
Задача 1.1. Найти траекторию снаряда, дальность L егополета до Земли, максимальную высоту H подъема снаряда, а также время T его полного полета.
Задача 1.2. В условиях предыдущей задачи, найти время полета снаряда, если он упал в яму глубиной h.
Задача 1.3. Найти силу реакции T нити математического маятника в нижнем положении точки на окружности 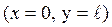 , если в этом положении скорость точки равна
, если в этом положении скорость точки равна 
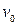 . Ось 0y направлена по вертикали вниз.
. Ось 0y направлена по вертикали вниз.
Решение. Уравнения связей (1.3) справедливы для любого положения точки на окружности. В нижнем положении точки оно принимает вид:

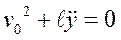 .
.
Из второго уравнения закона Ньютона (1.4) получаем:
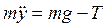 ,
,
откуда, используя предыдущее уравнение, получаем значение силы реакции в нижнем положении маятника:
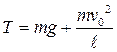 .
.
Задача 1.4. Капсула спускаемого аппарата с космонавтом на большой высоте H над Землей имела скорость vН . Какова скорость vЗ снаряда у поверхности Земли, если пренебречь вращением капсулы и сопротивлением воздуха. Учесть гравитационную силу притяжения снаряда к Земле, обратно пропорциональную квадрату расстояния от снаряда до центра «неподвижной» Земли. Радиус Земли равен R . На поверхности Земли сила притяжения равна mg .
Решение. Выберем ось 0x от центра 0 Земли вдоль прямолинейной траектории движения космонавта (как точки). Проекция на ось 0x силы притяжения 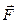 , с учетом ее значения на Земле
, с учетом ее значения на Земле 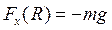 , равна
, равна
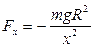 .
.
Второй закон Ньютона в проекции на ось 0x имеет вид:
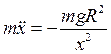 . (1.6)
. (1.6)
В обратной задаче динамики требуется проинтегрировать уравнение движения с учетом начального состояния. За независимые параметры примем положение и скорость точки, тем более что начальные значения этих параметров заданы. Так как
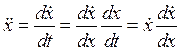 ,
,
то, разделяя в уравнении (1.6) переменные x, 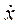 , получим:
, получим:
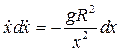 , (1.7)
, (1.7)
Для решения задачи достаточно проинтегрировать (1.7) один раз. Получаем:
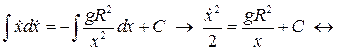
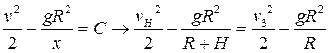 .
.
Интегрирование этого уравнения дает следующее значение скорости космонавта при подлете к Земле:
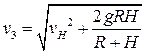 .
.
Лекция 2.Движение вдоль траектории. Скорость и ускорение точки в проекциях на естественный ортонормированный базис.
Траектория точки есть геометрическое место всех последовательных положений точки при ее движении. Пусть это есть некоторая гладкая кривая линия в 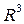 .
.
Пусть траекторияизвестна и задана в параметрической форме:
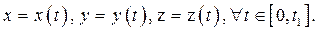 (2.1)
(2.1)
В таком случае, в силу уравнений (3.1), как уравнений геометрических связей, точка имеет один независимый параметр t (одну степень свободы).
Выберем, однако, вместо t другой независимый параметр - дуговую координату s - расстояние вдоль кривой от некоторого начального положения точки O на траектории до ее текущего положения. При движении точки по траектории 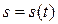 и
и
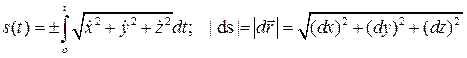 (2.2)
(2.2)
Далее при записи уравнения траектории примем в качестве независимого параметра дуговую координату s:
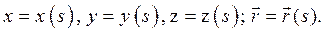 (2.3)
(2.3)
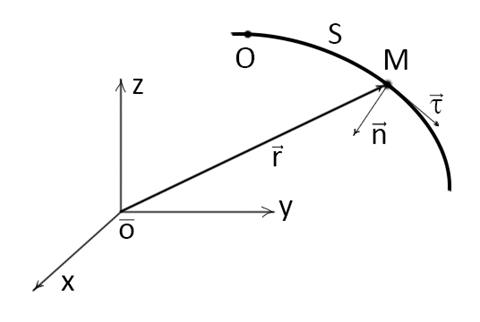
Касательный к траектории вектор 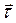 определим следующим образом:
определим следующим образом:
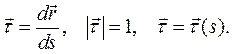 (2.4)
(2.4)
Вектор главной нормали 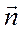 перпендикулярен к вектору
перпендикулярен к вектору 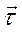 и определяется следующим образом:
и определяется следующим образом:
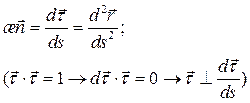
 (2.5)
(2.5)
Величина 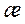
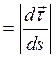 называется кривизной кривой в точке М, а величина
называется кривизной кривой в точке М, а величина 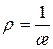 называется радиусом кривизны.
называется радиусом кривизны.
В каждой точке траектории три единичных вектора 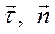 и
и 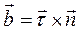 взаимно перпендикулярны и образуют естественный ортонормированный базис, ориентация векторов которого определяется видом траектории и положением точки М на траектории.
взаимно перпендикулярны и образуют естественный ортонормированный базис, ориентация векторов которого определяется видом траектории и положением точки М на траектории.
Движение точки в естественной форме
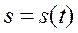 (2.6)
(2.6)
Скорость точки 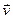 направлена параллельно вектору
направлена параллельно вектору 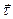 :
:
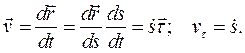 (2.7)
(2.7)
а её проекция на ось 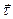 равна:
равна:
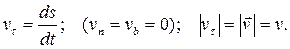
Ускорение точки 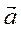 раскладывается по естественному базису так:
раскладывается по естественному базису так:
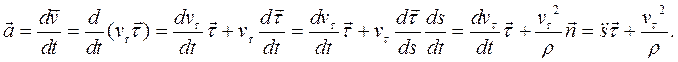
Компоненты вектора ускорения называются так: касательное 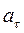 , нормальное
, нормальное 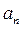 и бинормальное
и бинормальное 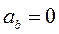 ускорения.
ускорения.
Окончательно:
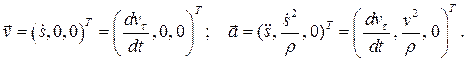 (2.8)
(2.8)
Закон Ньютона 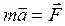 в проекциях на естественный базис запишем в виде:
в проекциях на естественный базис запишем в виде:
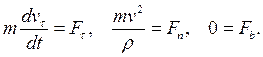 (2.9)
(2.9)
Если траектория точки есть окружность с радиусом R , то кривизна окружности равна, по определению, радиусу окружности, и поэтому нормальное ускорение точки есть
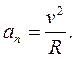 (2.10)
(2.10)
Задача 2.1. Материальная точка массы m движется в поле силы тяжести по гладкой неподвижной окружности радиуса R в вертикальной плоскости. Написать дифференциальное уравнение движения точки. Дуговую координату s отсчитывать от её нижнего положения. Найти скорость точки в любом её положении, если в нижнем положении она равна v0 . При какой начальной скорости v0 0 точка пройдет всю окружность?
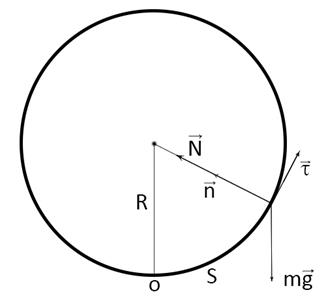
Решение. Закон Ньютона в проекции на касательный вектор к траектории имеет вид:
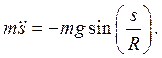 (2.11)
(2.11)
Это есть дифференциальное уравнение движения математического маятника. Для того, чтобы найти движение, нужно интегрировать это уравнение. Однако его нельзя проинтегрировать в элементарных функциях. Решение в эллиптических функциях показывает, что движение точки периодическое, но период колебаний не есть постоянная величина.
Для нахождения начальной скорости, при которой точка пройдет всю окружность, используем закон сохранения механической энергии, который можно получить интегрированием (3.11) один раз,
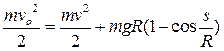
и условие того, что в верхней точке траектории скорость больше нуля:
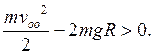
Ответ: 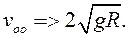
Задача 2.2. Материальная точка массы m движется по гладкой неподвижной кривой в виде ветви циклоиды в вертикальной плоскости в поле силы тяжести mg.Уравнение траектории в параметрической форме имеет вид:
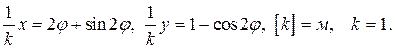
При движении точки по траектории 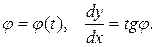
Для любого положения точки М на циклоиде угол 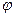 есть угол между касательной к кривой и горизонталью. Ось Оx горизонтальна, а Оy направлена вертикально вверх. Выбрав за начало отсчета дуговой координаты s низшее положение точки М на траектории, найти движение точки в естественной форме s = s(t). Найти также силу реакции кривой R для любого положения s точки на циклоиде, если в начале координат точка имеет минимальную скорость.
есть угол между касательной к кривой и горизонталью. Ось Оx горизонтальна, а Оy направлена вертикально вверх. Выбрав за начало отсчета дуговой координаты s низшее положение точки М на траектории, найти движение точки в естественной форме s = s(t). Найти также силу реакции кривой R для любого положения s точки на циклоиде, если в начале координат точка имеет минимальную скорость.
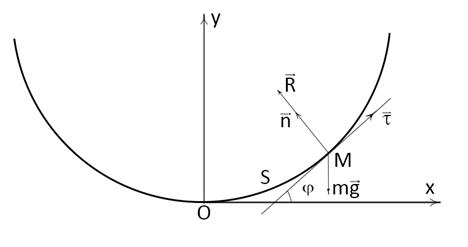
Решение. Определим векторы естественного ортонормированного базиса 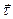 и
и 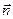 :
:
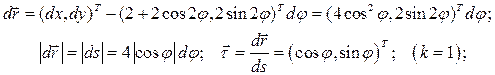
Кривизна кривой 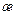 и радиус кривизны
и радиус кривизны 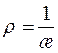 имеют вид:
имеют вид:
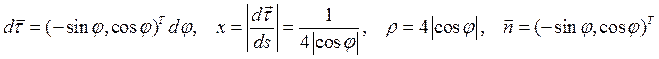
Длина дуговой координаты s, отсчитываемой из низшего положения на траектории, равна:
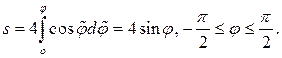
Закон Ньютона в естественном базисе (2.9) запишем в виде:
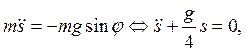
откуда получаем движение точки в естественном виде:
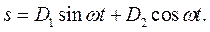
Это решение есть гармоническое колебание с постоянной круговой частотой колебаний 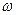
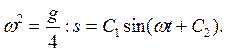
и с постоянным периодом колебаний
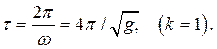
Тяжелую точку в её движении по циклоиде называют циклоидальным маятником.
Сила реакции циклоиды 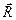 находится из закона Ньютона (2.9) в проекции на нормаль к траектории:
находится из закона Ньютона (2.9) в проекции на нормаль к траектории:
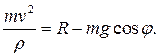
Скорость точки находится из закона сохранения механической энергии:
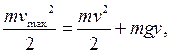
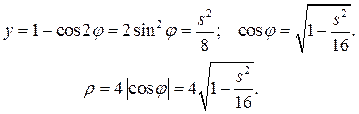
Ответ: 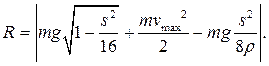
Лекция 3.Криволинейные системы координат.
Декартовой системой координат в R3 называется совокупность точки О, начала координат, и трех векторов 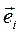 I =1, 2, 3. -- векторов ортонормированного базиса.
I =1, 2, 3. -- векторов ортонормированного базиса.
Определение. Каждой точке 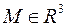 с координатами
с координатами 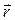 = (x, y, z)T сопоставим три упорядоченных числа k1 , k2 , k3, по некоторому правилу:
= (x, y, z)T сопоставим три упорядоченных числа k1 , k2 , k3, по некоторому правилу:
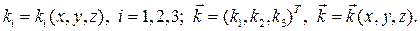 (3.1)
(3.1)
Назовем ki , i = 1, 2 ,3, криволинейными координатами точки М. Функции (3.1) взаимно однозначны и непрерывно дифференцируемы по всем координатам и имеют обратные функции в некоторой области взаимной однозначности
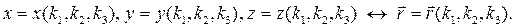 (3.2)
(3.2)
Определение. Три вектора
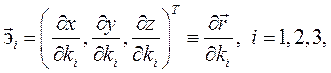
называются базисом криволинейных координат в любой точке М из области определения криволинейных координат. В ней функции (3.2) взаимно однозначны и взаимно непрерывно дифференцируемы. Компоненты векторов базиса записаны в декартовом базисе. Каждый вектор базиса касается соответствующей координатной линии, вдоль которой в (3.2) изменяется только одна координата, а две другие фиксированы. Длины векторов базиса hi (коэффициенты Ламе) могут быть для разных точек М различными и вычисляются по формулам:
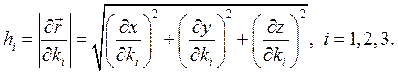 (3.3)
(3.3)
Координатные поверхности, проходящие через точку М, определяются уравнениями
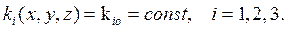
При этом координатные поверхности пересекаются по координатным линиям, проходящим через точку М.
Базис 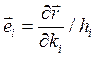 единичный, нормированный базис.
единичный, нормированный базис.
Криволинейная система координат называется ортогональной системой координат, если векторы базиса ортогональны:
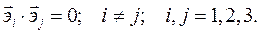
Ортонормированный базис 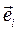 ортогональной системы координат удовлетворяет условию:
ортогональной системы координат удовлетворяет условию:
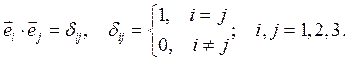
Цилиндрическая ортогональная система координат.
Прямое отображение K: 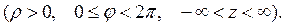
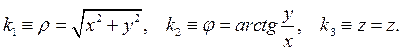 (3.4)
(3.4)
Обратное отображение 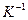 :
:
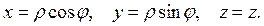 (3.5)
(3.5)
Коэффициенты Ламе: 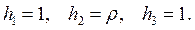
Ортонормированный базис 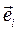 в разложении по декартовому базису имеет вид:
в разложении по декартовому базису имеет вид:
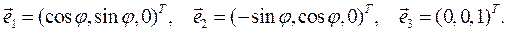 (3.6)
(3.6)
Сферическая ортогональная система координат.
Прямое отображение: 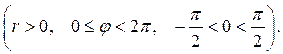
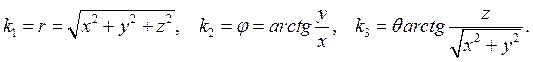
Обратное отображение:
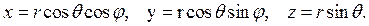
Коэффициенты Ламе: 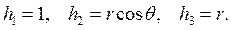
Скорость и ускорение точки в ортонормированном базисе криволинейной системы координат определяются по движению точки в криволинейных координатах
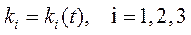
следующим образом:
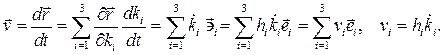 (3.7)
(3.7)
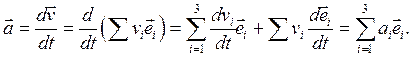 (3.8)
(3.8)
Компоненты 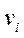 вектора скорости и компоненты
вектора скорости и компоненты 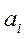 вектора ускорения в ортонормированном базисе
вектора ускорения в ортонормированном базисе 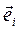 криволинейных координат называются физическими компонентами и имеют обычную физическую размерность.
криволинейных координат называются физическими компонентами и имеют обычную физическую размерность.
Пример вычисления физических компонент векторов скорости и ускорения в цилиндрических координатах.
Физические компоненты вектора скорости имеют по (3.7) значения:
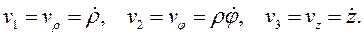 (3.9)
(3.9)
Для компонент вектора ускорения вычислим сначала 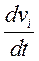 в базисе
в базисе 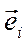 ,
,
а затем посчитаем векторы 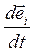 . Так как векторы
. Так как векторы 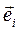 записаны в декартовом базисе в виде (3.6), то получаем в этом базисе:
записаны в декартовом базисе в виде (3.6), то получаем в этом базисе:
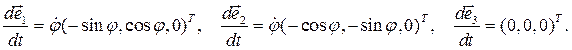
Сравнивая эти векторы с векторами (2.6), получаем:
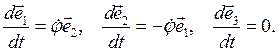
Окончательно, по формуле (3.8)
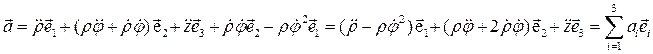
и тогда
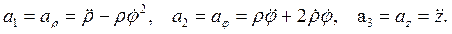 (3.10)
(3.10)
Полярная система координат.
Если в цилиндрических координатах положить z = 0 , то система координат называется полярной системой координат. Она описывает движение точки в одной плоскости. Для нее физические компоненты векторов скорости и ускорения имеют вид 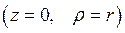 :
:
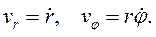 (3.11)
(3.11)
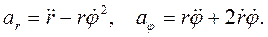 (3.12)
(3.12)
Задача 3.1. Вычислить физические компоненты векторов скорости и ускорения в сферических координатах.
Решение.
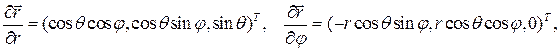
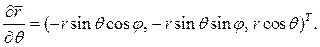
Коэффициенты Ламе вычислим по (2.3): 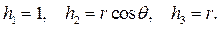
Ортонормированный базис 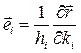 , записанный в декартовом базисе, имеет вид:
, записанный в декартовом базисе, имеет вид:
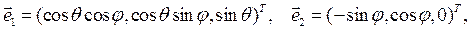
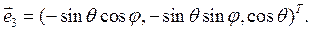
Физические компоненты вектора скорости 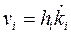 есть:
есть:
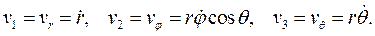
Вычислим вектор ускорения точки 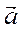 :
:
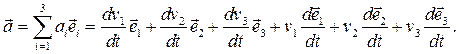 (3.13)
(3.13)
Сначала вычисляются скалярные величины 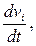 а затем - векторы
а затем - векторы 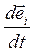 .
.
Покажем, что векторы 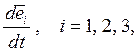 перпендикулярны к соответствующим векторам
перпендикулярны к соответствующим векторам 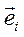 . Действительно:
. Действительно:
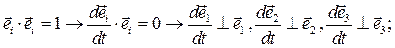
Отсюда можно сделать вывод о том, что каждый вектор 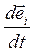 раскладывается по двум векторам базиса
раскладывается по двум векторам базиса 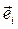 с номерами, не совпадающими с номером i .
с номерами, не совпадающими с номером i .
Для вектора 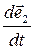 можно получить, что:
можно получить, что:
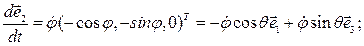
Дата добавления: 2019-07-26; просмотров: 802;
