Лекция 9. Динамика твердого тела. 3 страница

Из формулы (5.13) первая космическая скорость равна

,

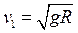а из формулы (5.14) вторая космическая скорость равна

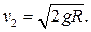
Траектории планет Солнечной системы. Законы Кеплера.

Если принять за неподвижный центр притяжения Солнце, то гравитационная сила притяжение записывается так:

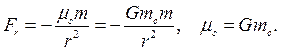(5.12)

где постоянная Гаусса Солнца 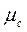записывается через гравитационную постоянную Солнечной системы G и массу Солнца 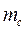. Траектории планет – эллипсы, для которых Солнце находится в фокусе эллипса. Угол φ отсчитывается от перигелия – минимального расстояния 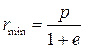планет от Солнца. Это первый закон Кеплера.

Из (5.1) и (5.2) вытекает второй закон Кеплера, выраженный через секторную скорость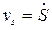

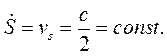(5.13)

Здесь S(t) - площадь, заметаемая вектором 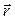за время t .

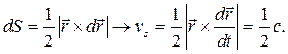
Секторная скорость планет постоянна.

Период τ обращения планеты – время полного прохождения траектории - находится из условия (a, b есть большая и малая полуоси эллипса соответственно)

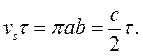
Поэтому третий закон Кеплера выражает общее свойство для всех планет Солнечной системы:

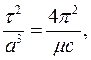(5.14)

то есть отношение квадратов периодов планет τ² к кубам их больших полуосей a³ есть постоянная величина для всех планет солнечной системы.

Доказательство.

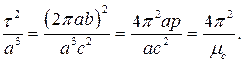
Решение задач о движении планет использует следующие соотношения между параметрами эллипса:

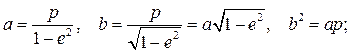(5.15)

Лекция 6.Модель «система материальных точек».

Система материальных точек есть набор конечного числа точек N, с постоянными конечными массами, взаимодействующих между собой, а также с другими телами, не включенными в систему. Мерами взаимодействий являются главный вектор 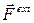внешних силсистемы и главный вектор 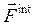внутренних сил взаимодействий системы:

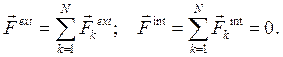(6.1)

Здесь 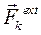есть главный вектор всех внешних сил взаимодействий точки с номером k, а 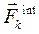есть главный вектор всех внутренних сил взаимодействий этой точки со всеми остальными точками системы.

Дифференциальные уравнения движения системы точек.

Это есть совокупность дифференциальных уравнений движения всех точек:

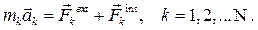(6.2)

Система (6.2), записанная в выбранном базисе, имеет 3N скалярных уравнений, в которых число скалярных неизвестных (движение, силы) больше, чем число уравнений. Система (6.2) иногда незамкнута.

Введем новые понятия для системы точек, и с их помощью опишем некоторые свойства движения и взаимодействия точек системы.

Определения.

Центр масс системы точек есть точка С, определяемая массами точек 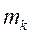и их векторами положения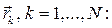

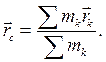(6.3)

При движении системы центр масс имеет скорость 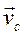и ускорение :

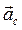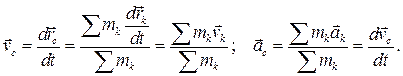(6.4)

Здесь 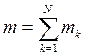называют массой системы.

Теоремы динамики системы материальных точек.

Теорема о движении центра масс:

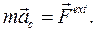(6.5)

Определения.

Импульс системы:

(6.6)

Момент импульса системы относительно неподвижной точки О (оси Oz):

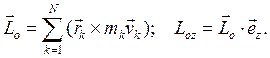(6.7)

Кинетическая энергия системы точек:

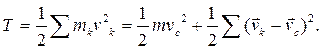(6.8)

Теорема об изменении импульса:

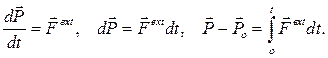(6.9)

Теорема об изменении момента импульса:

(6.10)

Здесь 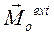есть главный момент всех внешних сил системы.

Теорема об изменении кинетической энергии:

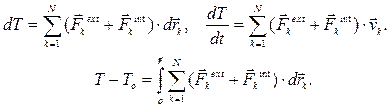(6.11)

Законы сохранения.

Закон сохранения вектора импульса системы или его проекции на ось.

Если 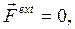то 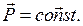(6.12)

Если то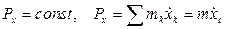

Закон сохранения вектора положения центра масс или его проекции на ось Оx :

Если 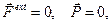, то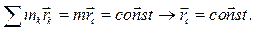

Если 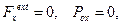, то (6.13)

Закон сохранения вектора момента импульса или его проекции на ось:

Если 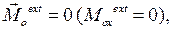то 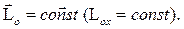(6.14)

Закон сохранения механической энергии: если все работающие силы потенциальны, то

(6.15)

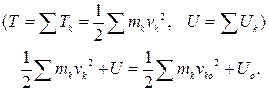
Задача 6.1. Призма 1 с массой 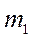может двигаться по гладкой горизонтальной поверхности. Гладкая призма 2 с массой 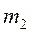скользит по гладкой боковой поверхности призмы 1 , образующей угол α с горизонтом. Найти общий класс движений системы двух призм, а также силы взаимодействий призм между собой и с горизонтальной плоскостью. Найти также величину перемещения 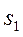призмы 1 за то время, когда призма 2 переместится вдоль боковой поверхности призмы 1 на расстояние 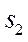. В начальный момент система призм покоилась.

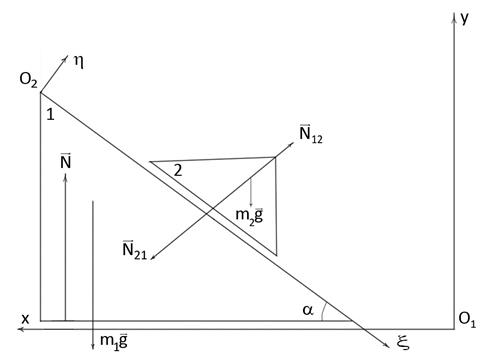
Решение 1 в декартовых координатах.

Уравнения связей и число независимых геометрических параметров, определяющих положение системы двух точек 1 и 2.

Шесть декартовых координат системы связаны четырьмя уравнениями связей:

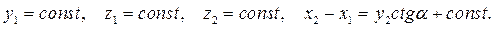(6.1.1)

Cистема двух точек имеет два независимых параметра. Пусть это будут x₁ и x₂ .

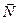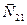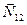
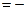
Идеальность гладких поверхностей определяет внешнюю нормальную силу реакции и внутренние действие и противодействие 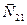внутреннего взаимодействия двух призм. Силы тяжести 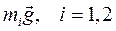есть внешние активные силы (притяжения к Земле).

Дифференциальные уравнения движения системы (6.2) в векторной форме:

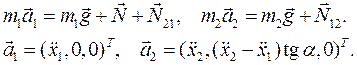
Дифференциальные уравнения движения системы в декартовых координатах Оxy, с учетом уравнения связи :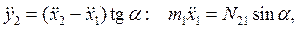

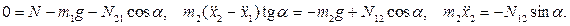(6.1.2)

Четыре уравнения имеют четыре неизвестных .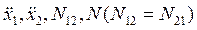

Решение этой системы имеет вид:

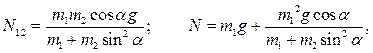
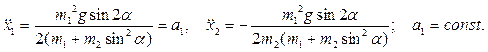
Чтобы найти связь 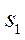и , и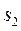спользуем закон сохранения положения центра масс системы (6.13) в проекции на ось 0x:

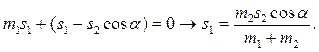
Решение 2. Применим к системе двух точек теорему о движении центра масс а затем напишем уравнение движения точки 2.

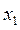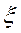Уравнения связей (6.1.1) и аксиомы сил те же, что в первом решении. Используем далее независимые параметры и , где

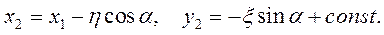
Теорема о движении центра масс системы (6.5) в проекции на оси Ox и Oy имеет вид:

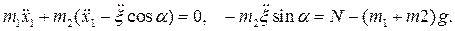
Уравнение движения призмы 2 спроектируем на неподвижные ос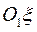и и 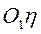, перпендикулярную и параллельную наклонной плоскости призмы 2 соответственно:

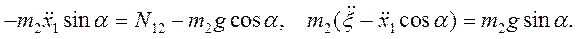
Решение четырех последних уравнений с четырьмя неизвестными дает те же результаты, однако уравнения решаются проще.

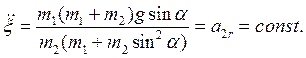
Замечание. Если требуется найти только движение системы, то достаточно двух уравнений

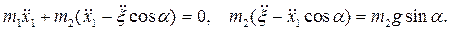
Ответ: движение системы в независимых параметрах 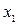и :

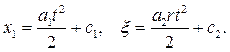
Движение системы в декартовых координатах:

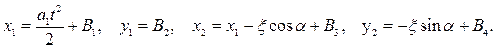
Задача двух тел.

Два твердых тела с массами m₁ и m₂ взаимодействуют между собой, причем модуль силы взаимодействия F(r) зависит от расстояния между телами r. Определить движение тел и их траектории, моделируя тела материальными точками.

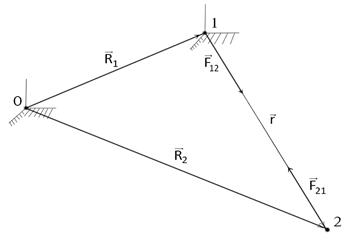
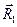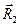Решим задачу, предполагая, что существует инерциальная система отсчета, в которой есть декартова система координат Oxyz. Пусть и определяют в этой системе положения точек 1 и 2 соответственно. Так как учитывается только взаимодействие точек между собой, то, обозначая 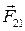силу действия точки 1 на точку 2, а силу 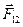противодействия точки 2 на точку 1, дифференциальные уравнения движения системы запишем в виде:

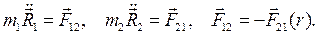
Система двух точек есть замкнутая система 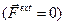и от начальных условий, покоится или движется равномерно и прямолинейно, то есть его движение известно.

Теорема. Решение задачи двух взаимодействующих точек в поле сил взаимодействия, зависящих от расстояния между ними, сводится к решению задачи движения одной точки с массой 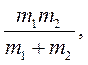в том же поле центральной силы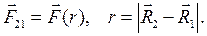

Доказательство. Умножая второе уравнение на 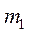, а первое уравнение - на 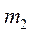,и вычитая из второго уравнения первое, получим следующее уравнение:

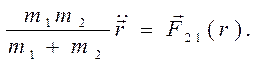(6.16)

Это уравнение имеет такой же вид, а значит и такое же по форме решение, как уравнение движения точки 2 по отношению неподвижной точке 1, (5.3) - (5.9):

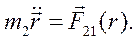
Достаточно только в решении последнего уравнения заменить массу 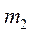на приведенную массу 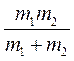. Окончательно, движение точек 1 и 2 определяется уравнениями

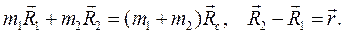
в виде:

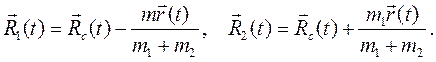
Движение двух взаимодействующих точек в гравитационном поле.

В гравитационном поле (5.10) уравнение движения точки1 по отношению к точке 2 имеет вид:

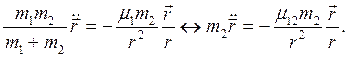(6.17)

Решение этого уравнения есть движение точки 2 относительно подвижного центра притяжения 1, постоянная Гаусса которого равна 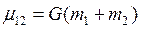(при неподвижном центре 1 она была равна 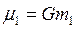) Траектории обеих точек есть конические сечения с фокусом, расположенным в точке 1. Их геометрические параметры вычисляются так же, как в задаче с заменой массы на. Заметим, что все векторы записаны в одном и том же базисе инерциальной системы координат.

Применение уравнения (6.17) к солнечной системе с заменой массы 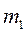на массу 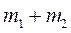приводит к уточненной формулировке законов Кеплера, с учетом движения Солнца. Они имеют ту же формулировку, как и в (5.13), (5.15), (5.17), только постоянную Гаусса в них необходимо заменить на 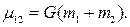где 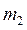есть масса планеты. Траектории планет есть эллипсы, фокусы траекторий планет совпадают с Солнцем.

Движение двух взаимодействующих точек в осях Кенига. Так как базис осей Кенига совпадает с базисом исходной инерциальной системы координат, а центр масс С движется равномерно и прямолинейно, то система координат Кенига с началом в центре масс инерциальна.

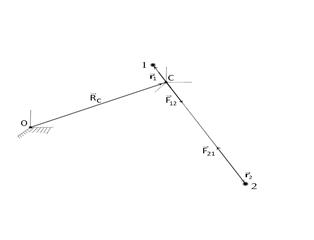
По отношению к осям Кенига уравнения движения двух точек запишутся в виде:

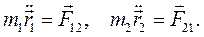(6.18)

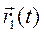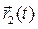Здесь и определяют движение точек 1 и 2 по отношению к системе координат Кенига, при этом

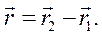
Умножая второе уравнение (6.18) на 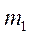, а первое - на 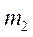и вычитая из второго уравнения первое, снова получим уравнение. После его решения движение точек в осях Кенига найдем из определения центра масс 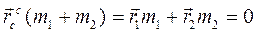по формулам:

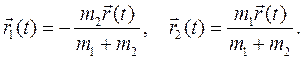
Лекция 7.Модель «абсолютно твердое тело».

Движение абсолютно твердого тела.

По определению, расстояния между любыми двумя точками твердого тела не меняются, когда тело движется.

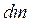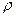Пусть в теле элементарная масса , занимает объём . Массовая плотность - масса единицы объёма, - есть .

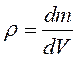Выберем в теле систему координат 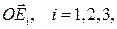для индивидуализации положения массы 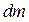в теле вектором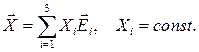

При движении твердого тела по отношению к неподвижной системе координат 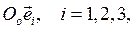вектор 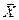вращается вместе с телом, и его запись в неподвижном базисе производится с помощью ортогональной матрицы вращения 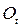, сохраняющей расстояние между точками тела и ориентацию подвижного базиса. В неподвижном базисе вектор 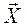обозначим :

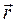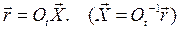(7.1)

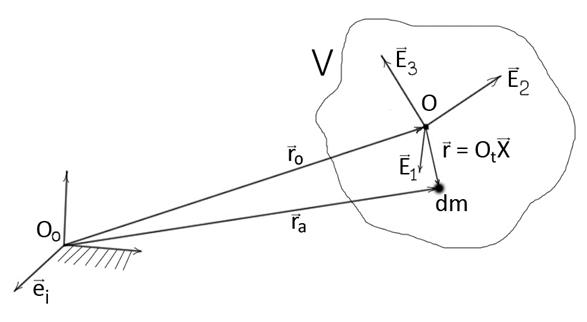
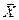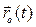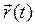Движение твердого тела есть движение всех ее точек. Для любой точки тела определим ее движение в неподвижной системе координат как сумму двух векторов: и , определяющих соответственно поступательное и вращательное движение как составляющие абсолютного движения твердого тела:

(7.2)

Здесь 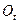есть ортогональная матрица перехода всех векторов, определенных в подвижном базисе, к неподвижному базису. Её определитель равен +1. Для таких матриц

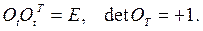(7.2)

обратная матрица 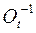равна транспонированной матрице :

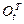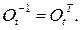
Задать движение твердого тела значит задать поступательную часть движения тремя координатами вектора полюса и тремя независимыми элементами матрицы вращения. Таким образом, произвольное движение задается 6 независимыми параметрами, то есть имеет 6 степеней свободы.

Рассмотрим различные виды движений твердого тела и их уравнения связей, уменьшающие его число степеней свободы.

Поступательное движение. Имеет 3 степени свободы из шести, так как элементы матрицы вращений постоянны, а движение задается

Сферическое движение (вращение вокруг неподвижной точки О).

Вращение тела вокруг неподвижной оси. В теле имеется две неподвижные точки. Тогда все точки оси (Оz) неподвижны. Нет поступательного движения, а вращательное движение задается одним параметром – углом поворота подвижных векторов базиса и вокруг неподвижной оси Оz .

Ниже представим ограничения (связи) для других видов движения твердого тела.

Скорости точек твердого тела. Угловая скорость тела.

Скорость любой точки тела определим в неподвижном базисе:

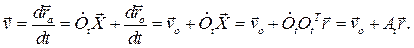(7.3)

Матрица A_t есть антисимметричная матрица, что доказывается с помощью (7.2):

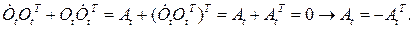
Тогда из (7.3) получим

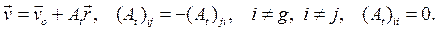(7.4)

Вектор 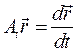можно представить следующим образом:

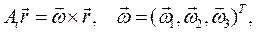
так как

где три различных элемента матрицы 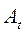, по определению, образуют вектор угловой скорости твердого тела:

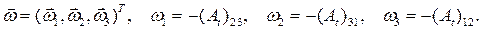
Тогда скорость точки тела вычисляется как векторная сумма скорости поступательного движения 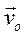с выбранным полюсом О и скорости вращательного движения 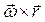по отношению к полюсу :

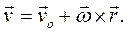(7.5)

Вектор угловой скорости 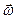не зависит от выбора полюса О и определяется только матрицей вращения .

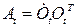Из (7.5) следует связь скоростей любых двух точек А и В тела:

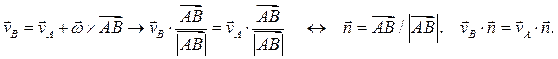
Итак: проекции скоростей любых двух точек твердого тела на направление вектора 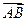, соединяющего точки, равны.

Кинематика частных движений твердого тела.

Вращение тела вокруг неподвижной оси. Существуют хотя бы две точки тела, которые имеют нулевые скорости для любого момента времени. Тогда неподвижны в теле все точки, лежащие на оси, проходящей через эти неподвижные точки.

Возьмем одну неподвижную точку за полюс О, а ось Оz проведем через другую неподвижную точку. Будем говорить, что твердое тело вращается вокруг неподвижной оси Оz.

В матрице вращения 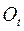и матрице 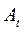есть угол 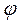вращения вокруг оси Оz подвижного базиса по отношению к неподвижному базису:

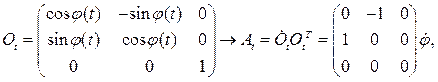
откуда вектор угловой скорости 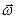имеет в неподвижном базисе одну ненулевую компоненту :

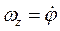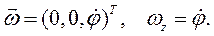(7.6)

Во вращении твердого тела вокруг неподвижной оси вектор угловой скорости параллелен оси вращения .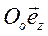

По (7.5) скорости точек тела перпендикулярны к оси вращения и к вектору 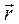. Точки тела движутся по окружностям с радиусами R и имеют величину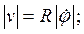

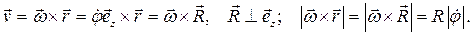
4. Плоское движение твердого тела. Скорость полюса 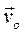расположена в неподвижной плоскости 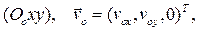а угловая скорость перпендикулярна этой плоскости 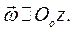Плоское движение есть композиция поступательного и вращательного движений.

Для двух точек А и В плоской фигуры скорости этих точек лежат в плоскости фигуры, а угловая скорость ей перпендикулярна.

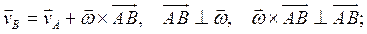(7.7)

Плоское движение имеет три степени свободы. Движение определяется уравнениями:

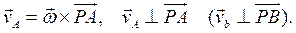
Для непоступательного плоского движения твердого тела в любом положении тела существует точка Р плоской фигуры ( или ее продолжения), скорость которой равна нулю. Эту точку Р называют мгновенный центр скоростей плоской фигуры. Взяв её за полюс, из (7.7) получим, что скорость любой точки А плоской фигуры перпендикулярна вектору РА, соединяющего точку с мгновенным центром скоростей.