Лекция 9. Динамика твердого тела. 2 страница
Проверим это:
 Аналогичные вычисления приводят к результатам:
Аналогичные вычисления приводят к результатам:
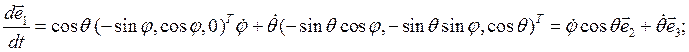
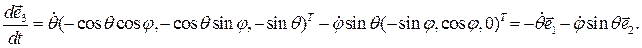
Наконец, по формуле (2.13) вектор ускорения принимает следующий вид:
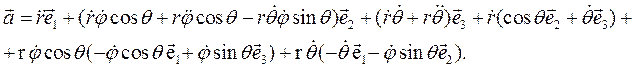
Таким образом, компоненты вектора ускорения в ортонормированном базисе сферических координат 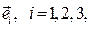 запишутся в следующем виде:
запишутся в следующем виде:
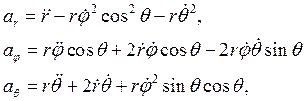 (3.14)
(3.14)
Лекция 4.Центральные силы. Потенциальные силы, потенциальная энергия. Силы, имеющие осевую симметрию. Идеальные силы.
В лекции 1 была показана связь движения точки с силами ее взаимодействия с другими телами. Именно характер сил влияет на возможность интегрирования дифференциальных уравнений движения точки и записи результатов интегрирования уравнений движения в виде теорем динамики точки в интегральной форме и законов сохранения. Рассмотрим ниже подробнее этот вопрос.
Определение. Сила, вызывающая движение точки, называется центральной, если в любом положении точки линия действия силы проходит через неподвижную точку О (центр, полюс). По определению, вектор положения 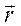 точки параллелен вектору силы
точки параллелен вектору силы 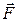 .
.
Определение. Элементарной работой силы 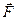 на элементарном перемещении
на элементарном перемещении 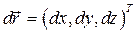 называется скаляр dА, равный скалярному произведению вектора силы и вектора элементарного перемещения
называется скаляр dА, равный скалярному произведению вектора силы и вектора элементарного перемещения  :
:

Определение. Сила называется идеальной, если в любом положении точки, совместимом со связями, и на любом элементарном перемещении, допустимом связями, элементарная работа силы равна нулю.
Определение. Сила 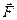 называется потенциальной силой, если её элементарная работа есть со знаком минус полный дифференциал некоторой скалярной функции U , зависящей от скалярных параметров, определяющих положение точки:
называется потенциальной силой, если её элементарная работа есть со знаком минус полный дифференциал некоторой скалярной функции U , зависящей от скалярных параметров, определяющих положение точки:
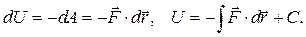 (4.1)
(4.1)
Функция U для данной силы называется ее потенциальной энергией.
По определению (4.1), если сила 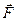 есть векторная сумма потенциальных сил, то точка имеет потенциальную энергию, равную сумме потенциальных энергий всех сил.
есть векторная сумма потенциальных сил, то точка имеет потенциальную энергию, равную сумме потенциальных энергий всех сил.
Определение. Если в евклидовом пространстве R3 для каждого положения материальной точки задана потенциальная сила, зависящая от параметров, задающих ее положение (от координат), то говорят, что в пространстве задано силовое поле.
Вычисление потенциальных энергий потенциальных сил .
Сила тяжести 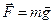 . В декартовых осях Oxyz , где ось Oy направлена по вертикали,
. В декартовых осях Oxyz , где ось Oy направлена по вертикали,
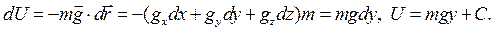
Если принять, что U(O) = 0, то С = 0 , и
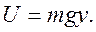 (4.2)
(4.2)
Сила гравитационного притяжения 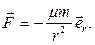 Центральная сила записана в базисе сферических координат. Тогда
Центральная сила записана в базисе сферических координат. Тогда
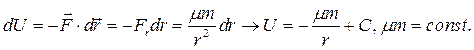
Принимаем, что U(∞)=0. Тогда С = 0 и
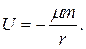 (4.3)
(4.3)
Сила упругой пружины 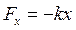 , где
, где 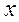 есть удлинение (сжатие) пружины. Коэффициент
есть удлинение (сжатие) пружины. Коэффициент 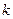 - жесткость пружины. Сила зависит только от удлинения (сжатия) пружины, поэтому
- жесткость пружины. Сила зависит только от удлинения (сжатия) пружины, поэтому
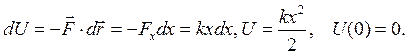 (4.4)
(4.4)
Здесь dx есть элементарное удлинение пружины при растяжении.
Теоремы динамики точки. Законы сохранения.
Интегрирование дифференциальных уравнений движения представляет в общем случае существенные трудности. Однако, для некоторых типов взаимодействий (типов сил) результаты интегрирования дифференциальных уравнений движения могут быть легко предсказаны и сформулированы с помощью введения нескольких новых понятий. Докажем это.
Определения.
Импульс (количество движения) материальной точки есть вектор
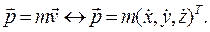 (4.5)
(4.5)
Момент импульса (момент количества движения)точки относительно неподвижной точки О есть вектор
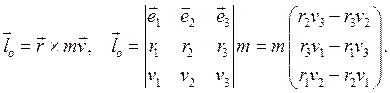 (4.6)
(4.6)
3. Моментом импульса относительно оси  называется скаляр - проекция на эту ось вектора
называется скаляр - проекция на эту ось вектора 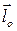 :
:
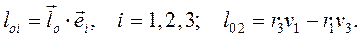 (4.7)
(4.7)
Кинетическая энергия точки есть скаляр
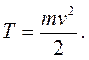 (4.8)
(4.8)
Момент силы 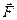 относительно точки О есть вектор
относительно точки О есть вектор
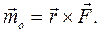 (4.9)
(4.9)
6. Проекция вектора 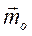 на ось Оz называется моментом силы относительно оси Oz:
на ось Оz называется моментом силы относительно оси Oz:
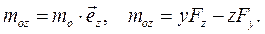 (4.10)
(4.10)
7. Работа силы 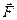 на пути из положения
на пути из положения 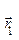 в положение
в положение 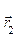 есть скаляр
есть скаляр
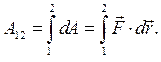 (4.11)
(4.11)
Здесь 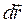 - элементарное перемещение в некотором положении
- элементарное перемещение в некотором положении 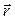 точки на пути.
точки на пути.
Если сила 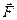 потенциальная сила, то работа силы на пути не зависит от формы пути и вычисляется как разность потенциальных энергий U точки в начале и в конце пути:
потенциальная сила, то работа силы на пути не зависит от формы пути и вычисляется как разность потенциальных энергий U точки в начале и в конце пути:
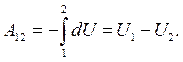 (4.12)
(4.12)
Теорема об изменении импульса точки .
Из второго закона Ньютона 
следует дифференциальная форма теоремы об изменении импульса
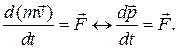 (4.13)
(4.13)
Если главный вектор сил 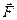 зависит либо от времени, либо от скорости, то (4.13) можно проинтегрировать на интервале времени [
зависит либо от времени, либо от скорости, то (4.13) можно проинтегрировать на интервале времени [ 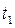 ,
, 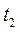 ]
]
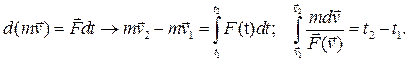 (4.14)
(4.14)
Уравнения (4.14) есть интегральные формы теоремы об изменении импульса.
Закон сохранения импульса точки.
Если в (4.13) главный вектор всех сил 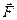 = 0 , то имеет место закон сохранения импульса
= 0 , то имеет место закон сохранения импульса
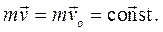 (4.15)
(4.15)
Если в (4.13) равна нулю компонента силы по оси Оx, то сохраняется импульс точки в проекции на эту ось:
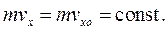 (4.16)
(4.16)
Теорема об изменении момента импульса (момента количества движения) точки.
Используем определения (4.6) и (4.9). Тогда дифференциальная форма теоремы имеет вид:
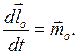
Действительно,
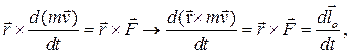 (4.17)
(4.17)
что и требовалось доказать.
Здесь 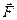 - главный вектор (сумма всех сил), а
- главный вектор (сумма всех сил), а 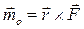 - главный момент (сумма моментов) всех сил.
- главный момент (сумма моментов) всех сил.
Закон сохранения момента импульса точки.
1. Если главный момент всех сил 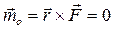 равен нулю относительно точки О, то из (4.17) следует закон сохранения момента импульса относительно этой точки:
равен нулю относительно точки О, то из (4.17) следует закон сохранения момента импульса относительно этой точки:
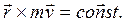 (4.18)
(4.18)
Определение. Говорят, что система сил имеет осевую симметрию, если в любом положении движущейся точки линии действия сил расположены в плоскости, проходящей через эту точку и некоторую неподвижную ось (0z).
Задача. Доказать, что главный момент системы сил, имеющих осевую симметрию относительно оси 0z, равен нулю относительно этой оси.
2. Если равна нулю проекция главного момента сил 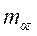 на ось Оz , то из (4.17) следует закон сохранения момента импульса
на ось Оz , то из (4.17) следует закон сохранения момента импульса 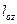 относительно оси 0z:
относительно оси 0z:
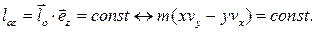 (4.19)
(4.19)
Таким образом, закон сохранения момента импульса относительно оси имеет место тогда, когда система сил имеет относительно этой оси осевую симметрию.
Теорема об изменении кинетической энергии точки.
Все формы теоремы используются тогда, в качестве переменных выбирается скорость точки и какие – либо её положения. Все формы теоремы есть формы записи закона Ньютона или способ его интегрирования в переменных скорость – положение.
Дифференциальные формы теоремы об изменении кинетической энергии 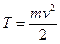 .
.
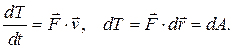 (4.20)
(4.20)
Интегральная форма теоремы об изменении кинетической энергии.
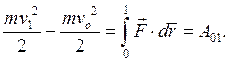 (4.21)
(4.21)
Задача. Доказательство теорем (4.20) и (4.21) провести самостоятельно.
Закон сохранения механической энергии.
Если все работающие силы потенциальны, результатом интегрирования будет закон сохранения механической энергии E = T + U .
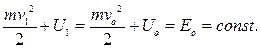
 (4.22)
(4.22)
Задача 4.1. Кольцо массой m скользит по неподвижной гладкой проволоке, имеющей форму параболы 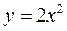 , в вертикальной плоскости, в поле постоянной силы притяжения к Земле. Определить силу реакции проволоки
, в вертикальной плоскости, в поле постоянной силы притяжения к Земле. Определить силу реакции проволоки 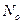 в нижнем положении кольца, если в его начальном положении
в нижнем положении кольца, если в его начальном положении 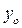 кольцо имело скорость
кольцо имело скорость 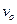 .
.
Решение. Покажем, как выглядит решение, если представить движение в декартовых координатах, а затем в естественной форме.
В обоих случаях решение можно получить с помощью дифференциальных уравнений движения (1.4) или (3.9), добавив к ним уравнения связей.
Однако вначале проанализируем тип сил, вызывающих движение точки. Сила тяжести есть потенциальная сила, имеющая потенциальную энергию 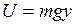 (ось 0y направлена вертикально вверх), а сила реакции гладкой проволоки есть идеальная сила – она не работает при движении точки, так как ее элементарная работа равна нулю в любом положении точки на траектории:
(ось 0y направлена вертикально вверх), а сила реакции гладкой проволоки есть идеальная сила – она не работает при движении точки, так как ее элементарная работа равна нулю в любом положении точки на траектории: 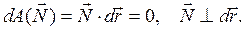
В таком случае имеет место закон сохранения механической энергии (4.22), из которого можно найти скорость точки в любом положении по известным начальным значениям положения и скорости точки. Именно знание скорости точки, как следует из уравнений движения, достаточно для нахождения силы реакции в любом ее положении.
Еще раз подчеркнем, что закон сохранения механической энергии есть результат интегрирования уравнений ее движения.
Решение задачи в декартовых координатах .
1. Уравнения связей:
 (4.1.1)
(4.1.1)
Уравнения движения точки в нижнем положении с учетом уравнений связей (4.1.1) в этом положении (x = 0) имеют вид:
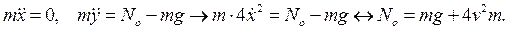
Закон сохранения механической энергии:
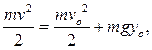 (4.1.2)
(4.1.2)
откуда скорость в нижнем положении равна:
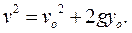
Ответ: 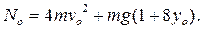
Решение задачи с помощью естественных уравнений движения:
Проекция закона Ньютона на нормаль:
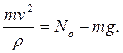 (4.1.3)
(4.1.3)
Вычисление радиуса кривизны 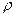 параболы по формуле:
параболы по формуле:
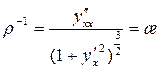
дает значение: 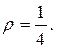
С учетом скорости 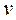 из (4.1.2) и найденного значения
из (4.1.2) и найденного значения 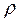 , из (4.1.3) получаем для силы реакции
, из (4.1.3) получаем для силы реакции 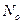 тот же ответ.
тот же ответ.
Любую задачу динамики точки можно решить, используя декартовы координаты, однако в некоторых задачах проще применять криволинейные координаты.
Задача 4.2. Материальная точка М движется по гладкой внешней поверхности неподвижного прямого кругового конуса с вертикальной осью 0z и углом 2 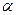 его раствора. Найти силу реакции конуса N для любого положения точки, если в начальном положении точка получила горизонтальную скорость
его раствора. Найти силу реакции конуса N для любого положения точки, если в начальном положении точка получила горизонтальную скорость  на расстоянии
на расстоянии 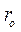 от вершины конуса 0.
от вершины конуса 0.
Решение:решим задачу в сферических координатах.
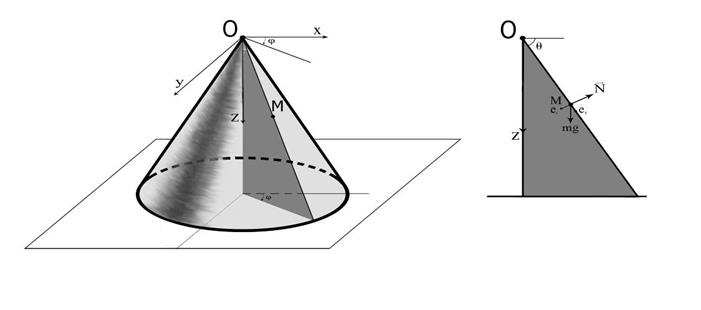
Условие нахождения точки на конусе запишем в виде уравнений связей:
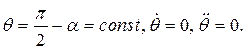
Выберем за независимые координаты 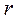 и
и 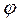 . Интегрируя уравнение закона Ньютона в проекции на базисный вектор
. Интегрируя уравнение закона Ньютона в проекции на базисный вектор 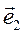 , получим:
, получим:
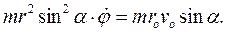
Силу реакции конуса N найдем из уравнения закона Ньютона в проекции на базисный вектор 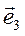 :
: 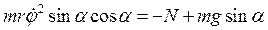 , откуда
, откуда
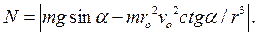
Решим задачу 4.2 в цилиндрических координатах.
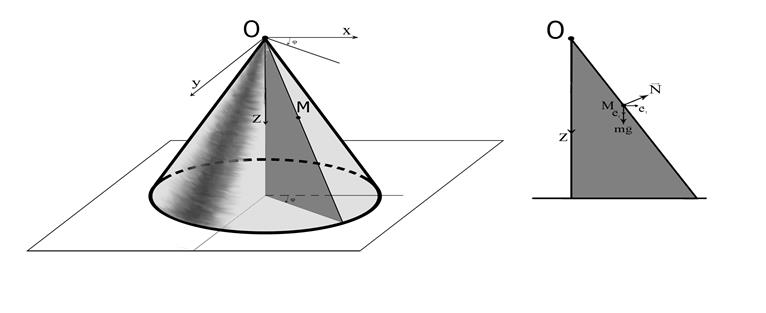
Уравнения связи (условие нахождения точки на конусе):
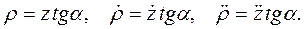
Так как для сил имеет место осевая симметрия относительно оси 0z,то имеетместо закон сохранения момента импульса относительно оси 0z:
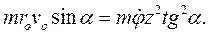
Закон Ньютона в проекциях на направления базисных векторов  и
и 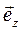 с использованием (2.14) запишется так:
с использованием (2.14) запишется так:

Исключив 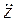 из двух уравнений, получаем:
из двух уравнений, получаем:
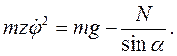
Наконец, с помощью найденной из закона сохранения момента импульса относительно оси 0z величины 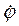 , находим силу реакции:
, находим силу реакции:
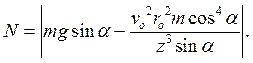
Лекция 5. Движение материальной точки в центральном поле сил.
Если материальная точка движется под действием силы притяжения или отталкивания от неподвижного центра 0 (центральная сила), то она сохраняет момент импульса относительно 0:
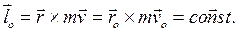 (5.1)
(5.1)
Тогда точка может двигаться только в плоскости, проходящей через 0 и перпендикулярной векторам начального состояния 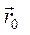 и
и 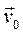 . В таком случае для описания ее движения достаточно ввести полярные координаты
. В таком случае для описания ее движения достаточно ввести полярные координаты 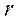 и
и 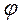 .
.
Запишем (5.1) в виде:
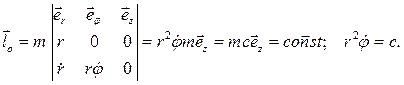 (5.2)
(5.2)
Пусть центральная сила зависит от расcтояния r (полярная координата) между полюсом 0 и текущим положением точки, то есть проекция силы 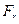 на
на 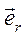 есть
есть
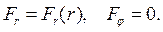 (5.3)
(5.3)
Тогда сила образует поле с потенциальной энергией U(r):
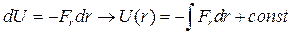 (5.4)
(5.4)
и выполняется закон сохранения механической энергии
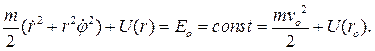 (5.5)
(5.5)
С использованием законов сохранения (5.2) и (5.5) для нахождения движения точки
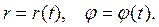 (5.6)
(5.6)
запишем (5.5) в виде:
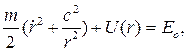
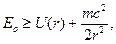
Сначала решаем задачу нахождения 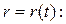
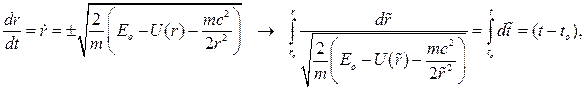
Интегрирование проведено при возрастании r. Затем ищем φ = φ(t):

Траекторию точки найдем из формулы:
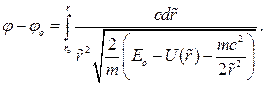 (5.7)
(5.7)
Траектории точки в гравитационном (ньютоновском) поле сил.
Гравитационное поле есть центральное поле с силой притяжения 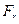 и потенциальной энергией
и потенциальной энергией 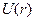 :
:
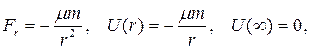
где m есть масса точки, 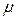 есть постоянная Гаусса (Gauss) неподвижного притягивающего центра. Интегрирование (5.7) при условии, что
есть постоянная Гаусса (Gauss) неподвижного притягивающего центра. Интегрирование (5.7) при условии, что 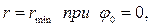 получим траекторию в виде:
получим траекторию в виде:
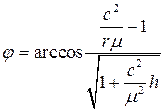
или
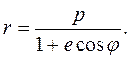 (5.8)
(5.8)
Это есть уравнение конических сечений с параметром p и эксцентриситетом e , определенные по формулам:
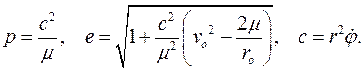
Формулы Бинэ.
Дифференциальное уравнение движения точки в полярных координатах в проекции на базисный вектор 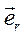
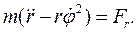
с помощью (5.2) можно записать в форме, предложенной Бинэ:
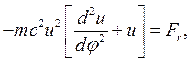 (5.9)
(5.9)
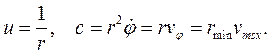
Для доказательства (5.9) достаточно использовать следующие соотношения:
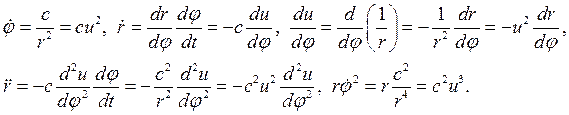
Если (5.9) принято называть второй формулой Бинэ, то первой формулой Бинэ называют выражение квадрата скорости точки в виде:
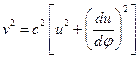 .
.
Покажем, что уравнение (5.9) удобно для нахождения траектории точки в центральном поле сил на примере нахождения траектории в гравитационном поле сил 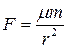 с потенциальной энергией
с потенциальной энергией 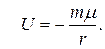
Уравнение (5.9) примет вид:
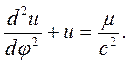 (5.10)
(5.10)
Это линейное неоднородное уравнение второго порядка. Его решение есть сумма частного решения 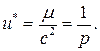 и общего решения однородного уравнения
и общего решения однородного уравнения
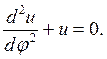
Тогда общее решение можно представить в виде:
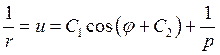
Множество его решений для различных значений параметров 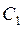 и
и 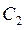 есть различные траектории точки.
есть различные траектории точки.
Примем, что 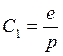 больше нуля,
больше нуля, 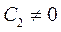 . Тогда решение примет вид:
. Тогда решение примет вид:
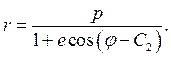
Это уравнение конического сечения. Здесь p есть параметр конического сечения, e есть эксцентриситет.
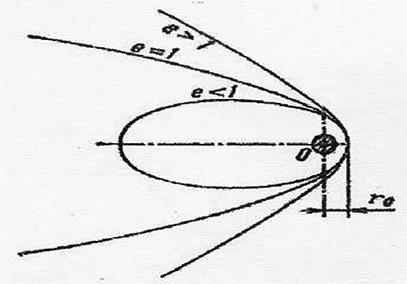
Далее. Как и раньше, примем, что угол φ = 0, когда расстояние от точки до притягивающего центра минимально и равно rmin = r0 . Тогда уравнение конического сечения запишется 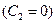 так же как и (5.8):
так же как и (5.8):
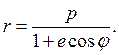
Если e < 1 , то кривая есть эллипс. При e = 0 кривая есть окружность. Если e = 1 , то кривая есть парабола, а если e > 1 , то кривая есть гипербола.
Можно показать, что постоянное значение эксцентриситета и вид траектории определяется начальным состоянием точки - r0 и v0 в любом месте на траектории.
Оценим эту зависимость при φ = 0 , когда величина расстояния 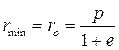 до притягивающего центра 0 минимальна, радиальная скорость
до притягивающего центра 0 минимальна, радиальная скорость 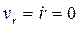 . Тогда полная скорость v =
. Тогда полная скорость v = 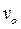 . Из закона сохранения момента импульса (5.2) следует:
. Из закона сохранения момента импульса (5.2) следует:
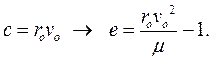 (5.11)
(5.11)
Отсюда:
при 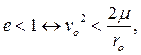 траектория есть эллипс, (5.12)
траектория есть эллипс, (5.12)
при 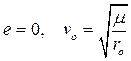 траектория есть окружность, (5.13)
траектория есть окружность, (5.13)
при 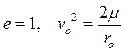 траектория есть парабола, (5.14)
траектория есть парабола, (5.14)
и, наконец, при 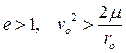 траектория есть гипербола. (5.15)
траектория есть гипербола. (5.15)
Задача 5.1. Тело, моделируемое материальной точкой, запускается на высоте H над Землей радиуса R со скоростью 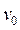 , перпендикулярной местной вертикали. Какова должна быть величина скорости запуска тела, чтобы оно бесконечно удалилось от Земли? Сила гравитационного притяжения точки к Земле у поверхности Земли равна
, перпендикулярной местной вертикали. Какова должна быть величина скорости запуска тела, чтобы оно бесконечно удалилось от Земли? Сила гравитационного притяжения точки к Земле у поверхности Земли равна 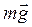 . Чему равны первая и вторая космические скорости точки на Земле
. Чему равны первая и вторая космические скорости точки на Земле 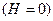 ?
?
Решение. Гравитационная сила, определяемая формулой (5.9), из условия, что на земле она равна силе тяжести, дает значение постоянной Гаусса, равное 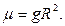 Поэтому, из формул (5.14) и (5.15) имеем следующее значение искомой скорости:
Поэтому, из формул (5.14) и (5.15) имеем следующее значение искомой скорости:
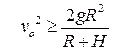 .
.
Дата добавления: 2019-07-26; просмотров: 427;
