Теплопроводность плоской стенки

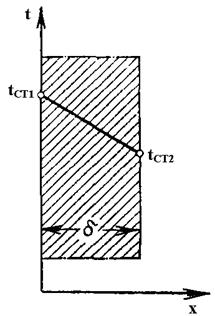
Рассмотрим передачу тепла теплопроводностью через плоскую стенку, длина и ширина которой безгранично велики по сравнению с ее толщиной, ось х расположена по нормали к поверхности стенки.

Температура наружной поверхности стенки t_ст1 и t_ст2 , причем t_ст1 > t_ст2

Примем, что температура изменяется только в

направлении оси х, т.е. температурное поле

одномерное 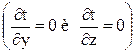. Тогда на основании

уравнения теплопроводности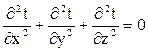

получим 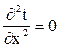(1)

Интегрирование этого уравнения приводит к функции

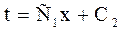(2)

где С₁ и С₂ – константы интегрирования.

Это уравнение показывает, что по толщине плоской стенки температура изменяется прямолинейно. Константы интегрирования определяются из следующих граничных условий:

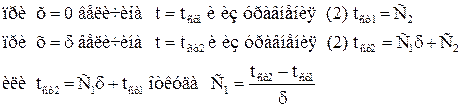
Подставив значение констант в уравнение (2) находим

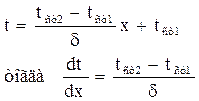
Подставив полученное выражение температурного градиента в уравнение теплопроводности, получим количество переданного тепла:

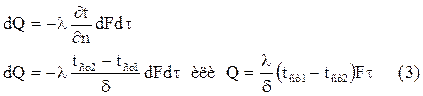
где λ – коэффициент теплопроводности материала стенки, Вт/(м·град);

δ – толщина стенки, м;

t_ст1 – t_ст2 – разность температур поверхностей стенки, град;

F – поверхность стенки, м²;

τ – время, сек.

Для непрерывного процесса передачи тепла теплопроводностью т.е.

τ = 0 получим уравнение:

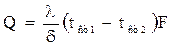(4)

Уравнение (3) и (4) являются уравнениями теплопроводности плоской стенки при установившемся процессе теплообмена.

Если плоская стенка состоит из n – слоев, тогда получим уравнение:

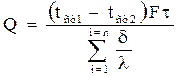
где i – порядковый номер слоя стенки;

n – число слоев.