Итеративные коды: определение, принцип построения, основные характеристики
Итеративные помехоустойчивые коды относятся к классу кодов произведения. Кодом произведения двух исходных (базовых) помехоустойчивых кодов n1и n2называется такой многомерный помехоустойчивый код N=n1*n2, кодовыми последовательностями которого являются все двумерные таблицы со строками кода n1и столбцами кода п2.
Исходные помехоустойчивые коды могут быть блоковыми и ЦК Þ блоковый итеративный код и циклический итеративный код.
Итеративные коды, также как и матричные коды, могут быть представлены в виде квадратных (п1=n2) и прямоугольных (n1≠n2) матриц или таблиц, при этом информационные символы записываемые по строкам и столбцам, могут кодироваться либо одним типом помехоустойчивого кода, либо разными.
Обобщенная структурная схема формирования двумерного итеративного кода с параметрами исходных помехоустойчивых кодов (n1,k1,d01) и (n2,k2,d02) соответственно имеет следующее построение (рис.4.1).
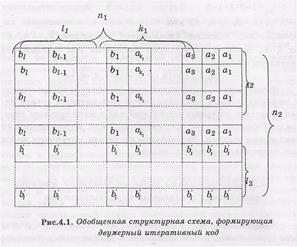
Итеративные коды могут строиться на основе использования двух, трехмерных матриц (таблиц) и более высоких размерностей. Установим основные соотношения между параметрами (характеристиками) двумерного итеративного кода, когда используются исходные помехоустойчивые коды (n1,k1,d01) и (n2,k2,d02); в общем случае данные исходные коды могут иметь как одинаковые параметры, так и разные, т.е. 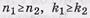 и
и 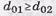 или наоборот.
или наоборот.
Из способа формирования двумерного итеративного кода (рис.4.1) следует:
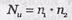 – общее количество двоичных символов в кодовой последовательности итеративного кода;
– общее количество двоичных символов в кодовой последовательности итеративного кода;
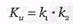 – общее количество информационных символов в кодовой последовательности Nu итеративного кода;
– общее количество информационных символов в кодовой последовательности Nu итеративного кода;
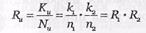 — скорость передачи кода. Так как производится умножение двух чисел, меньших единицы, то результат их произведения по величине будет меньше наименьшего из сомножителей. Это означает, что данный итеративный код будет иметь большую избыточность, чем любой из исходных кодов. Следовательно, относительная избыточность кода будет определяться равенством
— скорость передачи кода. Так как производится умножение двух чисел, меньших единицы, то результат их произведения по величине будет меньше наименьшего из сомножителей. Это означает, что данный итеративный код будет иметь большую избыточность, чем любой из исходных кодов. Следовательно, относительная избыточность кода будет определяться равенством

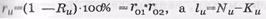 – абсолютная избыточность кода;
– абсолютная избыточность кода; 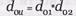 – минимальное кодовое расстояние двумерного итеративного кода. Следовательно, данный код обеспечивает коррекцию ошибок
– минимальное кодовое расстояние двумерного итеративного кода. Следовательно, данный код обеспечивает коррекцию ошибок
Если исходные помехоустойчивые коды 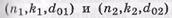 корректируют соответственно t1 и t2 ошибочных символов, то двумерный итеративный код обеспечивает исправление
корректируют соответственно t1 и t2 ошибочных символов, то двумерный итеративный код обеспечивает исправление
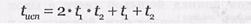
двоичных символов или коррекцию пакетов ошибок кратностью
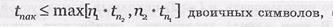
где tn1 и tn2 -кратности пакетов ошибок, корректируемые соответственно исходными кодами (n1,k1,d01) и (n2,k2,d02)
Необходимо отметить, что для всех групповых кодов, корректирующих 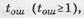 необходимо чтобы выполнялось следующее неравенство
необходимо чтобы выполнялось следующее неравенство

Коррекция пакетных ошибок возможна только при реализации записи кодовых последовательностей одного из кодов по строкам, а считывание кодовых последовательностей второго кода по столбцам или наоборот. Коррекция пакетных ошибок обеспечивается в этом случае за счет перемежения кодовых символов. Таким образом, можно отметить, что код произведение является обобщением кода-перемежения.
Вероятность ошибочного декодирования информации при использовании двумерного итеративного кода приближенно рассчитывается как

где Рош.дек.1 и Рош.дек.2 – вероятности ошибочного декодирования исходных помехоустойчивых кодов соответственно (n1,k1,d01) и (n2,k2,d02).
Пример: код (n,k)=(24,16)
Таблица кодирования для k=16 имеет вид:
| а1 | а2 | а3 | а4 | b1 |
| а5 | а6 | а7 | а8 | b2 |
| а9 | а10 | а11 | а12 | b3 |
| а13 | а14 | а15 | а16 | b4 |
| b5 | b6 | b7 | b8 |
а1-а16 – информационные символы
b1-b8 – проверочные символы
При (а1-а16)=(1110 1001 1000 0010), (b1-b8)=(1011 1101) таблица кодирования выглядит следующим образом:
Достоинствами итеративных кодов являются:
1. высокая корректирующая способность (даже при вероятности ошибок в канале связи Рk=0,5),
2. выбором соответствующего количества исходных помехоустойчивых кодов и их параметров можно обеспечить малую вероятность ошибочного приема информации, т.е минимальную вероятность ошибок декодера Рош.дек.;
3. минимальная сложность аппаратной и программной реализации;
4. возможность защиты информации от несанкционированного доступа и др.
Недостатками данных кодов являются:
1. большая избыточность кодов;
2. большая задержка информации при декодировании;
3. высокая сложность реализации систем цикловой синхронизации распределителей информации кодека и др.
В связи с этим в системах связи широкое применение получили каскадные коды, которые являются дальнейшим развитием итеративных кодов.
Дата добавления: 2019-04-03; просмотров: 888;
