Примерами префиксных кодов являются коды Шеннона-Фано и Хаффмана.
Код Шеннона-Фано
Сообщения алфавита источника выписывают в порядке убывания вероятностей их появления. Далее разделяют их на две части так, чтобы суммарные вероятности сообщений в каждой из этих частей были по возможности почти одинаковыми. Припишем сообщениям первой части в качестве первого символа – 0, а второй – 1 (можно наоборот). Затем каждая из этих частей (если она содержит более одного сообщения) делится на две по возможности равновероятные части, и в качестве второго символа для первой из них берется 0, а для второй – 1. Этот процесс повторяется, пока в каждой из полученных частей не останется по одному сообщению.
Пример:
Р(а1)=0,1 Р(а2)=0,15 Р(а3)=0,15 Р(а4)=0,1 Р(а5)=0,05
Р(а6)=0,05 Р(а7)=0,2 Р(а8)=0,07 Р(а9)=0,09 Р(а10)=0,04
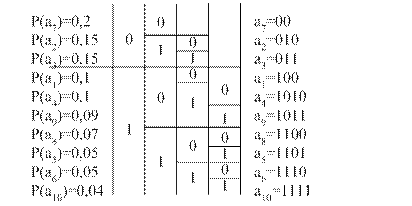

Рис. Кодовое дерево кода Шеннона – Фано
Методика Шеннона – Фано не всегда приводит к однозначному построению кода, поскольку при разбиении на части можно сделать больше по вероятности как верхнюю, так и нижнюю части. Кроме того, методика не обеспечивает отыскания оптимального множества кодовых слов для кодирования данного множества сообщений. (Под оптимальностью подразумевается то, что никакое другое однозначно декодируемое множество кодовых слов не имеет меньшую среднюю длину кодового слова, чем заданное множество.) Предложенная Хаффманом конструктивная методика свободна от отмеченных недостатков.
Код Хаффмана
Буквы алфавита сообщений выписывают в основной столбец таблицы кодирования в порядке убывания вероятностей. Две последние буквы объединяют в одну вспомогательную букву, которой приписывают суммарную вероятность. Вероятность букв, не участвовавших в объединении, и полученная суммарная вероятность слова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние объединяют. Процесс продолжается до тех пор, пока не получим единственную вспомогательную букву с вероятностью, равной единице.
Для нахождения кодовой комбинации необходимо проследить путь перехода знака по строкам и столбцам таблицы. Это наиболее наглядно осуществимо по кодовому дереву. Из точки, соответствующей вероятности 1, направляются две ветви, причем ветви с большей вероятностью присваиваем символ 1, а с меньшей – 0. Такое последовательное ветвление продолжается до тех пор, пока не дойдем до вероятности каждой буквы. Двигаясь по кодовому дереву сверху вниз, можно записать для каждого сообщения соответствующие ему кодовые комбинации.
Пример:
Р(а1)=0,1 Р(а2)=0,15 Р(а3)=0,15 Р(а4)=0,1 Р(а5)=0,05
Р(а6)=0,05 Р(а7)=0,2 Р(а8)=0,07 Р(а9)=0,09 Р(а10)=0,04

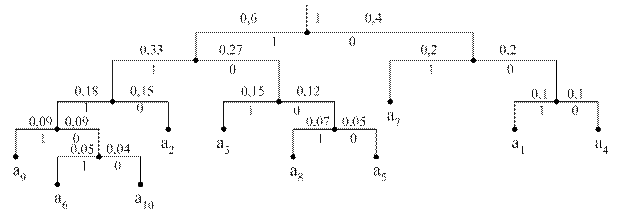
а1=001 а2=110 а3=101 а4=000 а5=1000 а6=11101 а7=01 а8=1001 а9=1111 а10=11100
Рис. Кодовое дерево кода Хаффмана
Дата добавления: 2019-04-03; просмотров: 1430;
