Первичные коды и эффективное кодирование

Первичные коды – специальный класс кодов, которые учитывают исключение избыточности информации из передаваемых сообщений с целью увеличения скорости передачи информации.

Статистическое кодирование информации (кодирование источника со­общений или сжатие информации) связано с преобразованием выходной ин­формации дискретного источника в последовательность букв заданного ко­дового алфавита. Естественно, что правила кодирования следует выбирать таким образом, чтобы с высокой вероятностью последовательность на выходе источника могла быть восстановлена по закодированной последовательности, а также, чтобы число букв кода, требуемых на одну бу­кву источника, было по возможности меньшим. В теории информации пока­зывается, что минимальное число двоичных букв кода на одну букву источ­ника, требуемых для представления выхода источника, задается энтропией источника.

Энтропия Н(А) источника сообщений А определяется как математиче­ское ожидание количества информации:

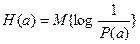, (1)

где Р(а) – вероятность того, что источник превышает сообщение “а” из ан­самбля А. Здесь математическое ожидание обозначает усреднение по всему ансамблю сообщений. При этом должны учитываться все вероятностные свя­зи между различными сообщениями.

Чем больше энтропия источника, тем больше степень неожиданности передаваемых им сообщений в среднем, т.е. тем более неопределенным явля­ется ожидаемое сообщение. Поэтому энтропию часто называют мерой неоп­ределенности сообщения. Можно характеризовать энтропию так же, как меру разнообразия выдаваемых источником сообщений. Если ансамбль содержит К различных сообщений, то Н(а)≤logK, причем равенство имеет место толь­ко тогда, когда все сообщения передаются равновероятно и независимо. Чис­ло К называется объемом алфавита источника.

Для двоичного источника, когда К=2, энтропия максимальна при Р(а₁)=Р(а₂) 0,5 и равна 1оg 2=1 бит. Энтропия источника зависимых сообщений всегда меньше энтропии источника независимых сообщений при том же объ­еме алфавита и тех же безусловных вероятностях сообщений. Для источника с объемом алфавита К=32, когда буквы выбираются равновероятно и неза­висимо друг от друга, энтропия источника Н(А)=logК=5бит. Таким источ­ником, например, является пишущая машинка русского алфавита при хаотическом порядке нажатии клавиш. Если же буквы передаются не хаотически, а составляют связный русский текст, то они оказываются неравновероятными (буква А передается чаще, чем буква Ф, и т.п.) и зависимыми (после гласных не может появиться знак "ь"; мала вероятность сочетания более трех гласных подряд и т.п.). Анализ ансамблей текстов рус­ской художественной прозы показывает, что в этом случае энтропия менее 1,5 бит на букву. Еще меньше, около 1 бит на букву, энтропия ансамбля поэтических произведений, так как в них имеются дополнительные вероятност­ные связи, обусловленные ритмом и рифмами. Если же рассматривать в качестве источника сообщений поток телеграмм, то его энтропия обычно не пре­вышает 0,8 бит на букву, поскольку тексты довольно однообразны.

Избыточность источника æ 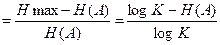(2)

показывает, какая доля макси­мально возможной при этом алфавите энтропии не используется источником.

Среднее число кодовых символов на одну букву источника (средняя длина сообщения):

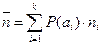, где (4)

P(a_i) – вероятность сообщения a_i,

n_i – количество двоичных символов в сообщении.

Коэффициент сжатия для первичного кода ,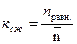

где n_равн.= log₂К – количество двоичных символов в кодовом слове при равномерном кодировании сообщений (К – количество сообщений).

Префиксные коды

Однозначность декодирования можно обеспечить, не вводя разделительного символа, если строить код так, чтобы он удовлетворял условию, известному под названием "свойство префикса". Оно заключается в том, что ни одна комбинация более кратного кода не должна совпадать с началом ("префиксом") другого кодового слова. Коды, удовлетворяющие этому условию, называют префиксными кодами. Эти коды обеспечивают однозначное декодирование принятых кодовых слов без введения дополнительной информации для их разделения, т. е. всякая последовательность кодовых символов должна быть единственным образом разделена на кодовые слова. Коды, в которых это требование выполнимо, называются однозначно декодируемыми, или кодами без запятой.

Если код префиксный, то, читая принятую последовательность подряд с начала до конца, можно установить, где кончается одно кодовое слово и начинается следующее. Например, если код префиксный и в последовательности встретился код 110, то, очевидно, в коде не должно содержаться слов (1), (11). Закодировано префиксным кодом с а₁ = (00), а₂ = (01), а₃ = (101), а₄ = (100). На рис. 1 представлен граф (кодовое дерево) префиксного кода с сообщением а₁ = (0), а₂ = (1), а₃ = (11), а₄ = (111). Из рис. 1 следует, что если свойство префикса не выполняется, то некоторые промежуточные вершины дерева могут соответствовать кодовым словам.

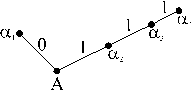
Рис. Кодовое слово непрефиксного кода