Критерий Колмогорова

Критерий Колмогорова для простой гипотезы является наиболее простым критерием проверки гипотезы о виде закона распределения. Он связывает эмпирическую функцию распределения 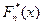с функцией распределения 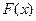непрерывной случайной величины X.

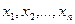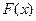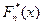Пусть - конкретная выборка из распределения с неизвестной непрерывной функцией распределения и - эмпирическая функция распределения. Выдвигается простая гипотеза H₀: 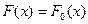(альтернативная H₁: , x R).

Сущность критерия Колмогорова состоит в том, что вводят в рассмотрение функцию

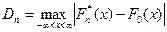, (10.2)

называемой статистикой Колмогорова, представляющей собой максимальное отклонение эмпирической функции распределения 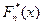от гипотетической (т.е. соответствующей теоретической) функции распределения .

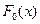Колмогоров доказал, что при 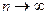закон распределения случайной величины 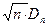независимо от вида распределения случайной величины X стремится к закону распределения Колмогорова:

,

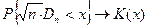где К(х) - функция распределения Колмогорова, для которой составлена таблица, ее можно использовать для расчетов уже при n ≥ 20:

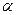
	0, 1	0,05	0,02	0,01	0,001
x0	1,224	1,358	1,520	1,627	1,950

Найдем 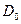такое, что .

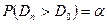Рассмотрим уравнение 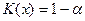. С помощью функции Колмогорова найдем корень 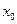этого уравнения. Тогда по теореме Колмогорова,

,

,

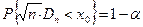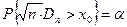откуда

.

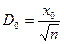Если 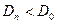, то гипотезу Н₀ нет оснований отвергать; в противном случае - ее отвергают.

Пример 10.9.Монету бросали 4040 раз (Бюффон). Получили 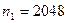выпадений герба и 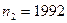выпадений решки. Проверить, используя а) критерий Колмогорова; б) критерий Пирсона, согласуются ли эти данные с гипотезой 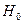о симметричности монеты .

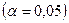Решение:

Случайная величина X принимает два значения: (решка) и х₂ = 1 (герб).

Гипотеза .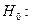

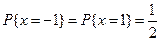а) По таблице распределения Колмогорова находим корень урав­нения 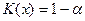при 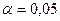. Следует 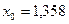. Тогда

.

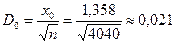Для нахождения по выборке 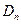строим функци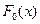и и 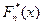и вычисляем величину

.

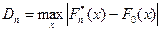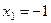
	Решка	Герб
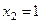
	0,5	0,5

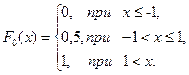
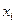
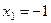
	Решка	Герб

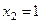
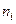
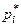
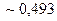
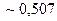
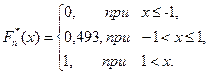
Максимальное отклонение 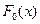от 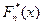равно 0,007, т.е. .

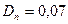Поскольку 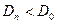, то нет оснований отвергать гипотезу 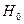. Опытные данные согласуются с гипотезой 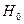о симметричности монеты.

б) Вычисляем статистику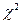

.

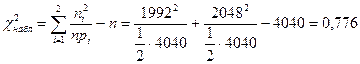По таблице 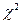-распределения находим критическую точку .

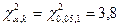Так как 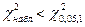, то опытные данные согласуются с гипотезой о симметричности монеты.