Определение коэффициента теплоотдачи при охлаждении заготовки

При расчете процесса конвективного теплообмена важное место занимает определение коэффициента теплоотдачи.

Сложность определения коэффициента теплоотдачи заключается в том, что он зависит от многочисленных факторов, а именно:

· природы возникновения движения;

· режима движения;

· физических свойств потока;

· форма и размеры теплоотдающей по­верхности.

По природе возникновения движения различают сво­бодное движение (естественная конвекция), возникающее под влиянием разности плотностей нагретой и холодной жидкости или газа, обусловленной разностью их тем­ператур и вынужден­ное, возникающее в результате действия како­го-либо внешнего возбудителя (ветра, вентилятора, насоса, воз­духодувной машины и т.д.).

При движении жидкости или газа различают два режима:ламинарный, характеризующийся упорядоченным спокойным, слоистым движением потока без пульсаций давления и скорости, и турбулентный, представляющий собой хаотичное движение потока, сопровождающееся пульсациями давления и скорости.

На величину коэффициента теплоотдачи существенное влияние оказывают следующие физические свойства потока: коэффициент теплопроводности l, теплоемкость с_р, плотность r, комплекс трех вышеперечисленных величин, который называется коэффициентом температуропроводности а, а также коэффициент динамической вязкости m.

Каждая поверхность создает специфические условия движения и теплообмена, поэтому форма и размеры тела, а именно они образуют ту или иную поверхность, существенно влия­ют на теплоотдачу.

Значение коэффициента теплоотдачи может быть определено аналитическим или лабораторным методом.

При аналитическом методе процесс теплоотдачи опи­сывается системой дифференциальных уравнений. Такими уравнениями для процесса теплоотдачи являются уравнение теплообмена, теплопроводности, движения и неразрывности потока. Совместное решение системы дифференциальных уравнений связано с определенными трудностями.

При лабораторном методе изготовляют экспериментальную установку, включающую оборудование для создания движения жидкости или газа, объект теплоотдачи, желательно в натуральную величину, и измерительные приборы. Лабораторный метод определения коэффициента теплоотдачи нередко связан со значительными временными и материальными затратами.

Наиболее простым способом определения коэффициента теплоотдачи является его расчет по критериальным уравнениям, которые в свою очередь являются обобщением большого числа опытных данных и решением интерполяционной задачи планирования эксперимента.

Значение критерия Нуссельта (безразмерного коэффициента теплоотдачи) определяют по уравнению

,

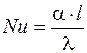где a - коэффициент теплоотдачи, Вт/м²×К; l - характерный линейный (опреде­ляющий) размер, м; l - коэффициент теплопроводности, Вт/м×К.

Значение критерия Нуссельта при поперечном обтекании воздухом цилиндрической заготовки (рис. 12) может быть рассчитано по следующим критериальным уравнениям.

Если

,

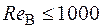то

.

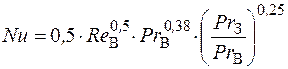Если

,

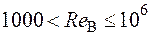то

,

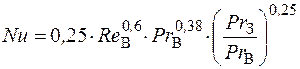где Re_В – значение критерия Рейнольдса для обтекающего заготовку воздуха; Рr_В и Рr_З – значение критерия Прандтля для обтекающего заготовку воздуха и заготовки, соответственно.

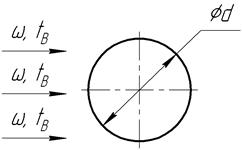
Рис. 12 – Схема обтекания воздухом цилиндрической заготовки

Значение критерия Прандтля может быть рассчитано по формуле

,

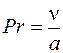где n - коэффициент кинематической вязкости воздуха при заданной температуре, м²/с; а - коэффициент температуропроводности, м²/с.

Коэффициент температуропроводности определяется выражением

,

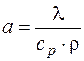где l - коэффициент теплопроводности, Вт/м×К; с_р – изобарная теплоемкость, Дж/кг×К; r - плотность, кг/м³.

Определив по критериальному уравнению значение критерия Нуссельта, можно рассчитать коэффициент теплоотдачи по формуле

.

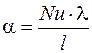При определении коэффициента теплоотдачи a в качестве определяющего размера следует принимать диаметр заготовки d.

Значение критерия Нуссельта при поперечном обтекании воздухом заготовки в форме прямоугольного параллелепипеда (рис. 13) может быть рассчитано по следующим критериальным уравнениям.

Если

,

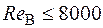то

.

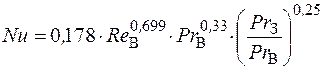Если

,

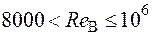то

.

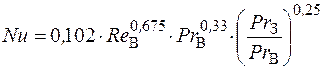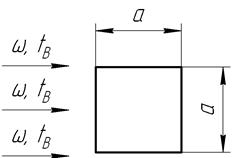
Рис. 13 – Схема обтекания воздухом заготовки