От степени ее формализации
| Ступени формализации модели | Методы использования |
| Описательная (текстовая, умозрительная) | Описание |
| Концептуальная (принципиальная) | Сравнение |
| Схематическая (графическая, алгоритмическая) | Анализ |
| Знаковая математическая (детерминированная) | Оптимизация |
| Математико-статистическая ( вероятностная) | Имитация |
Организационное моделирование на практике, по мнению автора [6], использует только три уровня моделей. Два последних представлены больше теоретическими исследованиями, правда, с их апробацией на практике [49, 53, 57].
В зависимости от характера организационных проблем, от целей, поставленных исследователями, сроков и ресурсов, выделенных для организационного проектирования или реструктуризации, квалификации разработчиков, могут быть выбраны конкретные методы организационного моделирования.
По мнению авторов [75, 115], метод организационного моделирования включает:
- графо -аналитические;
- математико-кибернетические;
- натурные;
- математико-статистические модели.
Позволим себе, основываясь на известных точках зрения специалистов, перегруппировать модели. Их классификация, по-нашему мнению, может содержать:
- текстовые и графические;
- натурные;
- математические модели.
К первой группе можно отнести все средства отображения организационных структур управления и нормативно-организационную документацию, создаваемую в процессе проектирования (рационализации) структур [18, 88].
Прежде всего, это схемы организационных структур, штатные расписания, должностные инструкции, положения о подразделениях, уставы предприятий. К ним также относятся сетевые, матричные, табличные отображения целей и функций аппарата управления, а также матрицы распределения полномочий и ответственности (линейные карты распределения ответственности, органиграммы процессов принятия решений, таблицы коэффициентов связей между функциями производства и управления).
Натурное моделирование организационных структур и процессов заключается в оценке их функционирования в реальных организационных условиях.
К методам натурного моделирования, которое в экономике весьма ограничено, могут быть отнесены:
- организационные эксперименты по перестройке структур и процессов управления в реальных организациях, т.е. заранее спланированные и контролируемые организационные изменения. Здесь уместно вспомнить эксперимент Белорусской железной дороги и его результаты, Щекинский эксперимент;
- лабораторные эксперименты - искусственно созданные ситуации принятия решений в области организационного проектирования и новаторства;
- управленческие (деловые) игры, которые связаны с разрешением реальных или гипотетических организационных ситуаций.
И если лабораторные эксперименты, и эксперименты в реальных условиях деловой жизни не достаточно распространены, то увлечение деловыми играми было достаточно сильным в 70 - 80 годы.
К математическим моделям можно отнести математико-статистические модели зависимостей между исходными факторами организационных систем и характеристиками организационных структур. Например, регрессионные модели зависимости численности ИТР и служащих от производственно-технических характеристик организации, детально разработанные в свое время учеными НИИ труда [80,115]. Общая формула для расчета численности управленцев по i - той функции имеет следующий вид:
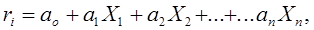
где 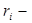 нормативная численность работников управления по i - той функции;
нормативная численность работников управления по i - той функции; 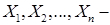 значения факторов, определяющих численность работников по данной функции;
значения факторов, определяющих численность работников по данной функции; 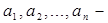 коэффициенты регрессии (показатели степени или коэффициенты), определяющие степень влияния каждого фактора на численность работников;
коэффициенты регрессии (показатели степени или коэффициенты), определяющие степень влияния каждого фактора на численность работников; 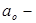 постоянный коэффициент уравнения нормативной зависимости.
постоянный коэффициент уравнения нормативной зависимости.
В методических указаниях НИИ труда по построению аппарата управления на предприятиях и в производственных объединениях, кроме нормативов численности для определения внутренней структуры управленческих подразделений, разработаны корреляционные зависимости следующего вида:
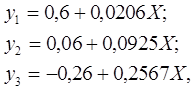
где 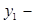 число заместителей начальников отдела;
число заместителей начальников отдела; 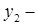 количество бюро в отделе (число начальников бюро);
количество бюро в отделе (число начальников бюро); 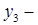 количество групп (число старших исполнителей);
количество групп (число старших исполнителей);  численность работников отдела, чел.
численность работников отдела, чел.
Кроме этих зависимостей, на основе математической статистической статистики в НИИ труда были разработаны модели для определения норм управляемости, модели нормативных коэффициентов централизации по функциям управления и формулы для расчета уровней линейного и функционального руководства на предприятиях [88].
Задача разработки и внедрения корреляционно - регрессионных моделей ставилась и решалась для определения нормативов численности не только для предприятий и объединений, но и для других организационных систем, например, для НИИ и КБ [82] и министерств [19].
Таким образом, подход к формированию структур управления, основанный на методе аналогий и нормативах численности, в прошлые десятилетия получил довольно широкое внедрение в организационную практику. Но эффект от применения этого подхода, как показала практика, был весьма низок. Основываясь на "прошлом" опыте, этот подход не содержал собственных методов формирования рациональных структур.
Кроме регрессионных моделей, многие специалисты в области формализации организационных структур предлагают использовать для анализа и синтеза структур группу оптимизационных моделей.
Выбор параметров организационной структуры в таких моделях производят, исходя из условий оптимизации некоторого показателя, характеризующего эффективность функционирования организации.
Так, авторами [34] решается задача синтеза организационной структуры методами теории массового обслуживания.
В работе производится описание синтеза структуры, которая заключается в наращивании системы управления снизу вверх субоптимальными уровнями. Эта процедура позволяет найти число уровней иерархии, количество блоков на каждом уровне, а также состав блоков каждого уровня.
Теория массового обслуживания использована и в [81] для описания процесса функционирования организации. Каждая группа задач, решаемая аппаратом управления, реализуется функциональным блоком. В качестве критерия оптимальности организационной структуры в модели выступает сумма приведенных затрат на создание и эксплуатацию системы управления, потерь от запаздывания выработки оптимальных управленческих решений, задержек принятия и согласования оперативных решений.
Варианты организационной структуры отличаются вариантами исполнения отдельных звеньев. Каждому варианту исполнения того или иного звена сопоставляется переменная 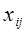 . Ее значение равно 1, если j - й вариант исполнения i - го звена принимается, и 0 в противном случае;
. Ее значение равно 1, если j - й вариант исполнения i - го звена принимается, и 0 в противном случае; 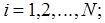
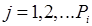 . Выражая слагаемые целевой функции через переменные
. Выражая слагаемые целевой функции через переменные 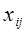 , авторы формулируют следующую задачу поиска оптимальной структуры: найти такие значения
, авторы формулируют следующую задачу поиска оптимальной структуры: найти такие значения 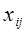 , при которых показатель w принимает минимальное значение и выполняются ограничения на максимально допустимые эксплуатационные расходы, капитальные затраты и численность персонала.
, при которых показатель w принимает минимальное значение и выполняются ограничения на максимально допустимые эксплуатационные расходы, капитальные затраты и численность персонала.
В ряде случаев при построении структуры необходимо решить задачи оптимального обеспечения организации различного рода ресурсами. Так, в [11] приводится модель определения рационального состава работников подразделения НИИ с использованием аппарата динамического программирования.
Вводятся показатели перерасхода зарплаты на одного сотрудника по категориям, возникающего при неправильном комплектовании штатов. Требуется определить, каким должен быть кадровый состав подразделения, чтобы средний перерасход заработной платы был минимальным.
Приведем еще один пример постановки оптимизации организационной структуры, данный в [58].
В работе рассматривается множество из N элементов, каждый из которых описывается входной переменной 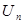 и входной переменной
и входной переменной 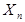 ,
, 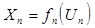 , n = 1,2,...,N. Элементы могут объединяться в систему с произвольной организационной структурой, которая определяется числом уровней иерархий, составом элементов каждого уровня, их соподчиненностью. Если элемент с номером
, n = 1,2,...,N. Элементы могут объединяться в систему с произвольной организационной структурой, которая определяется числом уровней иерархий, составом элементов каждого уровня, их соподчиненностью. Если элемент с номером 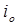 непосредственно руководит функционированием элементов с номерами
непосредственно руководит функционированием элементов с номерами 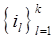 , то
, то
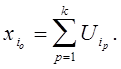
В случае, когда для некоторого элемента отсутствует вышестоящий, значение его входа полагается равным нулю. Определен показатель качества функционирования системы
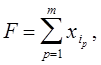
где 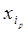 - выходы элементов нижнего уровня, которые непосредственно осуществляют производство "продукции". Выделяются две задачи. При заданной организационной структуре можно поставить задачу оптимизации действия, заключающуюся в максимизации F по отношению к принимаемым решениям
- выходы элементов нижнего уровня, которые непосредственно осуществляют производство "продукции". Выделяются две задачи. При заданной организационной структуре можно поставить задачу оптимизации действия, заключающуюся в максимизации F по отношению к принимаемым решениям 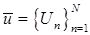 . Рассматривая системы с оптимальными
. Рассматривая системы с оптимальными 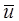 при разных организационных структурах, можно поставить задачу оптимизации структуры системы.
при разных организационных структурах, можно поставить задачу оптимизации структуры системы.
Построение оптимизационных моделей, безусловно, является одним из эффективных направлений развития формальных методов построения и рационализации организационных структур. Но трудности, возникающие при применении методов оптимизации, обусловили немногочисленность теоретических разработок и ограничили их результаты, в основном, постановками задач, носящих абстрактный характер.
Более многочисленными являются модели, в которых выбор параметров структур осуществляется, исходя из косвенных критериев, характеризующих процесс функционирования организации. При этом предполагается, что организационная структура должна создавать нормальные условия для реализации этого процесса.
В третью группу моделей можно включить модели построения организационных структур на основе косвенных критериев оценки их качеств. В свою очередь, эта группа может быть разделена на несколько подгрупп.
В первую входят модели, в которых задача оптимизации определенных характеристик ставится как задача разбиения некоторого множества А на классы, обладающие требуемыми свойствами. Приведем несколько примеров подобных моделей.
В [24] ставится задача построения такой организационной структуры, которая позволяет оптимизировать потоки информации на уровне подразделений. Для этого выделяется множество задач и информационные связи между ними. Требуется, учитывая ряд ограничений, найти такое разбиение полученного неориентированного графа, при котором число связей внутри подграфов будет максимальным.
В [68] предлагается модель рационализации средних звеньев управления. На основе корреляционной матрицы связи задач ищется наилучший вариант их распределения по подразделениям. При этом применяется аппарат факторного анализа.
Во вторую подгруппу входят модели, по которым расчет производится в два этапа: на первом по определенному правилу группируются элементы исходного множества, на втором - параметры организационной структуры с учетом принятого критерия и ограничений. Первая модель предлагается, например, для формирования организационной структуры производственного участка [23]. В соответствии с ней совокупность комплексов однородных деталей разбивается на такие подгруппы, которые позволили бы загрузить оборудование в пределах нормы с минимальным временем переналадки. Вторая модель этой группы предназначена для распределения задач по подразделениям. На первом этапе решения предлагается группировать все задачи в классы, близкие по своему содержанию, на втором этапе - максимизируется суммарная эффективность использования подразделений для решения выделенных групп задач при ограничениях на их пропускную способность.
Более совершенными по сравнению с рассмотренными моделями являются модели третьей подгруппы, в которых производится иерархическая группировка элементов множества [55, 56, 75, 77]. Так, в [55] приводится модель выявления рациональных сфер деятельности в структурных звеньях планирующей организации. Предполагается, что необходимость координации обусловлена в основном взаимосвязями соответствующих элементов объектов планирования, которые должны найти отражение в однородности данных, используемых при решении задач. Поэтому группировка на основе сходства учитываемой информации будет приводить к выделению блоков задач, требующих первоочередного согласования. Считаются известными множества плановых задач и информационные связи между ними, а также используемые при их решении показатели, полученные вне данной организации ( n, m - соответственно, количество задач и внешних показателей).
Каждую задачу предлагается описывать набором 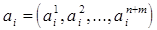 , где
, где 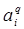 соответствует показателю
соответствует показателю 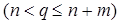 или задаче
или задаче 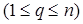 и принимает значения 1 или 0 в зависимости от того, используется ли q - й показатель или результаты выполнения q - й задачи при решении i - й или нет (
и принимает значения 1 или 0 в зависимости от того, используется ли q - й показатель или результаты выполнения q - й задачи при решении i - й или нет ( 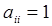 по определению). На множестве пар наборов вводится мера близости
по определению). На множестве пар наборов вводится мера близости 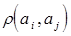 , которая отражает степень их сходства и, по предположению, потребность в координации решения соответствующих плановых задач.
, которая отражает степень их сходства и, по предположению, потребность в координации решения соответствующих плановых задач.
В четвертую группу объединены разные по характеру модели [26,53,112].
Рассмотрим модель, предлагаемую в [112]. Основным параметром, характеризующим организационную структуру, в этой модели принята экономическая ответственность.
Экономическая ответственность - мера соотношения между деятельностью в отдельной вершине иерархии и общими итогами деятельности организации. При этом экономическая ответственность рассматривается в модели как ожидаемый вклад вершины в общий итог работы, не зависящий от конкретных свойств работника или группы работников, действующих в этой вершине. Предполагается, что заработная плата сотрудников должна зависеть от характера и меры их взаимодействия, вклада в общий итог работы. Это позволяет подойти к определению меры экономической ответственности с учетом взаимодействия сотрудников и системы оплаты их труда.
При равном диапазоне контроля на всех уровнях иерархии модель представляет собой систему конечно-разностных уравнений вида:
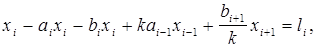
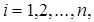
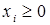 ,
, 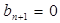 ,
, 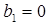
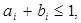
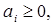
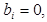
где 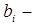 зарплата работника i - го уровня;
зарплата работника i - го уровня;
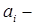 параметр контроля, выражающий уровень вмешательства работника (i + 1) - го уровня в деятельность работника i - го уровня;
параметр контроля, выражающий уровень вмешательства работника (i + 1) - го уровня в деятельность работника i - го уровня;
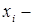 трактуется как экономическая ответственность работника i - го уровня.
трактуется как экономическая ответственность работника i - го уровня.
Модель можно использовать для анализа соответствия 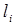 (выражающего реальную ответственность) и
(выражающего реальную ответственность) и 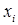 и обоснования направлений совершенствования организационной структуры.
и обоснования направлений совершенствования организационной структуры.
Рассмотрим кратко еще два подхода к моделированию организационных структур управления [2, 6, 5].
В работе [5] предлагается методика проектирования организационной структуры предприятия путем определения трудоемкости взаимодействия производственных подразделений, технических и функциональных служб предприятия.
Основное внимание в этой монографии уделяется моделированию организационных структур для оптимизации и распределения ресурсов между звеньями структуры и установления между ними связей для выполнения поставленных задач. При этом за базу берется производственная структура.
В основе математического моделирования лежит описание организационной структуры на основе формализации ее элементов вначале как вершин графа, а связей между ними - как графа. Затем для элементов производственной структуры формулируются задачи оптимизации их функционирования, а связывают их оптимальные решения к оценке ресурсов, услуг и полуфабрикатов. Стохастический характер связей между элементами структуры системы управления требует ее рассмотрения как многофазной иерархической системы массового обслуживания.
В этой же работе [5] излагаются принципы имитационного моделирования организационных структур, основанные на статистических закономерностях изменения материальных и информационных потоков. Последовательность проектирования структуры, предложенная автором, не вызывает возражения, т.к. вначале предлагается организовать материально-энергетические потоки в производстве, а затем сеть коммуникаций в управлении.
В качестве основного критерия формирования организационных структур Л.А. Базилевич предлагает использовать принцип наименьшего взаимодействия, заключающийся в том, что в сложной многоуровневой системе управления, рассматриваемой как совокупность подсистем, обладающих относительной автономией, целесообразность поведения этих подсистем проявляется в минимизации взаимодействия между ними так, что в устойчивых состояниях эти подсистемы функционируют независимо, автономно.
К исследованиям Л.А. Базилевича близки исследования, изложенные в монографии "Анализ и формирование организационной структуры промышленного предприятия" [2]. В ней главным критерием "нужности" организационного звена является теснота деловых связей этого звена с другими элементами структуры. Наряду с анализом организационной структуры управления ведется анализ производственной структуры.
Порядок проведения работ в предлагаемой методике представлен укрупненной блок-схемой на рис.1.33.
|

Анализ Анализ
Дата добавления: 2019-02-07; просмотров: 485;
