Методы вычисления коэффициентов Клебша-Гордана

Обозначим полную ВФ .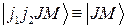

Тогда можем записать 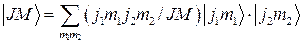(2.5.1).

Применим к обеим частям равенства (2.5.1) оператор проекции полного момента 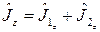. Собственные значения оператора проекции полного момента 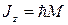, то есть имеет место операторное равенство .

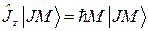Тогда

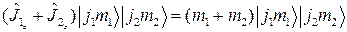(2.5.2),

то есть, как мы уже знаем, коэффициенты 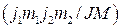отличны от нуля только при 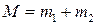и суммирование в формуле (2.5.1) фактически производиться либо по 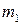, либо по .

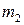Существуют три метода вычисления коэффициентов КГ (если не считать возможности взять их из таблиц).

Первый – это метод последовательного спуска.

Начнем с

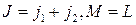(2.5.3).

В этом случае имеем

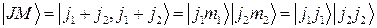(2.5.4).

Подействуем оператором 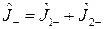на функцию (2.5.4).

Оператор 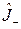- оператор понижения, он действует на состояние с квантовым числом 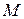и переводит его в состояние с квантовым числом 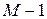, то есть имеет место операторное равенство

,

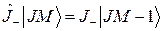где 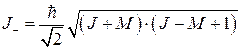- собственные значения оператора понижения .

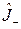Следовательно,

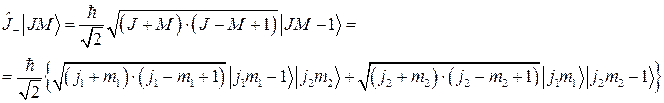
Используя условия (2.5.3), получим:

,

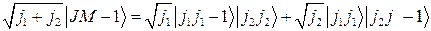или

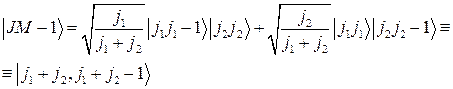(2.5.5).

Есть еще одна собственная функция, принадлежащая собственному значению 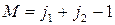, она соответствует .

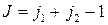Поскольку она должна быть ортогональна к функции (2.4.5), мы имеем

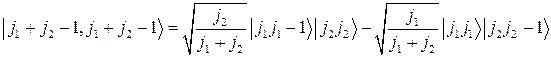(2.5.6).

Теперь можно подействовать на обе части равенств (2.5.5) и (2.5.6) понижающими операторами и получить новые линейные комбинации для 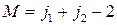и так далее.

Второй метод принадлежит Рака, который получил замкнутую формулу

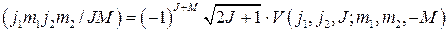(2.5.7),

где

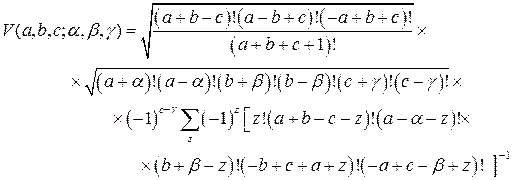(2.5.8).

Здесь 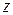пробегает все целочисленные значения до тех пор, пока аргументы всех факториалов остаются неотрицательными.

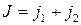, следовательно, формулы (2.5.7) и (2.5.8) примут вид

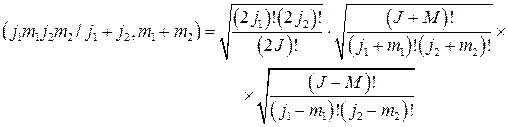(2.5.9).

Третий метод вычисления коэффициентов КГ – это метод проекционного оператора.

Определим проекционный оператор равенством

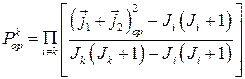(2.5.10).

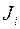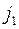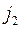Произведение содержит здесь все значения (которые могут получиться от сложения и ), кроме того, для которого мы ищем коэффициент.

Равенство (2.4.1) можно обратить, полагая

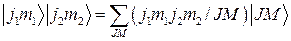(2.5.11).

Ограничение 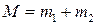, как и прежде, приводит к тому, что суммирование фактически производится только по одному индексу .

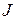Действуя на обе части равенства (2.5.11) проекционным оператором 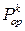, мы обратим в нуль все члены ряда, кроме 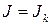. Таким образом, получаем

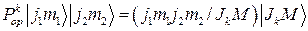(2.5.12).

Вследствие унитарности преобразования

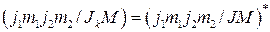(2.5.13)

Подставляя соотношения (2.5.1) и (2.5.13) в формулу (2.5.12), находим

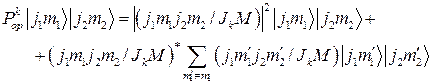(2.5.14).

Таким образом, действуя проекционным оператором 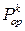на функцию 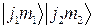, мы получаем ряд, среди членов которого содержится и .

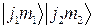Разделив этот ряд на квадратный корень из коэффициентов при 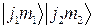, мы получим разложение для 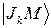с должными коэффициентами Клебша – Гордана.

Модуль №3 " Различные приложения квантовой теории момента количества движения"