Критерии согласия относительно закона распределения.
При проверке статистических гипотез не всегда есть основание высказать альтернативную гипотезу в явном виде. Часто имеется в виду просто невыполнение основной гипотезы.
В этом случае требуется выяснить, согласуются ли данные с основной гипотезой или противоречат ей. Критерии, которые позволяют это сделать, называют критериями согласия.
Анализируя выборочные данные: эмпирические частоты и гистограмму (или полигон), можно высказать предположение о виде закона распределения генеральной случайной величины Х.
При этом в виду ограниченного числа наблюдений, опытный (эмпирический) закон распределения будет в какой - то мере отличаться от предполагаемого, даже если предположение о законе распределения сделано правильно.
В связи с эти возникает необходимость решать следующую задачу: является ли расхождение между опытным и предполагаемым законами распределения следствием ограниченного числа опытов, или оно является существенным и истинное распределение отличается от предполагаемого.
Для окончательного решения вопроса о виде закона распределения в подобных случаях представляется целесообразным проверить, насколько сделанное предположение согласуется с опытом.
Так как все предположения о виде теоретического распределения – это гипотезы, а не категорические утверждения, то они, естественно должны быть подвергнуты статистической проверке с помощью критериев согласия относительно закона распределения.
Критерии согласия, опираясь на установленный закон распределения, дают возможность установить, когда расхождение между эмпирическими и теоретическими частотами следует признать несущественными (случайными), а когда – существенными (неслучайными).
Таким образом, критерии согласия позволяют отвергнуть или подтвердить правильность выдвинутой гипотезы о виде распределения в эмпирическом ряду и дать ответ, можно ли принять для данного эмпирического распределения модель, выраженную некоторым теоретическим законом распределения.
Существует ряд критериев согласия проверки гипотезы о виде распределения.
Критерий согласия c2 (хи-квадрат) Пирсона является одним из основных статистических критериев. Этот критерий был предложен английским математиком Карлом Пирсоном (1857 – 1936) для оценки существенности расхождения между частотами эмпирического и теоретического распределений.
Сформулируем постановку задачи. Дана выборка (Х1 , Х2 , ... , Хn ) объёма n. Основная гипотеза состоит в том, что эта выборка произведена из совокупности, имеющей некоторое заданное распределение.
Основная гипотеза может быть простой (т.е. функция распределения определена однозначно) или параметрической (функция распределения зависит от к неизвестных параметров).
Процедура проверки гипотезы о виде распределения с помощью критерия c2 Пирсона состоит из 5 этапов.
1. Весь диапазон значений генеральной случайной величины Х разбивают на интервалы: D1 , D2 , ... , Dm без общих точек и подсчитывают число наблюдений, попавших в каждый интервал (интервалы выбирают так, чтобы в каждый попало не менее 5 наблюдений).
2. Предположив справедливость основной гипотезы, подсчитывают вероятность попадания в каждый интервал:
pi=P {XÎDi |H0 } ; i=1, 2, …, m.
При проверке параметрической гипотезы о виде распределения параметры распределения оказываются неизвестными, поэтому их заменяют наилучшими оценками по имеющейся выборке.
3. Составляют статистику критерия:
.
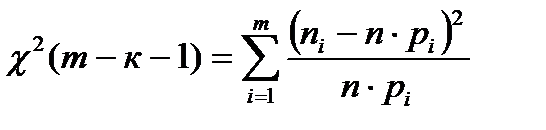Здесь к – число неизвестных параметров распределения.
Обоснуем выбор статистики. Относительная частота попадания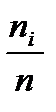 
в интервал Di - является состоятельной оценкой для pi - вероятности попадания в этот интервал (согласно закону больших чисел). Таким образом, если проверяемая гипотеза истинна, то разность 
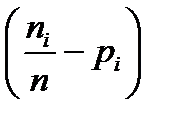должна быть мала, следовательно, и вся сумма должна быть мала. Следовательно, если значение статистики велико, то гипотезу надо отвергнуть. Таким образом, статистика критерия характеризует отклонение теоретических данных от гипотетических.
4. Задавшись уровнем значимости (то есть вероятностью отвергнуть основную гипотезу, если на самом деле она верна) a, строят критическую область, используя следующую предельную теорему.
Теорема Пирсона: при выполнении основной гипотезы распределение статистики критерия сходится к c2 распределению с m – к – 1 степенью свободы.
Критическая область – это область больших значений статистики критерия. Критическое значение – c2кр - квантиль уровня 1-a распределения c2 с m – к – 1 степенью свободы.
5. Если значение статистики критерия меньше критического значения:
c2 (m–к – 1) < c2кр ,
то гипотезу принимают. В этом случае говорят, что выборочные данные согласуются с гипотезой или не противоречат ей.
Если значение статистики критерия больше (или равно) критическому значению:
c2 (m – 1) ≥ c2кр ,
то гипотезу отвергают. В этом случае говорят, что выборочные данные не согласуются с гипотезой или противоречат ей.
Приведём небольшую таблицу для определения критических значений критерия c2 Пирсона при двух заданных уровнях значимости.
| Уровень значимости | Число степеней свободы | ||||||||
| 0,05 | 3,84 | 5,99 | 7,82 | 9,49 | 11,1 | 14,1 | 16,9 | 19,7 | 25,0 |
| 0,01 | 6,64 | 9,21 | 11,3 | 13,3 | 15,1 | 18,5 | 21,7 | 24,7 | 30,6 |
При использовании данной методики требуется, чтобы объём выборки n>50.
Дата добавления: 2018-11-25; просмотров: 636;