Термодинамический процесс

Один из постулатов термодинамики формулируется так: термодинамическая система стремится перейти в состояние равновесия, в котором может находиться сколь угодно долго при отсутствии внешнего воздействия на нее.

Если на систему оказывается какое-либо внешнее воздействие, приводящее к обмену между системой и окружающей средой веществом или энергией, то система перейдет в другое состояние равновесия, характеризующиеся другим набором параметров. Переход системы из одного состояния равновесия в другое называется термодинамическим процессом. В ходе процесса обязательно изменяется хотя бы один из параметров системы.

Процесс при постоянной температуре (Т=const) называется изотермическим, при постоянном объеме (V=const) – изохорический(или изохорный), при постоянном давлении (р=const) – изобарический (или изобарный).

Процесс, в котором система возвращается в исходное состояние, называется круговым или циклическим.

Химический процесс, являющийся, по сути, совокупностью химических реакций, протекает с изменением количеств веществ. Пусть система, состоящая из вещества А, находится в состоянии термодинамического равновесия 1. При добавлении в эту систему вещества В (воздействие на систему извне) она должна перейти в новое состояние равновесия. Одним из путей перехода является химическая реакция между веществами А и В с образованием продуктов C и D:

n_аA + n_bB ® n_сC + n_dD.

Если между веществами C и D протекает реакция с образованием веществ А и В: n_сC + n_dD®n_аA + n_bB, то в состоянии равновесия 2 термодинамическая система будет состоять из смеси веществ A, B, C и D в соответствующих количествах. Химическая реакция запишется следующим образом:

n_аA + n_bB« n_сC + n_dD.

Если на данную систему было оказано воздействие извне (обмен энергией или веществом), то это приведет к переходу системы в состояние равновесия 3 с другим количеством веществ A, B, C и D. Причем, неочевидно, в каком направлении будет протекать химическая реакция, приводящая систему в состояние равновесия 3. Условились считать, что реакция протекает в прямом направлении, если количество исходных веществ (в нашем случае А и В) уменьшается, а количество продуктов реакции (в нашем случае C и D) увеличивается. Говорят, что реакция протекает в обратном направлении, если увеличивается количество исходных веществ при соответствующем уменьшении количества продуктов. Если реакция в системе может протекать в прямом и обратном направлении, то говорят, что она обратимая.

Очевидно, что для обратимых реакций «исходные реагенты и продукты реакции» – понятия условные и зависят от того, как записана реакция. При изменении записи химической реакции они меняются:

Процессы бывают самопроизвольными и несамопроизвольными (вынужденными). Самопроизвольные – процессы, для протекания которых не требуются затраты энергии из окружающей среды. Примеры – переход теплоты от нагретого тела к холодному или процесс смешения газов. Несамопроизвольные – процессы, для протекания которых необходимы затраты энергии из окружающей среды. Пример – разделение газовых смесей.

По характеру перехода термодинамической системы из одного состояния равновесия в другое процессы делятся наравновесные (обратимые) и неравновесные (необратимые).

Равновесный (обратимый) процесс представляет собою бесконечную последовательность отдельных состояний равновесия. Система как бы все время находится в состоянии равновесия (квазистатический процесс). Его можно в любой момент заставить протекать в обратном направлении по тому же самому пути, изменив какой-либо параметр на бесконечно малую величину. Очевидно, что если время перехода системы в новое состояние равновесия (t) будет много меньше, чем время воздействия на систему (t) (t<< t), то можно считать, что в каждый момент времени система будет находиться в термодинамическом равновесии, что и является условием обратимости процесса. Такие процессы суть идеализация реальных процессов, экспериментально к ним можно только приблизиться, но никогда нельзя достигнуть. Если равновесный процесс провести сначала в прямом направлении, а затем в обратном, то система пройдет через те же состояния равновесия и не обнаружится никаких изменений, как в самой системе, так и в окружающей среде. Работа, совершаемая системой в прямом процессе (W₁₂), будет равна работе, необходимой для возврата системы в исходное состояние (W₂₁). Работы прямого и обратного процесса равны по абсолютной величине и противоположны по знаку: W₁₂=–W₂₁ (условие термодинамической обратимости процесса).

В неравновесных (необратимых) процессах время перехода системы в состояние равновесия много больше, чем время воздействия на систему (t >> t). Поэтому в системе не устанавливается термодинамическое равновесие в промежуточных стадиях, и они не совпадают при прямых и обратных переходах. Работа, совершаемая системой в неравновесныхпроцессах при переходе из одного состояния равновесия в другое (W₁₂) не равна работе необходимой для возврата системы в исходное состояние (W₂₁). Если система совершала работу в прямом процессе, то для ее возврата в исходное состояние требуется бόльшая работа: W₁₂< W₂₁. Если в прямом процессе внешние силы совершали работу над системой, то при возвращении в исходное состояние термодинамическая система совершит меньшую работу: W₁₂>W₂₁. Отметим, что работа совершаемая системой и термодинамически обратимостимых процессах является максимально возможной.

Пример.Процесс изотермического расширения идеального газа.

Начальное (первое) состояние системы: идеальный газ при температуре Т находится под поршнем, нагруженным тремя гирями (рис.5.2), давление в системе р₁, занимаемый объем V₁. Конечное (второе) состояние системы: идеальный газ при температуре Т находится под разгруженным поршнем, давление в системе р₂, занимаемый объем V₂. Работа, совершаемая идеальным газом при переходе из первого состояния во второе, зависит от характера воздействия на систему. В случае бесконечно медленного снятия нагрузки с поршня (t<< t) система все время находится в состоянии равновесия, которое описывается уравнением Менделеева-Клапейрона. В этом случае элементарная работа, совершаемая системой, равна:

.

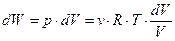Рис. 5‑2 Процесс расширения (1-2) и сжатия (2-1) идеального газа

Тогда работы при переходе системы из состояния 1 в состояние 2, и обратно из 2 в 1 , равны по величине и противоположны по знаку:

,

,

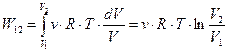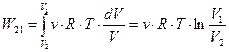W_равн =½W₁₂½ = ½W₂₁½.

Работа, совершаемая при переходе системы из одного состояния в другое, равна площади под кривой, описывающей этот переход, в координатах р-V (рис. 5.2).

В случае ступенчатого перехода системы из состояния 1 в состояние 2 (время разгрузки системы меньше, чем время установления равновесия в системе – t >> t) работа, совершаемая идеальным газом меньше, чем при реализации того же процесса в равновесных условиях (площадь под ломаной линией меньше): W₁₂ < W_равн. При проведении процесса в обратном направлении в этих же условиях W₂₁ > W_равн.