Зонная модель кристаллического тела
Электропроводность (электрическая проводимость, проводимость) – способность вещества проводить электрический ток под действием электрического поля. Она обусловлена присутствием свободных носителей заряда в твердом теле, направленное движение которых и есть электрический ток. Электропроводность (s) определяется величиной заряда носителя тока (q), его подвижностью (m) и концентрацией носителей (n):
s = q×m×n.
По механизму, величине и температурной зависимости электропроводности твердые тела классифицируют на металлы, полупроводники и диэлектрики.
Металлы имеют при комнатной температуре высокую электропроводность (s = 104 ÷ 106 Ом-1×см-1), которая уменьшается с ростом температуры. Диэлектрики из-за отсутствия носителей заряда при обычных условиях обладают низкой проводимостью (s = 10-8 ÷ 10-18 Ом-1×см-1). Полупроводники по величине электропроводности занимают промежуточное положение (s = 10-8 ÷ 104 Ом-1×см-1), электропроводность увеличивается с ростом температуры.
В металлах и полупроводниках электропроводность обусловлена подвижностью электронов. Для описания механизма переноса заряда должны быть использованы модели химической связи в кристаллах. Причем для каждого отдельного типа кристалла должны быть использованы свои модели (металлическая связь, ковалентная связь и т.д.).
В рамках физики твердого тела была разработана зонная модель твердого тела, позволяющая с единой позиции описать поведение электронов во всех типах кристаллов. В результате решения квантово-механической задачи об энергетических состояниях электрона в кристалле (уравнение Шрёдингера для кристалла) были сформулированы следующие основные положения.
В системе из N изолированных атомов имеются разрешенные энергетические состояния, которые N-кратно вырождены (одинаковые по энергии для всех атомов). В кристалле, вследствие взаимодействия между атомами, вырождение снимается, энергетические состояния будут отличаться друг от друга. В результате в кристалле возникает система, состоящая из N различных близкорасположенных энергетических уровней, которые образуют энергетические зоны. Эти зоны отделены друг от друга запрещенными зонами (области значений энергий, которые не могут принимать электроны).
На каждом энергетическом уровне согласно принципу Паули может находиться не более двух электронов. Поэтому, если в зоне все уровни заселены электронами, их перемещение невозможно. В то же время, если имеются свободные, незанятые уровни, электрон может свободно переходить с одного уровня на другой. Наивысшая из разрешенных зон, в которой при температуре 0 К все энергетические состояния заняты, называется валентной зоной. Свободная или частично заполненная верхняя разрешенная энергетическая зона называется зоной проводимости.
К аналогичным положениям можно прийти, используя метод молекулярных орбиталей для описания химической связи в кристалле. Согласно методу МО каждый электрон принадлежит всей молекуле и движется в поле всех ядер и электронов. В методе МО оперируют понятием молекулярных орбиталей, которые получают в результате сложения и вычитания атомных орбиталей. Число молекулярных орбиталей всегда равно числу атомных орбиталей АО, взятых для их построения. Заселение электронами молекулярных орбиталей происходит с выполнением тех же принципов, что и заселение АО (принцип минимума энергии, принцип Паули, правило Хунда).
Кристалл можно рассмотреть как макромолекулу, состоящую из N-атомов. В этом случае кристалл будет иметь N молекулярных орбиталей, совокупность которых образует систему энергетических зон, аналогичную полученной из зонной модели.
 Если кристалл образован из N одинаковых атомов, имеющих s и p атомные орбитали, то образуется система, состоящая из s-зоны МО, содержащей N s АО, и р-зоны МО, содержащей 3N p АО (рис. 4.11).
Если кристалл образован из N одинаковых атомов, имеющих s и p атомные орбитали, то образуется система, состоящая из s-зоны МО, содержащей N s АО, и р-зоны МО, содержащей 3N p АО (рис. 4.11).
Рис. 4‑11 Построение энергетических зон при последовательном присоединении атомов
Энергетические зоны характеризуются понятиями ширина зоны и заселенность. Ширина зоны равна разности максимального и минимального значений энергий МО, входящих в зону. Она определяется природой атомов и межатомным расстоянием, но не зависит от N. Для реальных кристаллов ширина зон составляет величину порядка нескольких электрон-вольт. Поэтому при N ~ 1023 (количество вещества порядка одного моля) разница энергий между уровнями в зоне ~10-23 эВ. Если уровни не заняты, электроны могут свободно переходить с одного уровня на другой в пределах зоны, поскольку энергия электрона при T=300 К составляет величину порядка 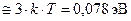 , что несоизмеримо больше различия в энергии между уровнями. Такие электроны обычно называют свободными, при приложении электрического поля именно они определяют электропроводность вещества, участвуя в переносе заряда.
, что несоизмеримо больше различия в энергии между уровнями. Такие электроны обычно называют свободными, при приложении электрического поля именно они определяют электропроводность вещества, участвуя в переносе заряда.
Свойства твердых тел с позиций зонной теории определяются взаимным расположением зон и их заселенностью, то есть количеством электронов в зоне. В зависимости от строения электронных оболочек атомов кристалла и типа химической связи между ними образующиеся энергетические зоны могут быть полностью или частично заселены электронами. Полностью заполненная зона представляет собой валентную зону, а свободная или частично заполненная – зону проводимости. Энергетическая разность между максимальным по энергии уровнем валентной зоны (EV – верх валентной зоны) и нижним уровнем зоны проводимости (EC – дно зоны проводимости) называется шириной запрещенной зоны (Eg = EC – EV).
Распределение электронов по энергетическим состояниям.
Вероятность заселения электронами энергетических состояний в кристалле (р) описывается функцией распределения Ферми-Дирака:
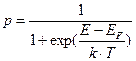 ,
,
где E – энергия электронного уровня; EF – энергия Ферми; k – константа Больцмана.
 При абсолютном нуле, согласно принципу минимума энергии и принципу Паули, все энергетические состояния ниже какого-то уровня заняты (вероятность их заполнения р=1), а состояния, расположенные по энергии выше, свободны (вероятность их заполнения р=0). Граница заселения энергетических уровней называется уровнем Ферми (энергия Ферми – EF). С повышением температуры вследствие теплового возбуждения часть электронов переходит из состояний, лежащих ниже уровня Ферми, в состояния с энергией, превышающий уровень Ферми. Это приводит к «размыванию» первоначальной функции распределения состояний. Необходимо отметить, что число электронов выше уровня Ферми (в зоне проводимости) и свободных уровней ниже уровня Ферми (в валентной зоне) одинаково. Их распределение по энергии зеркально симметрично (рис.4.12).
При абсолютном нуле, согласно принципу минимума энергии и принципу Паули, все энергетические состояния ниже какого-то уровня заняты (вероятность их заполнения р=1), а состояния, расположенные по энергии выше, свободны (вероятность их заполнения р=0). Граница заселения энергетических уровней называется уровнем Ферми (энергия Ферми – EF). С повышением температуры вследствие теплового возбуждения часть электронов переходит из состояний, лежащих ниже уровня Ферми, в состояния с энергией, превышающий уровень Ферми. Это приводит к «размыванию» первоначальной функции распределения состояний. Необходимо отметить, что число электронов выше уровня Ферми (в зоне проводимости) и свободных уровней ниже уровня Ферми (в валентной зоне) одинаково. Их распределение по энергии зеркально симметрично (рис.4.12).

Рис. 4‑12 Распределение электронов по энергетическим состояниям для металлов
В кристаллах, имеющих небольшую ширину запрещенной зоны, возможен переход электронов из валентной зоны в зону проводимости вследствие их теплового возбуждения, с образованием в валентной зоне свободного энергетического состояния (уровня), получившего название – дырка (рис.4.13).

Рис. 4‑13 Образование в кристалле электронно-дырочных пар. ē − электрон проводимости; p+ − дырка
Вероятность этого перехода зависит от ширины запрещенной зоны (Eg) и температуры. При относительно высоких температурах (E – EF)>>k×T, 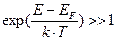 , функцией распределения приобретает вид
, функцией распределения приобретает вид 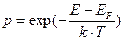 . Так как уровень Ферми находится в середине запрещенной зоны:
. Так как уровень Ферми находится в середине запрещенной зоны: 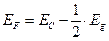 , то для E = EC →
, то для E = EC → 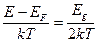 . Таким образом, вероятность перехода электронов из валентной зоны в зону проводимости, будет определять функция:
. Таким образом, вероятность перехода электронов из валентной зоны в зону проводимости, будет определять функция:
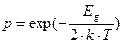 .
.
Дата добавления: 2017-02-20; просмотров: 1163;
