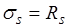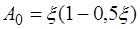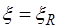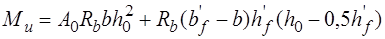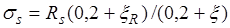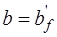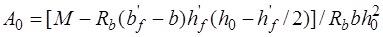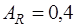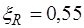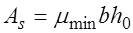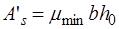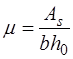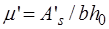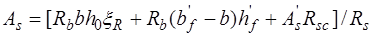ТИПЫ ЗАДАЧ, ВСТРЕЧАЮЩИЕСЯ ПРИ РАСЧЕТЕ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ НОРМАЛЬНОГО СЕЧЕНИЯ ТАВРОВОЙ И ДВУТАВРОВОЙ ФОРМЫ С НЕНАПРЯГАЕМЫМ АРМИРОВАНИЕМ
При расчете тавровых сечений встречаются следующие типы задач: а) известны размеры сечения 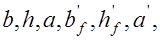 площадь сечения арматуры
площадь сечения арматуры 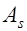 , возможно и
, возможно и 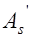 , класс бетона и арматуры, изгибающий момент от расчетных нагрузок
, класс бетона и арматуры, изгибающий момент от расчетных нагрузок 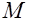 . Требуется проверить прочность сечения; б) известны размеры сечения
. Требуется проверить прочность сечения; б) известны размеры сечения 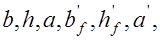 класс бетона и арматуры, изгибающий момент от расчетных нагрузок
класс бетона и арматуры, изгибающий момент от расчетных нагрузок 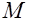 . Требуется определить площадь сечения арматуры
. Требуется определить площадь сечения арматуры 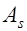 , возможно и
, возможно и 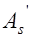 .
.
Порядок решения задач приведен в блок-схемах 14.1 и 14.2. Здесь при решении задач первого типа задач принято двойное армирование. При одиночном армировании исчезнут члены, содержащие 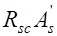 .
.
14.2. РАСЧЕТ НОРМАЛЬНЫХ СЕЧЕНИЙ ИЗГИБАЕМЫХ
ЭЛЕМЕНТОВ С ЖЕСТКОЙ АРМАТУРОЙ
Экспериментально установлено, что совместная работа жесткой арматуры с бетоном сохраняется вплоть до разрушения элементов. В период разрушения несущая способность жесткой арматуры и бетона сжатой зоны используется полностью. При этом несущая способность элементов не зависит от начальных напряжений в арматуре, приобретенных ею в процессе возведения конструкции. В балках, армированных низкими профилями (14.1) для связи бетона сжатой зоны сечения с жесткой арматурой к последней привариваются специальные анкерные стержни. При отсутствии связи бетона сжатой зоны с жесткой арматурой элемент разрушения от среза бетона сдвигающими силами по плоскости контакта с арматурой. В элементах, армированных высокими профилями, совместность работы обеспечивается и при отсутствии хомутов, так как сплошная металлическая стенка полностью воспринимает поперечную силу. До бетонирования элементов жесткую арматуру рассчитывают по нормам для стальных конструкций на воздействие нагрузок, возникающих в процессе возведения здания.
При расчете сечений изгибаемых элементов с жесткой арматурой различают три случая в зависимости от положения нейтральной оси: а) нейтральная ось не пересекает профиль жесткой арматуры; б) нейтральная ось пересекает стенку профиля жесткой арматуры; в) нейтральная ось пересекает полку профиля жесткой арматуры. Условия прочности для изгибаемых элементов с жесткой арматурой можно получить из статических условий для моментов и усилий. При этом эпюры напряжений в бетоне сжатой зоны и в жесткой арматуре принимаются прямоугольными. Рассмотрим расчет прямоугольных сечений.
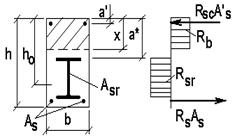
Случай 1. Высоту сжатой зоны определяют из статического условия в проекциях усилий на продольную ось (рис. 14.1):
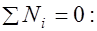
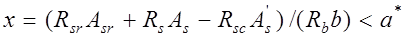 , (14.1) где
, (14.1) где 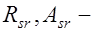 расчетное сопротивление и площадь сечения жесткой арматуры.
расчетное сопротивление и площадь сечения жесткой арматуры.
Если при этом 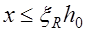 , то прочность сечения проверяют из статического условия моментов относительно центра тяжести сечения растянутой арматуры с учетом жесткой арматуры
, то прочность сечения проверяют из статического условия моментов относительно центра тяжести сечения растянутой арматуры с учетом жесткой арматуры
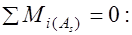
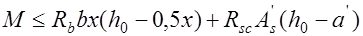 . (14.2)
. (14.2)
Если 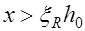 , то в соотношении (14.2) необходимо заменить
, то в соотношении (14.2) необходимо заменить 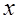 на
на 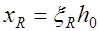 . Следует заметить, что при определении
. Следует заметить, что при определении 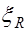 вместо
вместо 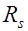 необходимо ввести осредненную характеристику
необходимо ввести осредненную характеристику
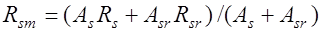 .
.
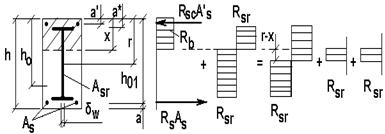
Случай 2. (рис. 14.2). Высоту сжатой зоны по-прежнему определяют из условия равновесия в проекциях на продольную ось
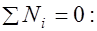
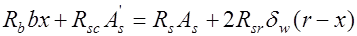 , (14.2) откуда
, (14.2) откуда 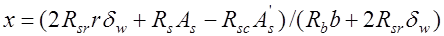 , (14.3) где
, (14.3) где 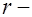 расстояние от крайнего сжатого волокна сечения до центра тяжести жесткой арматуры;
расстояние от крайнего сжатого волокна сечения до центра тяжести жесткой арматуры; 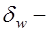 толщина стенки жесткой арматуры.
толщина стенки жесткой арматуры.
В этом случае условие прочности получают из статического уравнения моментов относительно нейтральной оси:
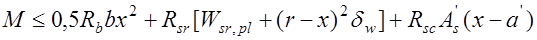 +
+
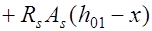 , (14.4) где
, (14.4) где 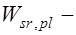 пластический момент сопротивления жесткой арматуры относительно оси, делящей сечение на две равные площади, для двутавров и швеллеров
пластический момент сопротивления жесткой арматуры относительно оси, делящей сечение на две равные площади, для двутавров и швеллеров 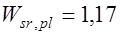
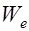 ,
, 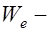 упругий момент сопротивления жесткой арматуры по сортаменту;
упругий момент сопротивления жесткой арматуры по сортаменту; 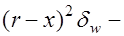 поправка к величине
поправка к величине 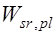 равная пластическому моменту сопротивления части стенки между нейтральной и центральной осями профиля арматуры.
равная пластическому моменту сопротивления части стенки между нейтральной и центральной осями профиля арматуры.
Случай 3. (рис. 14.3). Если при определении высоты сжатой зоны 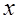 из соотношения (14.1) оказывается, что нейтральная ось пересекает стенку жесткой арматуры, а при определении
из соотношения (14.1) оказывается, что нейтральная ось пересекает стенку жесткой арматуры, а при определении 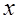 из уравнения (14.3) – не пересекает, то нейтральная ось фактически проходит в пределах толщины верхней полки профиля. Тогда эту полку не учитывают в расчетах. Прочность сечения проверяют из статического уравнения моментов относительно нейтральной оси:
из уравнения (14.3) – не пересекает, то нейтральная ось фактически проходит в пределах толщины верхней полки профиля. Тогда эту полку не учитывают в расчетах. Прочность сечения проверяют из статического уравнения моментов относительно нейтральной оси:
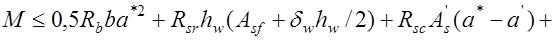
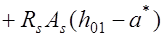 , (14.5)
, (14.5)
где 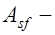 площадь сечения растянутой полки профиля;
площадь сечения растянутой полки профиля; 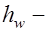 высота стенки.
высота стенки.
При этом если окажется, что 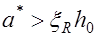 , то прочность проверяют при
, то прочность проверяют при 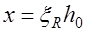 и соотношения (14.2).
и соотношения (14.2).
 | |||
 | |||
Прочность нормальных сечений тавровых элементов проверяют в зависимости от положения нейтральной оси: а) если она проходит в полке сечения, то расчет ведут по формулам (14.1) – (14.5), как для прямоугольных сечений шириной
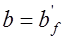 ; б) если нейтральная ось проходит в ребре, то расчет ведут с учетом свесов полок сечения по аналогии с прямоугольными сечениями.
; б) если нейтральная ось проходит в ребре, то расчет ведут с учетом свесов полок сечения по аналогии с прямоугольными сечениями.
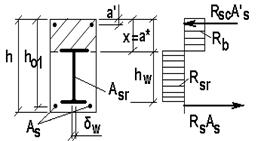 |
Рис. 14.1 Рис. 14.2
Рис. 14.3
|


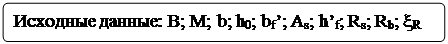
 |
НЕТ


|
 | |||||
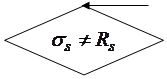 |  | ||||

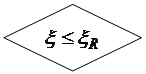
 НЕТ
НЕТ



|

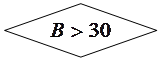



 ДА ДА НЕТ
ДА ДА НЕТ

|
ДА
|
|


 ДА НЕТ
ДА НЕТ

|

 Блок-схема 13.3
Блок-схема 13.3

| |||
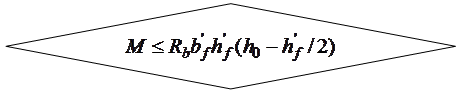 | |||
ДА
 |
|


|
|
 ДА НЕТ НЕТ
ДА НЕТ НЕТ
 | |||||
 | |||||
 | |||||
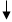
 ДА
ДА
 |
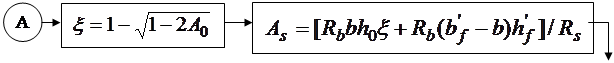


|
|
 | |||||
 | |||||
 | |||||
 ДА
ДА
|

|
 НЕТ
НЕТ
 |
|

Дата добавления: 2018-09-24; просмотров: 862;