НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ НАКЛОННЫХ СЕЧЕНИЙ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ
В изгибаемых элементах от действия внешних нагрузок вблизи опор возникают моменты и поперечные силы. От их совместного действия в наклонных сечениях элемента возникают главные растягивающие 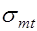 и главные сжимающие
и главные сжимающие 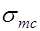 напряжения (рис. 17.1)
напряжения (рис. 17.1)
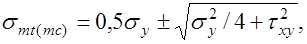 (17.1) где
(17.1) где 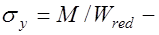 нормальные напряжения вдоль оси
нормальные напряжения вдоль оси 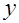 от действия момента;
от действия момента; 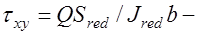 касательные напряжения;
касательные напряжения; 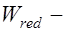 момент сопротивления приведенного сечения;
момент сопротивления приведенного сечения; 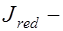 момент инерции сечения;
момент инерции сечения; 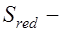 статический момент отсеченной площади сечения.
статический момент отсеченной площади сечения.
У нейтральной оси сечения, где 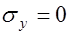 , главные напряжения таковы
, главные напряжения таковы 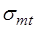
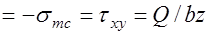 ,
, 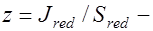 плечо внутренней пары.
плечо внутренней пары.
Если внешняя нагрузка будет такова, что 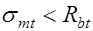 , то элемент будет работать без наклонных трещин (стадия работы без трещин). Если же нагрузка возрастает и
, то элемент будет работать без наклонных трещин (стадия работы без трещин). Если же нагрузка возрастает и 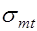 приблизятся к
приблизятся к 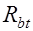 , то будут образовываться наклонные трещины. Тогда в пределах трещины растягивающие напряжения будут восприниматься поперечной и продольной арматурой и отгибами. При этом в работе участвует сжатая зона бетона над трещиной. С повышением нагрузки возможно разрушение элемента по наклонному сечению. Разрушение может произойти по одной из схем: а) от действия изгибающего момента обе части элемента, образовавшиеся после появления наклонной трещины, поворачиваются относительно центра тяжести сжатой зоны бетона над наклонной трещиной. Трещина раскрывается и развивается по высоте, а сжатая зона уменьшается. Когда напряжения во всей арматуре, пересекаемой трещиной достигнут предельных значений
, то будут образовываться наклонные трещины. Тогда в пределах трещины растягивающие напряжения будут восприниматься поперечной и продольной арматурой и отгибами. При этом в работе участвует сжатая зона бетона над трещиной. С повышением нагрузки возможно разрушение элемента по наклонному сечению. Разрушение может произойти по одной из схем: а) от действия изгибающего момента обе части элемента, образовавшиеся после появления наклонной трещины, поворачиваются относительно центра тяжести сжатой зоны бетона над наклонной трещиной. Трещина раскрывается и развивается по высоте, а сжатая зона уменьшается. Когда напряжения во всей арматуре, пересекаемой трещиной достигнут предельных значений 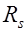 , произойдет разрыв арматуры и разрушение сжатой зоны бетона (рис. 17.2). Разрушение происходит, как и по нормальному сечению от действия момента. Элемент может разрушиться и в том случае, когда напряжения в арматуре меньше
, произойдет разрыв арматуры и разрушение сжатой зоны бетона (рис. 17.2). Разрушение происходит, как и по нормальному сечению от действия момента. Элемент может разрушиться и в том случае, когда напряжения в арматуре меньше 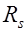 , но недостаточна ее анкеровка, что приводит к проскальзыванию арматуры; б) когда сечение арматуры достаточно велико и обеспечена надежность анкеровки, что препятствует повороту обеих частей элемента, разрушение происходит после достижения предельных напряжений и в предельных напряжений в поперечной и наклонной арматуре, пересекающей трещину из-за среза бетона сжатой зоны над наклонной трещиной (рис. 17.3). Обе части элемента при этом смещаются друг против друга. Такой характер разрушения вызывается действием поперечной силы; в) при малой ширине сечения элемента
, но недостаточна ее анкеровка, что приводит к проскальзыванию арматуры; б) когда сечение арматуры достаточно велико и обеспечена надежность анкеровки, что препятствует повороту обеих частей элемента, разрушение происходит после достижения предельных напряжений и в предельных напряжений в поперечной и наклонной арматуре, пересекающей трещину из-за среза бетона сжатой зоны над наклонной трещиной (рис. 17.3). Обе части элемента при этом смещаются друг против друга. Такой характер разрушения вызывается действием поперечной силы; в) при малой ширине сечения элемента 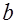 состояние разрушения может быть достигнуто не только при повороте частей элемента и смещения их друг относительно друга, но и из-за раздробления бетона стенки между наклонными трещинами от главных сжимающих напряжений
состояние разрушения может быть достигнуто не только при повороте частей элемента и смещения их друг относительно друга, но и из-за раздробления бетона стенки между наклонными трещинами от главных сжимающих напряжений 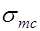 , когда они приблизятся к расчетному сопротивлению бетона на сжатие
, когда они приблизятся к расчетному сопротивлению бетона на сжатие 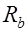 (рис. 17.4).
(рис. 17.4).
Для обеспечения прочности наклонных сечений изгибаемых элементов должен быть произведен расчет на сжатие в полосе бетона стенки балки между наклонными трещинами, расчет по наклонной трещине на действие изгибающего момента, расчет по наклонной трещине на действие поперечной силы.
17.2. РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ
НАКЛОННЫХ СЕЧЕНИЙ НА ДЕЙСТВИЕ НАКЛОННЫХ
СЖИМАЮЩИХ НАПРЯЖЕНИЙ
Разрушение изгибаемых элементов по сжатой полосе в стенке балки между наклонными трещинами возможно в тонкостенных железобетонных элементах, когда от совместного действия предварительного обжатия и внешних нагрузок в стенке возникают значительные сжимающие усилия. Так как в стенке одновременно возникают и главные растягивающие напряжения, то есть стенка находится в двухосном напряженном состоянии, то в момент разрушения главные сжимающие напряжения в стенках значительно меньше прочности бетона при осевом сжатии 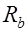 .
.
Экспериментально установлено, что прочность стенки на сжатие будет обеспечена, если удовлетворяется условие:
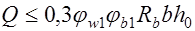 , (17.2)
, (17.2)
где 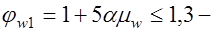 коэффициент, учитывающий влияние поперечной арматуры;
коэффициент, учитывающий влияние поперечной арматуры; 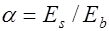 ;
; 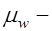 коэффициент поперечного армирования,
коэффициент поперечного армирования, 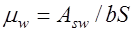 ,
, 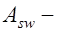 соответственно площадь сечения поперечной арматуры, расположенной в одной нормальной к оси элемента плоскости,
соответственно площадь сечения поперечной арматуры, расположенной в одной нормальной к оси элемента плоскости, 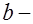 толщина стенки таврового или двутаврового сечения, либо ширина прямоугольного сечения,
толщина стенки таврового или двутаврового сечения, либо ширина прямоугольного сечения, 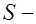 шаг поперечных стержней по нормали к ним (рис. 17.5);
шаг поперечных стержней по нормали к ним (рис. 17.5); 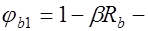 коэффициент, учитывающий влияние прочности бетона,
коэффициент, учитывающий влияние прочности бетона, 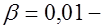 для тяжелого бетона,
для тяжелого бетона, 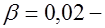 для легкого.
для легкого.
Если условие (17.2) не выполняется, то следует увеличить сечение элемента, либо повысить класс бетона.
17.3. РАСЧЕТ ПРОЧНОСТИ ПО НАКЛОННОЙ ТРЕЩИНЕ НА
ДЕЙСТВИЕ ПОПЕРЕЧНОЙ СИЛЫ
Наклонные трещины в элементах образовываться не будут если
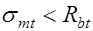 . Для железобетонных конструкций этому условию соответствует приближенная экспериментальная зависимость
. Для железобетонных конструкций этому условию соответствует приближенная экспериментальная зависимость
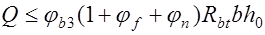 , (17.3) где
, (17.3) где 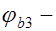 эмпирический коэффициент, принимаемый для тяжелого бетона равным 0,6;
эмпирический коэффициент, принимаемый для тяжелого бетона равным 0,6; 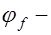 коэффициент, учитывающий влияние сжатых полок:
коэффициент, учитывающий влияние сжатых полок:
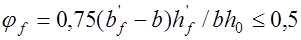 , (17.4) при этом принимается
, (17.4) при этом принимается 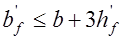 ;
; 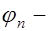 коэффициент, учитывающий влияние продольных сил от нагрузки и предварительного обжатия бетона:
коэффициент, учитывающий влияние продольных сил от нагрузки и предварительного обжатия бетона:
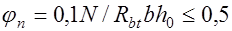 - (17.5)
- (17.5)
- при наличии продольных сжимающих усилий от внешней нагрузки и предварительного обжатия бетона в растянутой зоне элемента, либо
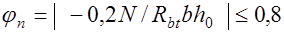 - (17.6) - при наличии продольных растягивающих усилий от внешней нагрузки.
- (17.6) - при наличии продольных растягивающих усилий от внешней нагрузки.
В любом случае в формуле (17.3) принимается 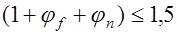 .
.
Таким образом, при соблюдении условия (17.3) расчет наклонных сечений по поперечной силе не требуется, а арматура может быть установлена по конструктивным соображениям. Если же условие (17.3) не выполняется, то прочность сечения можно обеспечить путем постановки поперечной, а иногда и наклонной арматуры в соответствии с расчетом.
Для получения расчетных условий рассмотрим наклонное сечение в предельном состоянии (рис. 17.5). Для обеспечения прочности наклонного сечения необходимо чтобы расчетная поперечная сила от внешней нагрузки 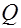 не превышала суммы проекций расчетных усилий в поперечной арматуре, отогнутых стержней и в бетоне сжатой зоны на вертикальную ось:
не превышала суммы проекций расчетных усилий в поперечной арматуре, отогнутых стержней и в бетоне сжатой зоны на вертикальную ось:
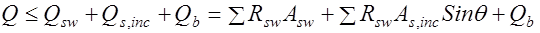 , (17.7) где
, (17.7) где 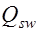 и
и 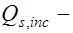 поперечные силы, воспринимаемые хомутами и отгибами, пересекающими наклонное сечение;
поперечные силы, воспринимаемые хомутами и отгибами, пересекающими наклонное сечение; 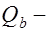 поперечная сила, воспринимаемая бетоном сжатой зоны;
поперечная сила, воспринимаемая бетоном сжатой зоны; 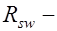 расчетное сопротивление хомутов и отгибов при расчете на поперечную силу;
расчетное сопротивление хомутов и отгибов при расчете на поперечную силу; 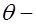 угол наклона отгибов к горизонтали.
угол наклона отгибов к горизонтали.
В общем случае поперечная сила 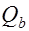 определяется по эмпирической зависимости:
определяется по эмпирической зависимости:
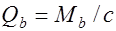 , (17.8) где
, (17.8) где 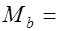
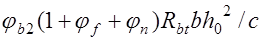 , (17.9) где
, (17.9) где 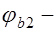 эмпирический коэффициент, принимаемый для тяжелого бетона равным 2;
эмпирический коэффициент, принимаемый для тяжелого бетона равным 2; 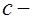 длина горизонтальной проекции наклонного сечения, представляющая собой расстояние от вершины наклонной трещины до опоры (рис. 17.5).
длина горизонтальной проекции наклонного сечения, представляющая собой расстояние от вершины наклонной трещины до опоры (рис. 17.5).
При этом величина 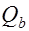 должна приниматься не менее
должна приниматься не менее 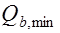 , вычисляемого по формуле (17.3).
, вычисляемого по формуле (17.3).
Величину 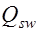 можно также определить из выражения
можно также определить из выражения
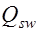
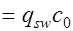 , (17.10) где
, (17.10) где 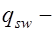 погонное усилие в поперечных стержнях, отнесенное к единице длины элемента и представляемое формулой
погонное усилие в поперечных стержнях, отнесенное к единице длины элемента и представляемое формулой
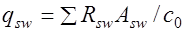 ; (17.11)
; (17.11) 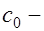 длина проекции опасной наклонной трещины на продольную ось элемента, на которой учитывается работа хомутов и определяемая из минимума выражения
длина проекции опасной наклонной трещины на продольную ось элемента, на которой учитывается работа хомутов и определяемая из минимума выражения 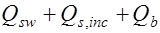 .
.
В выражениях (17.10) и (17.11) 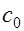 должно приниматься не более
должно приниматься не более 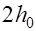 и не более
и не более 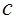 , а также не менее
, а также не менее 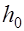 , если
, если 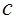 >
> 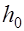 .
.
В элементах без поперечной и наклонной арматуры с целью ограничения развития трещин должно соблюдаться условие
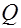
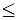
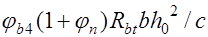 , (17.12) где правая часть этого условия принимается не более
, (17.12) где правая часть этого условия принимается не более 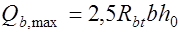 и не менее
и не менее 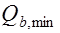 ;
; 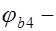 эмпирический коэффициент, принимаемый для тяжелого бетона равный 1,5.
эмпирический коэффициент, принимаемый для тяжелого бетона равный 1,5.
Значение проекции 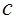 в выражении (17.12) принимается не более
в выражении (17.12) принимается не более 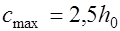 .
.
При равномерно распределенной нагрузке, если выполняется условие
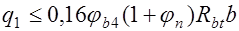 , (17.13) принимают
, (17.13) принимают 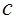
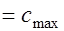 , при невыполнении этого условия принимают
, при невыполнении этого условия принимают
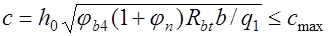 . (17.14) Здесь
. (17.14) Здесь 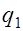 - заменяющая погонная нагрузка, которая при фактически равномерно распределенной нагрузке
- заменяющая погонная нагрузка, которая при фактически равномерно распределенной нагрузке 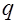 принимается равной интенсивности этой нагрузке, а при нагрузке, приводящейся к равномерной по эквивалентной огибающей эпюре моментов принимают
принимается равной интенсивности этой нагрузке, а при нагрузке, приводящейся к равномерной по эквивалентной огибающей эпюре моментов принимают
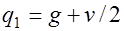 ,
,
где 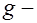 интенсивность постоянной нагрузки;
интенсивность постоянной нагрузки; 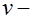 интенсивность временной нагрузки.
интенсивность временной нагрузки.
 |
Рис. 17.1 Рис. 17.2 Рис. 17.3 Рис. 17.4
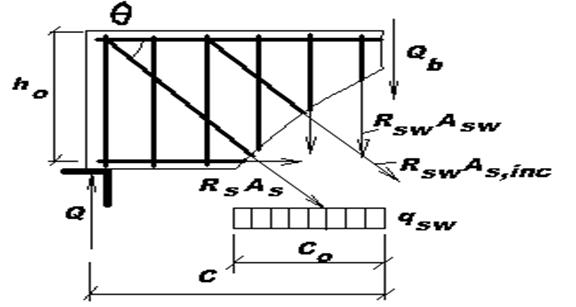 |
Рис. 17.5
Дата добавления: 2018-09-24; просмотров: 596;
