ОБЩИЕ ПРИНЦИПЫ РАСЧЕТА ПОПЕРЕЧНЫХ И НАКЛОННЫХ СТЕРЖНЕЙ

Рассмотрим изгибаемый элемент, армированный продольной и поперечной арматурой без отгибов 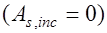. В этом случае условие прочности по поперечной силе (17.3) будет иметь вид 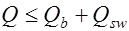. При известной величине проекции 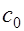усилие 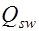можно выразить через погонную силу, воспринимаемую поперечными стержнями 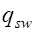, которую можно определить следующим образом (рис. 18.1)

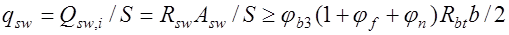, (18.1) где 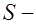шаг поперечных стержней по длине элемента.

Тогда, учитывая 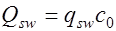, получим:

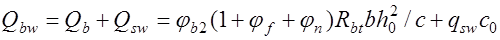. (18.2)

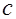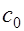Условие (18.2) справедливо для произвольных значений и . При увеличени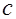и и 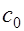значение 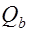уменьшается, а значение 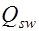наоборот – увеличивается. Необходимо подобрать такое наклонное сечение, в котором несущая способность наименьшая. Для такого расчетного сечения элемента армированного без наклонных стержней, принимают значение

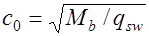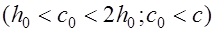, . (18.3)

Наименьшую несущую способность наклонного сечения, очевидно, можно определить из условия (полагая, что ):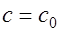

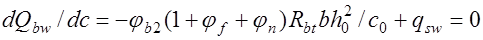. (18.4)

Из этого выражения (18.4) и вытекает зависимости (18.3). Подставив 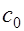из (18.3) в выражение (18.2) получим несущую способность наклонного сечения по поперечной силе

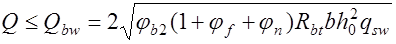. (18.5)

Шаг поперечных стержней 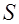должен быть ограничен исходя из условия прочности бетона по наклонному сечению между двумя соседними хомутами

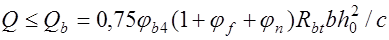. (18.6)

Заменив здесь 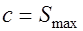, получим

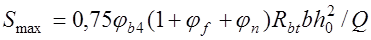, (18.7) где 0,75 – коэффициент, учитывающий возможные смещения поперечной арматуры.

При расчете элементов на действие равномерно распределенной нагрузки 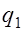принимают

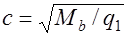. (18.8)