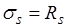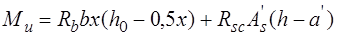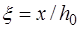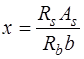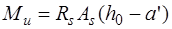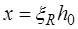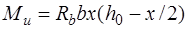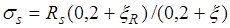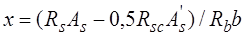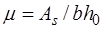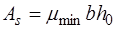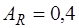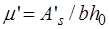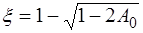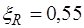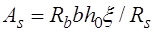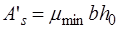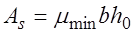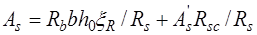РАСЧЕТ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ НОРМАЛЬНОГО СЕЧЕНИЯ ПРЯМОУГОЛЬНОЙ ФОРМЫ С ДВОЙНОЙ НЕНАПРЯГАЕМОЙ АРМАТУРОЙ. ТИПЫ ЗАДАЧ
В сечениях с двойной арматурой кроме арматуры площадью 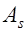 устанавливается расчетная арматура площадью
устанавливается расчетная арматура площадью 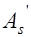 в сжатой зоне. Такие сечения характеризуются повышенным расходом стали и поэтому их применение должно быть экономически оправданным. Сечения с двойной арматурой применяются когда прочность бетона сжатой зоны сечения с одиночным армированием при заданном классе бетона мала, то есть
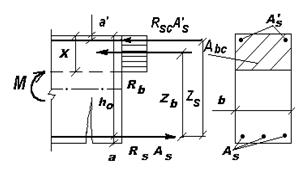
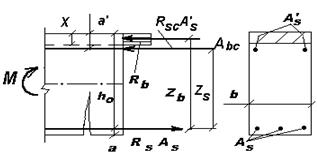
в сжатой зоне. Такие сечения характеризуются повышенным расходом стали и поэтому их применение должно быть экономически оправданным. Сечения с двойной арматурой применяются когда прочность бетона сжатой зоны сечения с одиночным армированием при заданном классе бетона мала, то есть 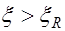 , а размеры сечения нельзя увеличить из-за ограничения габаритов элемента по тем или иным причинам. Рассмотрим расчетное сечение в предельном состоянии (рис. 13.1). Записывая уравнение равновесия всех действующих в сечении внутренних усилий в проекциях на продольную горизонтальную ось:
, а размеры сечения нельзя увеличить из-за ограничения габаритов элемента по тем или иным причинам. Рассмотрим расчетное сечение в предельном состоянии (рис. 13.1). Записывая уравнение равновесия всех действующих в сечении внутренних усилий в проекциях на продольную горизонтальную ось: 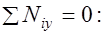
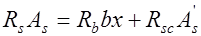 , или
, или 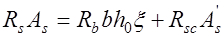 (13.1)
(13.1)
и определяя моменты относительно горизонтальной оси перпендикулярной плоскости изгиба, проходящей через центр тяжести растянутой арматуры, получим условие прочности
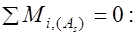
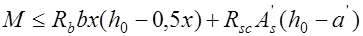 , (13.2)
, (13.2)
или 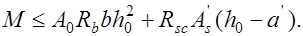 (13.3)
(13.3)
Соотношения (13.1) – (13.3) справедливы в тех случаях, когда арматура площадью 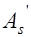 расположена в сжатой зоне бетона, если же эта арматура находится вблизи нейтральной оси, то она совсем не принимает участия в работе сжатой зоны или принимает частичное участие. Таким образом, выражения (13.1) – (13.3) справедливы при
расположена в сжатой зоне бетона, если же эта арматура находится вблизи нейтральной оси, то она совсем не принимает участия в работе сжатой зоны или принимает частичное участие. Таким образом, выражения (13.1) – (13.3) справедливы при 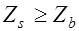 , то есть
, то есть 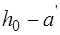
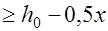 , или
, или 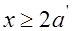 . Тогда если из уравнения (13.1) получим
. Тогда если из уравнения (13.1) получим 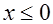 , что возможно при
, что возможно при 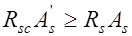 , то прочность проверяется без учета работы бетона сжатой зоны исходя из уравнения равновесия в виде моментов, вычисленных относительно оси, проходящей через центр тяжести сечения арматуры сечением
, то прочность проверяется без учета работы бетона сжатой зоны исходя из уравнения равновесия в виде моментов, вычисленных относительно оси, проходящей через центр тяжести сечения арматуры сечением 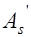 :
:
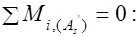
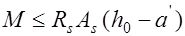 , (13.4)
, (13.4)
либо без учета арматуры сечением 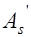 как для сечения с одиночным армированием.
как для сечения с одиночным армированием.
Для выяснения случая расчета необходимо установить степень участия сжатой арматуры в работе сечения. Если высота сжатой зоны, вычисленная с учетом только половины площади сечения сжатой арматуры:
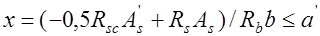 , (13.5) то расчет прочности проводится без учета сжатой арматуры, так как в этом случае
, (13.5) то расчет прочности проводится без учета сжатой арматуры, так как в этом случае 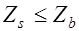 и несущая способность выше, чем при расчете из условия (13.4).
и несущая способность выше, чем при расчете из условия (13.4).
Соотношения (13.2), (13.3) справедливы при высоте сжатой зоны бетона 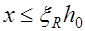 , которая определяется из условия (13.1). В противном случае для элементов из бетона класса В30 и ниже при наличии арматуры классов А-I, А-II, А-III, Вр-I разрешается заменять
, которая определяется из условия (13.1). В противном случае для элементов из бетона класса В30 и ниже при наличии арматуры классов А-I, А-II, А-III, Вр-I разрешается заменять 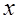 на
на 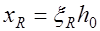 . При наличие другой арматуры или при более высоких классах бетона при
. При наличие другой арматуры или при более высоких классах бетона при 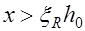 , установленной из уравнения (13.1), расчет следует выполнять по формулам (13.2), (13.3), в которых высоту сжатой зоны необходимо принимать из выражения:
, установленной из уравнения (13.1), расчет следует выполнять по формулам (13.2), (13.3), в которых высоту сжатой зоны необходимо принимать из выражения:
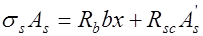 , (13.6)
, (13.6)
где 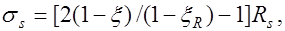 или как это рекомендовано в последней редакции СНиП2.03.01-84* эти напряжения можно определять по эмпирической зависимости
или как это рекомендовано в последней редакции СНиП2.03.01-84* эти напряжения можно определять по эмпирической зависимости 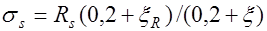 .
.
При расчете сечений возможны три типа задач: а) известны размеры сечения 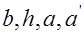 и площадь сечения арматуры
и площадь сечения арматуры 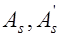 , класс бетона, класс арматуры, изгибающий момент от расчетных нагрузок
, класс бетона, класс арматуры, изгибающий момент от расчетных нагрузок 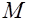 . Требуется проверить прочность сечения; б) известны размеры сечения, площадь сечения арматуры
. Требуется проверить прочность сечения; б) известны размеры сечения, площадь сечения арматуры 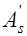 , класс бетона, класс арматуры, изгибающий момент от расчетных нагрузок
, класс бетона, класс арматуры, изгибающий момент от расчетных нагрузок 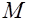 . Требуется определить
. Требуется определить 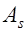 ; в) известны размеры сечения, класс бетона, класс арматуры, изгибающий момент от расчетных нагрузок
; в) известны размеры сечения, класс бетона, класс арматуры, изгибающий момент от расчетных нагрузок 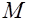 . Требуется определить
. Требуется определить 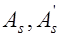 .
.
 |  | ||
Решение этих задач выполняется по блок-схемам 13.1 – 13.3.
Рис. 13.1
13.2. РАСЧЕТ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ НОРМАЛЬНОГОСЕЧЕНИЯ ТАВРОВОЙ И ДВУТАВРОВОЙ ФОРМЫ С НЕНАПРЯГАЕМЫМ АРМИРОВАНИЕМ
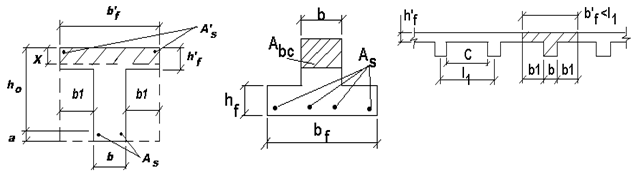
Тавровые сечения часто встречаются в практике проектирования как в отдельных железобетонных элементах – балках (рис. 13.2, 13.3), так и в составе конструкций монолитных и сборных ребристых перекрытий (рис. 13.4). Тавровые сечения состоят из полки и ребра. Чаще применяются элементы с полкой, расположенной в сжатой зоне. Такой профиль по сравнению с прямоугольным сечением шириной, равной ширине полки, имеет практически одинаковую несущую способность, но значительно меньший расход бетона из-за меньших размеров сечения в растянутой зоне. Тавровые сечения с полкой в растянутой зоне, применяются реже, так как в этом случае полка не повышает несущую способность элемента. Такие сечения рассчитывают как прямоугольные шириной равной ширине ребра. На рис. 13.2 – 13.4 приняты следующие обозначения: 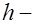 полная высота сечения;
полная высота сечения; 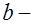 ширина ребра;
ширина ребра; 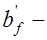 ширина сжатой полки;
ширина сжатой полки; 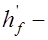 высота сжатой полки;
высота сжатой полки; 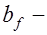 ширина растянутой полки;
ширина растянутой полки; 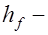 высота растянутой полки.
высота растянутой полки.
Тавровое сечение имеет, как правило, одиночное армирование. При большой ширине полок участки свесов более удаленные от ребра напряжены меньше. Поэтому ширина свесов полки в каждую сторону от ребра, вводимая в расчет ограничивается. Для отдельных балок при консольных свесах полок ширина полки 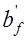 принимается:
принимается: 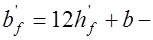 при
при 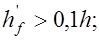
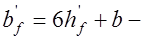 при
при 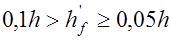 ;
; 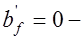 при
при 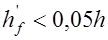 . В расчете ребристых монолитных и сборных плит ширина свесов принимается не более половины расстояния в свету между ребрами и не более 1/6 длины рассчитываемого элемента, то есть
. В расчете ребристых монолитных и сборных плит ширина свесов принимается не более половины расстояния в свету между ребрами и не более 1/6 длины рассчитываемого элемента, то есть 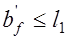 и
и 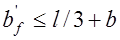 . Если толщина полки при этом
. Если толщина полки при этом 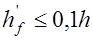 и отсутствуют поперечные ребра или их шаг больше чем расстояние между продольными ребрами, то
и отсутствуют поперечные ребра или их шаг больше чем расстояние между продольными ребрами, то 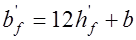 .
.
При расчете тавровых сечений с полкой в сжатой зоне различают два расчетных случая в зависимости от положения нижней границы сжатой зоны: а) эта граница проходит в пределах полки 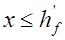 (рис. 13.2, 13.5); б) эта граница проходит ниже полки в ребре
(рис. 13.2, 13.5); б) эта граница проходит ниже полки в ребре 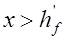 (рис. 13.6). Рассмотрим предельный случай, когда нижняя граница сжатой зоны проходит по нижней грани полки, то есть когда
(рис. 13.6). Рассмотрим предельный случай, когда нижняя граница сжатой зоны проходит по нижней грани полки, то есть когда 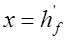 . В этом случае условия прочности нормального сечения запишутся так (рис. 13.5):
. В этом случае условия прочности нормального сечения запишутся так (рис. 13.5):
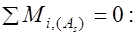
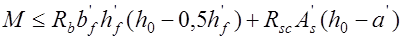 ; (13.7)
; (13.7)
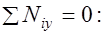
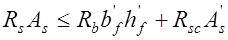 . (13.8)
. (13.8)
Соотношения (13.7), (13.8) используется для определения положения нейтральной оси. При определении прочности сечения нейтральная ось проходит в полке, если усилие в растянутой арматуре меньше или равно усилию, которое воспринимается полностью сжатой полкой, то есть при 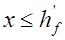 условие (13.8) выполняется. В противном случае нейтральная ось пересекает ребро, то есть при
условие (13.8) выполняется. В противном случае нейтральная ось пересекает ребро, то есть при 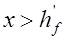 условие (13.8) не выполняется. Соотношением (13.7) пользуются для определения положения нейтральной оси при расчете площади поперечного сечения арматуры
условие (13.8) не выполняется. Соотношением (13.7) пользуются для определения положения нейтральной оси при расчете площади поперечного сечения арматуры 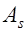 . При этом если условие (13.7) выполняется, то нейтральная ось проходит в полке, а в противном случае она пересекает ребро.
. При этом если условие (13.7) выполняется, то нейтральная ось проходит в полке, а в противном случае она пересекает ребро.
Получим расчетные условия прочности для случая, когда нейтральная ось проходит в полке 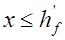 и когда – в ребре
и когда – в ребре 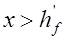 .
.
Случай 1: 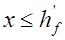 . Так как нейтральная ось не пересекает ребро, то расчет ведется как для прямоугольного сечения при замене в расчетных формулах величины
. Так как нейтральная ось не пересекает ребро, то расчет ведется как для прямоугольного сечения при замене в расчетных формулах величины 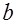 на
на 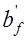 , то есть:
, то есть:
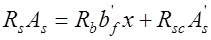 ;
; 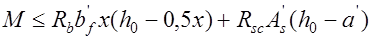 (13.9)
(13.9)
или
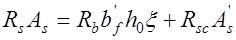 ;
; 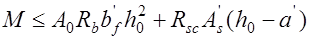 . (13.9’)
. (13.9’)
Случай 2: 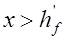 . В этом случае сжатая зона состоит из сжатых свесов
. В этом случае сжатая зона состоит из сжатых свесов
и сжатой зоны ребра. Тогда имеем:
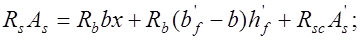 (13.10)
(13.10)
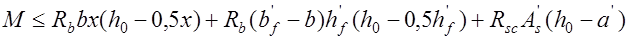 ,
,
или 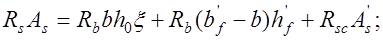 (13.10’)
(13.10’)
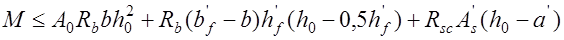 .
.
 |
Расчетные соотношения (13.10) получены в предположении, что
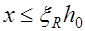 . Если же
. Если же 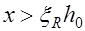 , то для расчета сечений используются те же методы и допущения, что и при расчете прямоугольных сечений.
, то для расчета сечений используются те же методы и допущения, что и при расчете прямоугольных сечений.
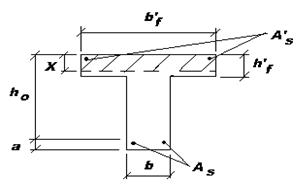 | 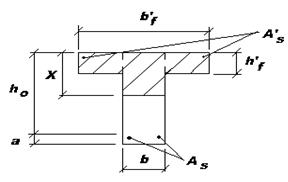 | ||
Рис. 13.2 Рис. 13.3 Рис. 13.4
Рис. 13.5 Рис. 13.6
|

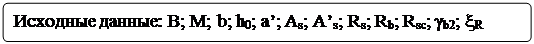
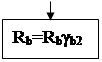 | |||||
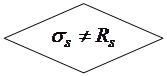 | 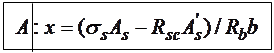 | ||||
 НЕТ
НЕТ


|
 ДА
ДА
|

 ДА
ДА


|




 ДА
ДА
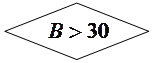
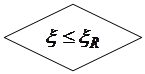 НЕТ НЕТ ДА
НЕТ НЕТ ДА
 | |||||||
 | |||||||
 | |||||||
 | |||||||
|
 НЕТ
НЕТ

|
 ДА НЕТ
ДА НЕТ
|
|

 | |||
 | |||


|

 НЕТ
НЕТ

|
 ДА
ДА
 | |||
| |||


Блок-схема 13.2


|

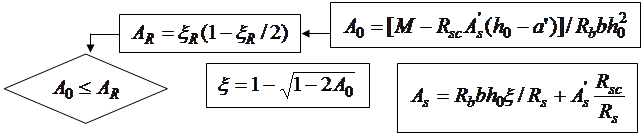

 ДА
ДА
 |
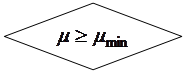
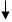
|
|


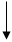

 ДА
ДА




|
НЕТ
Блок-схема 13.3


|

 |


 ДА НЕТ ДА
ДА НЕТ ДА
| |||
 | |||

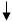
|

|
|
|

|

|
 НЕТ
НЕТ
 | |||
 | |||






|

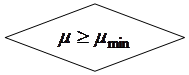
|
 ДА
ДА
НЕТ ДА
Дата добавления: 2018-09-24; просмотров: 2168;