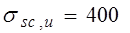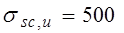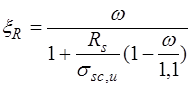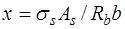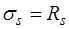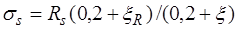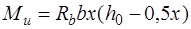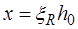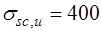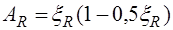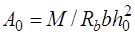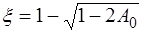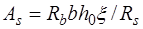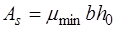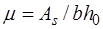ОБЩИЙ СЛУЧАЙ РАСЧЕТА ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ЛЮБОГО СИММЕТРИЧНОГО ПРОФИЛЯ ПО ПРОЧНОСТИ НОРМАЛЬНОГО СЕЧЕНИЯ
Прочность изгибаемых элементов по нормальным сечениям рассчитывают по стадии разрушения (12.1). В расчетной схеме усилий принимается, что на элемент действует изгибающий момент М, вычисляемый при расчетных значениях нагрузок. При построении условий прочности нормальных сечений в стадии разрушения принимаются следующие допущения: а) криволинейная эпюра напряжений в бетоне сжатой зоны заменяется прямоугольной интенсивностью равной 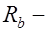 расчетному сопротивлению сжатию; б) работой растянутой зоны бетона между трещинами пренебрегают; в) продольная ненапрягаемая арматура площадью сечения
расчетному сопротивлению сжатию; б) работой растянутой зоны бетона между трещинами пренебрегают; в) продольная ненапрягаемая арматура площадью сечения 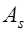 испытывает напряжения
испытывает напряжения 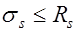 , а напрягаемая площадью
, а напрягаемая площадью 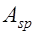 -
- 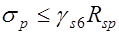 ; г) продольная ненапрягаемая арматура в сжатой зоне площадью
; г) продольная ненапрягаемая арматура в сжатой зоне площадью 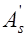 испытывает напряжения равные
испытывает напряжения равные 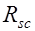 , а напрягаемая площадью
, а напрягаемая площадью 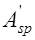 - напряжения
- напряжения 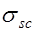 ; д) сечение элемента любой формы симметрично относительно оси, совпадающей с силовой плоскостью изгиба.
; д) сечение элемента любой формы симметрично относительно оси, совпадающей с силовой плоскостью изгиба.
Железобетонные изгибаемые элементы рекомендуется проектировать так, чтобы высота сжатой зоны бетона 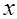 удовлетворяла условию
удовлетворяла условию 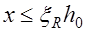 , так как при
, так как при 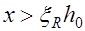 прочность растянутой арматуры используется не полностью, что экономически не целесообразно.
прочность растянутой арматуры используется не полностью, что экономически не целесообразно.
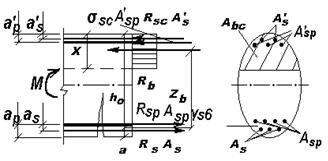
Рассмотрим нормальное сечение в предельном состоянии (рис. 12.1). Предположим, что 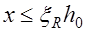 . На рис. 12.1 введены следующие обозначения:
. На рис. 12.1 введены следующие обозначения: 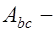 площадь сжатой зоны бетона;
площадь сжатой зоны бетона; 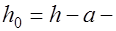 рабочая высота сечения;
рабочая высота сечения; 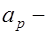 расстояние от центра тяжести напрягаемой арматуры в растянутой зоне до крайнего растянутого волокна сечения;
расстояние от центра тяжести напрягаемой арматуры в растянутой зоне до крайнего растянутого волокна сечения; 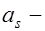 то же, но для арматуры площадью
то же, но для арматуры площадью 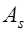 ;
; 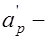 расстояние от центра тяжести напрягаемой арматуры площадью
расстояние от центра тяжести напрягаемой арматуры площадью 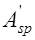 до крайнего сжатого волокна сечения;
до крайнего сжатого волокна сечения; 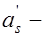 то же, но для арматуры
то же, но для арматуры 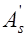 ;
; 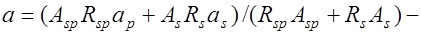 расстояние от общего центра тяжести напрягаемой арматуры
расстояние от общего центра тяжести напрягаемой арматуры 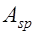 и ненапрягаемой арматуры
и ненапрягаемой арматуры 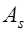 .
.
Действие изгибающего момента от расчетных нагрузок 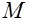 приводит к возникновению в нормальных сечениях внутренних усилий. Так как сечение до разрушения находится в равновесии, то из условия равенства нулю суммы проекции всех нормальных усилий на продольную ось элемента имеем:
приводит к возникновению в нормальных сечениях внутренних усилий. Так как сечение до разрушения находится в равновесии, то из условия равенства нулю суммы проекции всех нормальных усилий на продольную ось элемента имеем:
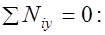
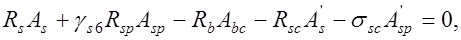 (12.1)
(12.1)
где 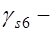 коэффициент условия работы, учитывающий возможность превышения напряжений в арматуре
коэффициент условия работы, учитывающий возможность превышения напряжений в арматуре 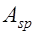 над
над 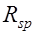 .
.
Из уравнения (12.1) можно получить площадь сечения бетона сжатой зоны 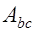 , а по ней – высоту сжатой зоны бетона
, а по ней – высоту сжатой зоны бетона 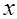 .
.
Согласно положениям метода расчета по предельным состояниям прочность нормального сечения элемента будет обеспечена, если изгибающий момент от внешних расчетных нагрузок 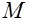 не будет превышать расчетную несущую способность того же сечения, выраженную в виде обратно направленного момента внутренних усилий
не будет превышать расчетную несущую способность того же сечения, выраженную в виде обратно направленного момента внутренних усилий 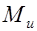 , то есть
, то есть 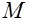
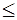
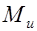 . Значения изгибающих моментов определяются относительно оси
. Значения изгибающих моментов определяются относительно оси 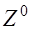 , перпендикулярной плоскости изгиба ХУи переходящей через общий центр тяжести растянутой арматуры
, перпендикулярной плоскости изгиба ХУи переходящей через общий центр тяжести растянутой арматуры 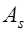 и
и 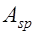 . Тогда условие прочности выразится неравенством:
. Тогда условие прочности выразится неравенством:
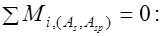
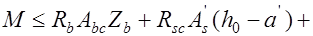
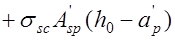 (12.2)
(12.2)
где 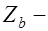 плечо внутренней пары сил или расстояние от центра тяжести площади сжатой зоны бетона до центра тяжести сечения растянутой арматуры.
плечо внутренней пары сил или расстояние от центра тяжести площади сжатой зоны бетона до центра тяжести сечения растянутой арматуры.
В предельном состоянии напряжения в арматуре сжатой зоны 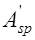 определяются из условия предельной сжимаемости бетона по формуле
определяются из условия предельной сжимаемости бетона по формуле
 , (12.3) где
, (12.3) где 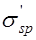 определяется при коэффициенте точности натяжения
определяется при коэффициенте точности натяжения 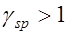 .
.
Если в сечениях изгибаемых элементов предусматриваются все виды арматуры 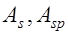 и
и 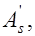
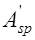 , то такие сечения называются сечениями с двойной арматурой и смешанным армированием, если в сечении отсутствует
, то такие сечения называются сечениями с двойной арматурой и смешанным армированием, если в сечении отсутствует 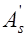 и
и 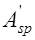 , то оно называется сечением с одиночной арматурой. При отсутствии того или иного вида арматуры из расчетных формул (12.1), (12.2) выпадают соответствующие члены. Соотношений (12.1) – (12.3) вполне достаточно, чтобы провести расчет прочности нормального сечения изгибаемых элементов. Однако зависимости (12.1) и (12.2) получены при условии
, то оно называется сечением с одиночной арматурой. При отсутствии того или иного вида арматуры из расчетных формул (12.1), (12.2) выпадают соответствующие члены. Соотношений (12.1) – (12.3) вполне достаточно, чтобы провести расчет прочности нормального сечения изгибаемых элементов. Однако зависимости (12.1) и (12.2) получены при условии 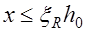 . Если это условие не выполняется, то высота сжатой зоны
. Если это условие не выполняется, то высота сжатой зоны 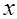 и напряжения в растянутой напрягаемой арматуре
и напряжения в растянутой напрягаемой арматуре 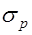 и в ненапрягаемой
и в ненапрягаемой 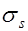 определятся из совместного решения уравнений:
определятся из совместного решения уравнений:
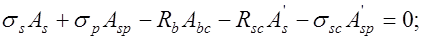
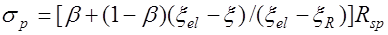 при
при 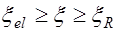 ;
;
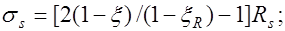
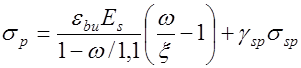 при
при 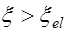 ,
,
где 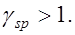
Следует заметить, что в последней редакции СНиП2.03.01-84* при 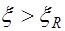 для определения
для определения 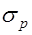 и
и 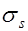 рекомендована единая эмпирическая формула
рекомендована единая эмпирическая формула
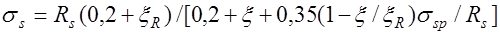 . (12.4)
. (12.4)
Для элементов, изготовленных из бетонов классом В30 и ниже с ненапрягаемой арматурой классов А-I, А-II, А-III, Вр-I при 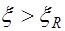 СНиП2.03.01-84* допускает проводить расчет прочности по формулам (12.1) и (12.2) заменив при этом
СНиП2.03.01-84* допускает проводить расчет прочности по формулам (12.1) и (12.2) заменив при этом 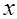 на
на 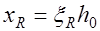 .
.
12.2. РАСЧЕТ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ НОРМАЛЬНОГО СЕЧЕНИЯ ПРЯМОУГОЛЬНОЙ ФОРМЫ С ОДИНОЧНОЙ НЕНАПРЯГАЕМОЙ АРМАТУРОЙ. ТИПЫ ЗАДАЧ
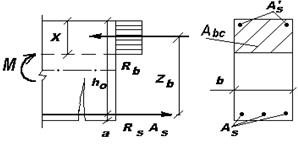
В стадии разрушения напряженное состояние элемента представляется следующим образом (рис. 12.2). В этом случае площадь сжатой зоны бетона определится следующим образом 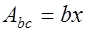 , а плечо внутренней пары сил –
, а плечо внутренней пары сил – 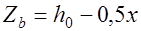 , где
, где 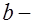 ширина сечения. Тогда условия прочности (12.1) и (12.2) примут вид:
ширина сечения. Тогда условия прочности (12.1) и (12.2) примут вид:
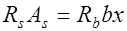 ; (12.5)
; (12.5)
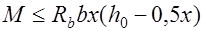 . (12.6)
. (12.6)
Следует заметить, что вместо условия прочности (12.6) иногда удобно пользоваться уравнением моментов, вычисленных относительно оси, проходящей через центр тяжести сжатой зоны:
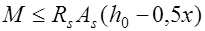 , (12.7)
, (12.7)
Таким образом, из уравнения (12.5) можно определить 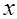 , а из выражения (12.6) – прочность сечения, а из неравенства (12.7) – определить требуемую площадь сечения арматуры, обеспечивающую прочность нормального сечения. Соотношения (12.5) – (12.7) можно привести к более удобному виду, подставив
, а из выражения (12.6) – прочность сечения, а из неравенства (12.7) – определить требуемую площадь сечения арматуры, обеспечивающую прочность нормального сечения. Соотношения (12.5) – (12.7) можно привести к более удобному виду, подставив 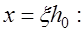
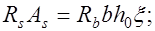
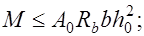
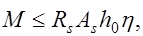 (12.8) где
(12.8) где 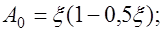
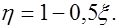
Преобразуем первое уравнение (12.8) следующим образом 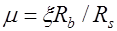 , где
, где 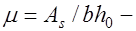 коэффициент армирования сечения, то есть отношение площади сечения арматуры к площади поперечного сечения. Отсюда очевидно можно установить максимально допустимое содержание растянутой арматуры, заменив
коэффициент армирования сечения, то есть отношение площади сечения арматуры к площади поперечного сечения. Отсюда очевидно можно установить максимально допустимое содержание растянутой арматуры, заменив 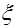 на
на 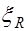 :
: 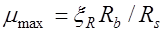 .
.
В СНиП2.03.01-84* установлены минимально допустимые значения коэффициентов армирования 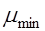 , которые необходимо учитывать при проектировании с целью повышения надежности конструкций. Для изгибаемых элементов
, которые необходимо учитывать при проектировании с целью повышения надежности конструкций. Для изгибаемых элементов 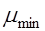 =0,0005.
=0,0005.
Расчетные формулы (12.5) – (12.8) получены для случая 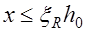 . Если это условие не выполняется, то необходимо повысить класс бетона, либо увеличить высоту сечения элемента, либо использовать двойное армирование. В противном случае высоту
. Если это условие не выполняется, то необходимо повысить класс бетона, либо увеличить высоту сечения элемента, либо использовать двойное армирование. В противном случае высоту 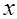 следует определять не из условия (12.5), а из выражения
следует определять не из условия (12.5), а из выражения 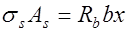 , где
, где 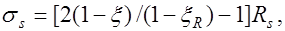
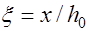 , или учитывая выражение (12.4) -
, или учитывая выражение (12.4) - 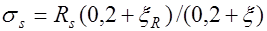 .
.
При расчете прямоугольных сечений с одиночным армированием возможны два типа задач: а) известны геометрические параметры сечения 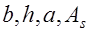 , прочностные характеристики материалов
, прочностные характеристики материалов 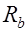 ,
, 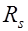 , изгибающий момент от расчетных нагрузок
, изгибающий момент от расчетных нагрузок 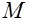 . Требуется проверить достаточна ли прочность сечения; б) известны размеры сечения, прочностные характеристики, но не известна площадь сечения арматуры
. Требуется проверить достаточна ли прочность сечения; б) известны размеры сечения, прочностные характеристики, но не известна площадь сечения арматуры 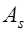 . Требуется определить площадь сечения арматуры
. Требуется определить площадь сечения арматуры 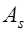 . Решение задач первого типа выполняется согласно алгоритму, приведенному в блок-схеме 12.1, а решение задач второго типа – по
. Решение задач первого типа выполняется согласно алгоритму, приведенному в блок-схеме 12.1, а решение задач второго типа – по
 |  | ||
блок-схеме 12.2.
Рис. 12.1 Рис. 12.2
Блок-схема 12.1
|


 | |||
| |||
|

|


|

|
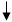 ДА
ДА
 |



|

|


 НЕТ
НЕТ
 | |||||
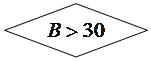 | |||||
 | |||||





 НЕТ ДА
НЕТ ДА


|

|

|
|

|
ДА
НЕТ
Блок-схема 12.2
|

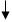 | |||
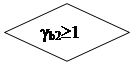 | |||
|
|

|
|

|
 ДА
ДА
 |
|
 НЕТ
НЕТ
 | |||||
 | |||||
| |||||



|

|
|

НЕТ ДА



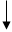

|

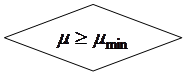

|
ДА
НЕТ
| <== предыдущая лекция | | | следующая лекция ==> |
| КОНСТРУКТИВНЫЕ ОСОБЕННОСТИ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ И ИХ РАБОТА | | | РАСЧЕТ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ПО ПРОЧНОСТИ НОРМАЛЬНОГО СЕЧЕНИЯ ПРЯМОУГОЛЬНОЙ ФОРМЫ С ДВОЙНОЙ НЕНАПРЯГАЕМОЙ АРМАТУРОЙ. ТИПЫ ЗАДАЧ |
Дата добавления: 2018-09-24; просмотров: 1434;