Разветвленные цепи. Правила Кирхгофа. Электронная теория проводимости.

Закон Ома для неоднородного участка цепи. Закон Ома для замкнутой цепи.

Разветвленные цепи. Правила Кирхгофа. Электронная теория проводимости.

Мы часто пользуемся понятием электрический ток, не задумываясь, что оно означает. Электрическим током называется направленное движение электрических зарядов. Чтобы можно было говорить об электрическом токе, нужно, во-первых, иметь носители зарядов, а во-вторых, требуется электрическое поле, энергия которого тратилась бы на их направленное перемещение в пространстве. В проводнике под действием электростатического поля свободные положительные электрические заряды перемещаются по полю, а отрицательные электрические заряды – против поля. Ток в проводнике при этом называется током проводимости. Поскольку на перемещение зарядов затрачивается энергия поля, необходимо, чтобы поле постоянно подпитывалось. За направление тока принято считать движение положительных зарядов.

Количественно электрический ток характеризуется силой тока – количеством зарядов, проходящих через поперечное сечение проводника в единицу времени

I = dQ/dt. (3.2.1)

Если сила тока и его направление не изменяются во времени, ток называется постоянным. Для него

I = Q/t. (3.2.2)

Единицей измерения тока является ампер (А): 1 А = 1 Кл/с.

Сила тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока, называется плотностью тока

j = dI/dS, (3.2.3)

которая измеряется в А/м².

Положительные заряды в электростатическом поле перемещаются от точек с более высоким потенциалом к точкам с меньшим потенциалом. Это ведет к выравниванию потенциалов и к исчезновению тока. Значит, для того чтобы ток мог течь постоянно, необходимы устройства, которые называются источниками тока. Силы, которые действуют на заряды со стороны источников тока, как правило, являются силами неэлектростатического происхождения, их называют сторонними силами. Часто в качестве источников тока используются гальванические гальванические элементы, в которых сторонние силы возникают за счет энергии химической реакции между их электродами и электролитами. Другим типом источников тока служат генераторы, в которых эти силы возникают за счет энергии механического вращения ротора. Источник тока можно уподобить насосу, который перекачивает жидкость.

Сторонние силы совершают работу по перемещению зарядов. Физическая величина, которая определяется работой по перемещению сторонними силами единичного положительного заряда, называется электродвижущей силой (ЭДС)

Є = A/Q₀. (3.2.4)

ЭДС измеряется в вольтах, как и потенциал.

Сторонняя сила F_ст, действующая на заряд Q₀, может быть выражена через напряженность Е_стполя сторонних сил следующим образом F_ст = Е_стQ₀, поэтому работа сторонних сил по перемещению заряда Q₀ на замкнутом участке цепи на расстояние dl будет равна интегралу по замкнутому контуру от Е_стdl, умноженному на заряд Q₀. Тогда с учетом 3.2.4 можно записать, что ЭДС

Є = 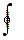Е_стdl. (3.2.5)

Это означает, что ЭДС, действующая в замкнутой цепи, равна циркуляции вектора напряженности поля сторонних сил. Если ЭДС действует только на определенном участке 1 – 2, то для нее можно записать

Є₁₂ = 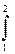Е_стdl. (3.2.6)

Кроме сторонних сил, на заряд действуют также силы электростатического поля F_e = Q₀E. Поэтому результирующая сила, действующая на заряд Q₀, будет равна F= F_ст +F_e = Q₀(Е_ст +E), и тогда работа результирующей силы по перемещению заряда Q₀ на участке 1 – 2 может быть выражена следующим образом:

А₁₂ = Q₀Є₁₂ + Q₀(φ₁ – φ₂). (3.2.7)

Для замкнутой цепи работа электростатических сил по перемещению заряда равна нулю, поэтому А₁₂ = Q₀Є₁₂.

Из 3.2.7 следует, что работа по перемещению единичного положительного заряда (Q₀ = 1 Кл), совершаемая суммарным полем электростатических и сторонних сил, равна сумме ЭДС и разности потенциалов, эта физическая величина называется напряжением

U = Є₁₂ + (φ₁ – φ₂). (3.2.8)

Напряжение на концах участка цепи равно разности потенциалов, если на нем не действует ЭДС.

Немецкий физик Г. Ом эмпирически установил, что сила тока I, который протекает по однородному металлическому проводнику (т. е проводнику, в котором не действуют сторонние силы, пропорциональна напряжению на его концах

I = U/R, (3.2.9)

где R – электрическое сопротивление проводника. Уравнение 3.2.9 является математическим выражением закона Ома для участка цепи. Единицей измерения сопротивления является 1 Ом, под которым понимают сопротивление такого проводника, в котором при напряжении в 1 В течет постоянный ток 1 А. Величина (G = 1/R), обратная электрическому сопротивлению, называется электрической проводимостью, которая измеряется в сименсах (См): 1 См – проводимость участка цепи с сопротивлением 1 Ом.

Установлено, что сопротивление однородного металлического проводника зависит от его размеров и формы, но – главное – оно прямо пропорционально его длине l и обратно пропорционально площади S его поперечного сечения

R = ρl/S. (3.2.10)

Коэффициент пропорциональности ρ в 3.2.10 называется удельным электрическим сопротивлением.Единицейизмерения удельного электрического сопротивления является Ом-метр. Каждый металл характеризуется своим значением удельного электрического сопротивления: 1.6*10^-8 Ом*м – серебро, 1.7*10^-8 Ом*м – медь, 2.6*10^-8 Ом*м – алюминий.

Как показывает опыт, удельное электрическое сопротивление, а значит, и сопротивление проводника линейно зависят от температуры

ρ = ρ₀(1 + αt)

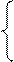R = R₀(1 + αt), (3.2.11)

где ρ₀ и R₀ - их значения при 0 ⁰С, а α – температурный коэффициент сопротивления, близкий для чистых проводников к (1/273) К^-1. Подставив это значение в 3.2.11, получим, что R = αR₀T, где Т – термодинамическая температура.

Указанная выше температурная зависимость сопротивления обусловлена тем, что с ростом температуры движение электронов (так называемый «электронный газ») в металле становится все более хаотическим, растут скорости их перемещения между соударениями, поэтому упорядочить их движение при помещении проводника в электростатическое поле становится все труднее. Разумеется, при понижении температуры наблюдается обратный эффект: падение сопротивления проводника. Более того, сопротивление многих металлов при очень низких температурах (до 20 К) – для каждого металла эта температура, называемая критической, своя – скачкообразно уменьшается до нуля, т. е. металл становится сверхпроводником. Это явление используют в сверхпроводящих магнитах, однако тормозом к более широкому использованию металлических сверхпроводников является очень низкие значения их критических температур. В последнее время, правда, разработаны керамические материалы, у которых критические температуры превышают 100 К. Охладить до таких температур, скажем, обмотки магнита, зачастую имеющего достаточно большой объем, уже, конечно, гораздо проще, чем до 20 К или до еще более низких температур.

Явление сверхпроводимости используется для достаточно точного (с точностью до 0.003 К) измерения сверхнизких температур. Для этого, конечно, надо точно знать температурную зависимость конкретных сверхпроводников.

Коль скоро электрические заряды перемешаются по однородному проводнику, значит, над ними совершается работа. Представим проводник, к концам которого приложено напряжение U.

За промежуток времени dt через сечение проводника переносится заряд dq = Idt. Тогда работа по перемещению зарядов

dA = Udq = IUdt = IIRdt = I²Rdt = (U²/R)dt. (3.2.12)

Отсюда мощность тока

dA/dt = IU = I²R = U²/R. (3.2.13)

Единица измерения мощности – ватт. В быту применяют внесистемную единицу работы тока – кВт*ч. 1 Вт*ч = 3600 Вт*с = 3.6 *10³ Дж. 1 кВт*ч = 3.6*10⁶ Дж.

Если ток протекает по закрепленному (неподвижному) проводнику, то вся работа тока идет на его нагревание, поэтому по закону сохранения энергии

dQ = dA = IUdt = IIRdt = I²Rdt = (U²/R)dt. (3.2.14)

Теперь вернемся к выражению 3.2.9, оно позволяет найти ток через однородный участок электрической цепи. А как его определить для неоднородного участка, включающего в себя и источник ЭДС? Рассмотрим участок цепи 1 – 2, на котором действует ЭДС Є₁₂ и к концам которогоприложена разность потенциалов (φ₁ – φ₂). Если проводники неподвижны, то работа А₁₂ электростатических и сторонних сил по перемещению зарядов равна теплоте, которая выделяется на участке. В случае перемещения заряда Q₀ работа

А₁₂ = Q₀Є₁₂ + Q₀(φ₁ – φ₂). (3.2.15)

Если ЭДС способствует перемещению положительного заряда, то ее считают положительной, если же препятствует – отрицательной. За время t в проводнике выделяется теплота

Q = I²Rt = IR(It) = IRQ₀. (3.2.16)

Сравнивая 3.2.15 и 3.2.16, после сокращения Q₀ получаем

IR = φ₁ – φ₂ + Є₁₂, (3.2.17)

Откуда выражение для тока приобретет следующий вид

I = (φ₁ – φ₂ + Є₁₂)/R. (3.2.18)

Выражения 3.2.17 и 3.2.18 отражают закон Ома для неоднородного участка цепиили обобщенный закон Ома.

Если на участке источник тока отсутствует (Є₁₂ = 0 В), то мы получаем закон Ома для однородного участка цепи I = (φ₁ – φ₂)/R = U/R. Если же цепь замкнута, то точки 1 и 2 совпадают, то φ₁ = φ₂, тогда I = Є/R, где R – суммарное сопротивление цепи (R = r + R₁, причем r – это внутреннее сопротивление источника ЭДС, а R₁ – сопротивление внешней цепи). Поэтому для замкнутой цепи закон Ома приобретает вид I = Є/(r + R₁). Если цепь разомкнуть, тока в ней не будет, поэтому из 3.2.18 следует, что Є₁₂ = φ₂ – φ₁, а это значит, что ЭДС в разомкнутой цепи равна разности потенциалов на ее концах.

Обобщенный закон Ома позволяет определить ток на неоднородном участке цепи. На практике, однако, приходится сталкиваться с разветвлением цепей. Контура, из которых могут складываться разветвленные цепи, могут содержать по несколько источников ЭДС. Чтобы решить такую сложную задачу, пользуются правилами немецкого физика Г. Кирхгофа.

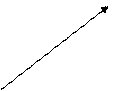
Любая точка разветвления называется узлом, если в ней сходится не менее 3 проводников. Ток, входящий в узел, считается положительным, а ток, выходящий из него, – отрицательным. Первое правило Кирхгофагласит: алгебраическая сумма токов, сходящихся в узле, равна нулю.

I₁ I₅

I₂

I_{3 I4}

Рис. 3.2.1.

Для узла, представленного на рис. 3.2.1, первое правило Кирхгофа будет выглядеть следующим образом: I₁ – I₂ + I₃ – I₄ – I₅ = 0. В основе этого правила лежит закон сохранения электрического заряда: в случае установившегося постоянного тока не должно происходить накопление заряда ни в одной точке контура, иначе токи не оставались бы постоянными.

Для установления второго правила Кирхгофарассмотрим контур, состоящий из трех участков с точками разветвления А, В и С. Будем считать направление обхода контура по часовой стрелке А – В – С – А положительным. Тогда, если направление тока на рассматриваемом участке совпадает с направлением обхода контура, то ток считается положительным, если противоположен ему, - отрицательным. На участке АВ течет ток I₁ от А к В (по часовой стрелке, ток положительный), сопротивление участка равно R₁, на нем действует ЭДС Є₁; на участке ВС течет ток I₂ от С к В (против часовой стрелки, ток отрицательный), сопротивление участка R₂, ЭДС Є₂; на участке СА течет ток I₃ от С к А (по часовой стрелке, ток положительный), сопротивление R₃, ЭДС Є₃. Источники ЭДС считаются положительными, если они создают ток, совпадающий по направлению с направлением обхода контура, и наоборот. Тогда, применив закон Ома для трех участков контура, можем записать

I₁R₁ = φ_А – φ_В + Є₁,

– I₂R₂ = φ_В – φ_С – Є₂,

I₃R₃ = φ_С – φ_А + Є₃. 3.2.19

Складывая члены, представленные в левой и правой частях этих уравнений, получим второе правило Кирхгофа: в любом замкнутом контуре разветвленной электрической сети алгебраическая сумма произведений токов I_i на сопротивления R_i соответствующих участков контура равна алгебраической сумме ЭДC, имеющихся в этом контуре. Поскольку все потенциалы в правых частях уравнений при суммировании встречаются дважды с противоположными знаками, поэтому они исчезают, а остается только алгебраическая сумма ЭДС:

I₁R₁ – I₂R₂ + I₃R₃ = Є₁ – Є₂ + Є₃. 3.2.20

Применение правил Кирхгофа к сложным электрическим цепям сводится к выполнению следующих правил:

1. Выбирается произвольное направление токов на участках цепи. Если в результате решения задачи искомый ток получился положительным, значит, его направление было выбрано правильно, а если отрицательным, то его истинное направление противоположно выбранному.

2. Выбирается направление обхода контура, произведение IR считается положительным, если ток на данном участке контура совпадает по направлению с направлением обхода, и наоборот. ЭДС, которые действуют в выбранном направлении обхода, считаются положительными, а ЭДС, действующие против направления обхода, – отрицательными.

3. Составляются уравнения закона Ома для каждого участка контура, в них должны входить все сопротивления и все ЭДС цепи. При этом уравнения для каждого контура должны содержать хотя бы один член, который не содержится в других уравнениях.

Теперь вернемся к вопросу о природе носителей зарядов, направленное движение которых называется электрическим током. По представлениям двух физиков – П. Друде из Германии и Х. Лоренца из Нидерландов – в случае металлов этими носителями являются свободные электроны. Это было доказано опытами по определению удельного заряда (отношение заряда к массе) носителей тока в металлах и электронов, движущихся в вакууме. Оказалось, что значения удельного заряда для тех и других совпали. Электроны слабо связаны с катионами кристаллической решетки, находящимися в ее узлах, поэтому электроны в отсутствии поля хаотически движутся в объеме металла, образовывая своеобразный «электронный газ». При своем движении электроны сталкиваются с катионами, в результате чего устанавливается термодинамическое равновесие между ними и кристаллической решеткой.

При наложении внешнего электрического поля на металлический проводник, кроме хаотического движения электронов, наблюдается и их упорядоченное движение, т. е. электрический ток.

Контрольные вопросы

1. Что называется электрическим током и каковы условия его возникновения?

2. Каков физический смысл понятия «сила тока»? В каких единицах она измеряется?

3. Когда электрический ток называют постоянным?

4. Что такое плотность тока и какова единица ее измерения?

5. Что понимают под электродвижущей силой?

6. Как связаны друг с другом напряжение, электродвижущая сила и разность потенциалов на концах участка цепи?

7. Как формулируется закон Ома для однородного металлического проводника?

8. Какова связь между электрическим сопротивлением и электрической проводимостью и каковы единицы их измерения?

9. Как зависит электрическое сопротивление от температуры?

10. При каких условиях проводник превращается в сверхпроводник?

11. Как вычисляется работа по перемещению заряда на участке цепи, на котором действует ЭДС и к концам которого приложена разность потенциалов?

12. Как определить количество теплоты, выделяющейся в проводнике при протекании по нему электрического поля?

13. Как формулируется первое правило Кирхгофа для узла электрической цепи?

14. Как пользоваться вторым правилом Кирхгофа при расчете замкнутых контуров разветвленной электрической цепи?

15. Какие носители зарядов определяют электропроводность металлического проводника?