Нормированное отклонение t .
Использование среднего квадратичного отклонения позволяет выразить в относительном выражении степень отклонения какого – либо члена совокупности от средней арифметической данного ряда.
Для этого берут разность между значением данного варианта x и значением среднего арифметического 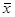 и относят эту разность к среднему квадратичному отклонению
и относят эту разность к среднему квадратичному отклонению 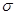 . Полученное в результате такого отношения выражение
. Полученное в результате такого отношения выражение 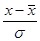 называется нормированным отклонением t данного члена совокупности от среднего арифметического в долях
называется нормированным отклонением t данного члена совокупности от среднего арифметического в долях  .
.
Чем больше величина нормированного отклонения, тем дальше от 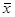 отстоит данный вариант. Минимальное и максимальное значение вариантов имеют нормированное отклонение, равное
отстоит данный вариант. Минимальное и максимальное значение вариантов имеют нормированное отклонение, равное 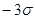 и
и 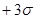 .
.
Степень свободы.
При рассмотрении понятия дисперсии и среднего квадратического отклонения мы столкнулись с величиной n-1, которая получила особое название – число степеней свободы. В дальнейшем мы будем обозначать эту величину буквой 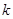 . Объясним подробнее его значение.
. Объясним подробнее его значение.
Рассмотрим некоторый вариационный ряд, в котором имеется n вариант. При известном значении средней выборочной этого ряда каждая отдельная варианта жестко связана с остальными n – 1 вариантами. То есть в данном случае имеется n – 1 степеней свободы. Так, например, если известно, что два кролика в сумме весят 7 кг, а один из них весит 3,5 кг, то вес второго уже точно определен весом первого, то есть имеется 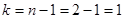 степеней свободы. Если известно, что 10 кроликов весят вместе 55 кг (т.е. выборочная средняя равна 5,5), то вес одного определяется весом девяти других, то есть имеется
степеней свободы. Если известно, что 10 кроликов весят вместе 55 кг (т.е. выборочная средняя равна 5,5), то вес одного определяется весом девяти других, то есть имеется 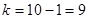 степеней свободы.
степеней свободы.
Дата добавления: 2017-02-20; просмотров: 1029;
