Теплоизоляция резервуаров для хранения нефтепродуктов

Согласно технических условий эксплуатации многие типы резервуаров для хранения нефти, а в особенности мазута, требуют подогрева. Мазут, например, должен быть подогрет до температуры 80 ^оС. Подогрев осуществляется через днище с помощью перегретого пара. Для этих целей под днищем прокладывается система трубопроводов или электрических змеевиков. Существует способ подогрева с помощью электрических змеевиков, вмонтированных во внешнюю обшивку резервуара. В любом случае для сохранения некоторое время постоянной температуры хранимой жидкости наружная поверхность резервуара утепляется.

Процесс теплообмена осуществляется естественной конвекцией протекающей в ограниченном пространстве [10]. Согласно упрощенной схеме (см. рис. 9.11) одновременно происходят два процесса: нагревание у горизонтальной поверхности (днища) с поднятием кверху нагретых масс и охлаждение жидкости у стенки (и покрытия) с опусканием вниз охлаждающихся масс. По центральной вертикале резервуара может установиться температура t₁, на внутренней поверхности стенок она окажется равной t₂. Тогда перепад температур составит 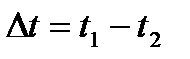. Средняя температура жидкой среды определится как .

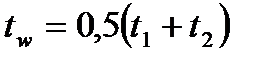Однако к таких условиях установить правильную закономерность изменения коэффициента теплоотдачи отдельно для нагревания и охлаждения жидкости с учетом особенностей циркуляции практически невозможно. Поэтому в инженерных расчетах сложный процесс теплообмена принято рассматривать как элементарное явление передачи тепла путем теплопроводности, используя при этом понятие эквивалентного коэффициента теплопроводности .

t_е

Н R_o

t_w

δ_k 2 δ δ_k

Рис. 9.11 - Упрощенная схема теплообмена в резервуаре

Величина эквивалентного коэффициента теплопроводности устанавливается простой зависимостью вида

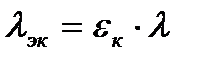, (9.2)

где 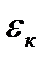- коэффициент конвекции;

λ - коэффициент теплопроводности жидкости при данной температуре, Вт/(м·^оС).

Так как циркуляция жидкости обусловлена разностью плотностей нагретых и холодных частиц и определяется критерием Gr·Pr, то и величина 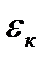является функцией этого аргумента. Функция произведения этих критериев представляет собой критерий Нуссельта, т.е. Nu = F(Gr·Pr).

Критерий Грасгофа (Gr ) определяется зависимостью

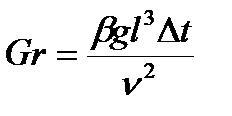, (9.3)

критерий Прандтля (Pr) имеет вид

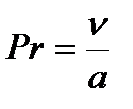, (9.4)

где β – коэффициент температурного расширения, (^оС^-1);

а - коэффициент температуропроводности, м²/с, ;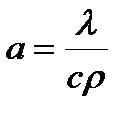

с - удельная теплоемкость жидкости, Дж/кг·^оС;

ρ - плотность жидкости, кг/м³;

ν – кинематическая вязкость жидкости, м²/с;

g – ускорение силы тяжести, м/с²;

l - определяющий линейный размер (в данном случае – высота резервуара Н), м;

Δt – температурная разность, ^оС, между поверхностью и жидкостью на достаточном удалении от поверхности (можно принять температуру на вертикальной оси центра резервуара).

В приближенных расчетах по данным М.А. Михеева [10] для области значений аргумента Gr·Pr > 10³ для определения величины 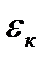используется зависимость вида

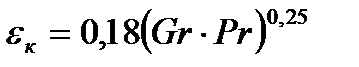. (9.5)

Окончательный вид формулы (9.5) следующий:

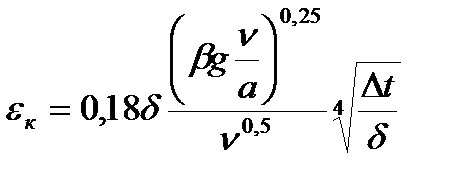. (9.6)

В этой формуле δ - радиус резервуара, м.

Удельное количество тепла, q, Вт/м², передаваемого 1 м² внутренней вертикальной поверхности представляется зависимостью вида

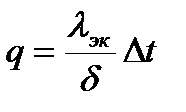. (9.7)

Величина сопротивления теплопередаче внешней теплоизоляции, R_o, м²∙^оС/Вт, может быть найдена из соотношения

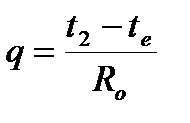. (9.8)

В формуле (9.8) t_e –температура наружного воздуха. Температура внутренней среды определяется техническим заданием, температура наружного воздуха равняется средней за год.

Приравняв правые части формул (9.7) и (9.8), получим 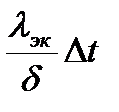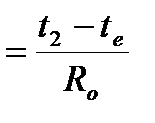, откуда

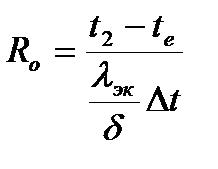. (9.9)

Сопротивление теплопередаче теплоизолирующего слоя (для варианта одного слоя однородного утеплителя) может быть представлено как сумма его термического сопротивления ( 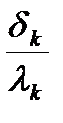) и сопротивления теплоотдаче у наружной поверхности ( 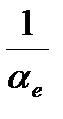), т.е.

R_{o =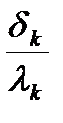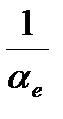} + , (9.10)

где λ_k – коэффициент теплопроводности утеплителя, Вт/(м∙^оС).

Из совместного решения уравнений (9.9) и (9.10) находится толщина утеплителя

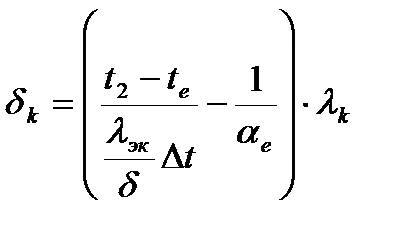. (9.11)

В формулах (9.10) и (9.11) величина коэффициента теплоотдачи (α_e, Вт/(м²∙^оС)) у наружной поверхности может быть принята согласно Приложения 9 [11].

Расчет по формуле (9.11) возможен, если заданы параметры внутренней среды (Δt, t₂), а также точно указаны теплофизические характеристики нефтепродуктов.

Согласно СНиП 2.04.14–88 [11] расчет толщины теплоизоляционного слоя производится по нормативной плотности теплового потока, q, Вт/м², проходящего через изолированную поверхность.

Толщина теплоизоляционного слоя d_k, м, определяется по формуле

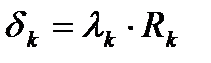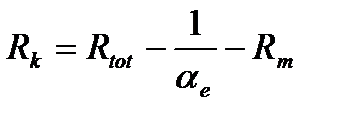; , (9.12)

где l_k - теплопроводность теплоизоляционного слоя, Вт/(м×°С);

R_k - термическое сопротивление теплоизоляционной конструкции, м²×°С/Вт;

R_tot - сопротивление теплопередаче теплоизоляционной конструкции, м²×°С/Вт;

a_e - коэффициент теплоотдачи от наружной поверхности изоляции, принимаемый по справочному приложению 9 [11], во всех случаях равен 29 Вт/(м²×°С);

R_m - термическое сопротивление неметаллической стенки объекта, (если такая имеется в наличие), м²×°С/Вт.

Величина R_tot в зависимости от исходных условий определяется по формуле

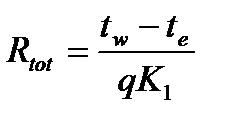, (9.13)

где t_w – средняя температура вещества, °С;

t_e - температура окружающей среды, принимается средней за год [12], °С;

K₁ - коэффициент, принимаемый по обязательному приложению 10 [11], для Украины K₁ равен 1.

Дополнительное термическое сопротивление плоских и криволинейных неметаллических поверхностей оборудования определяется по формуле

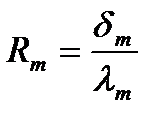, (9.14)

где d_m и λ_m – соответственно толщина и коэффициент теплопроводности ограждения.