Механическое сглаживание по скользящим средним

Методы сглаживания временных рядов

Очень часто уровни экономических рядов динамики колеблются. При этом тенденция развития экономического явления во времени скрыта случайными отклонениями значений ряда в ту или иную сторону. С целью более чёткого выявления тенденции развития исследуемого процесса производят сглаживание (выравнивание) временных рядов экономических показателей. Суть различных методов сглаживания сводится к замене фактических уровней временного ряда расчётными значениями, которые подвержены колебаниям в меньшей степени. Это способствует чёткому проявлению тенденции.

Методы сглаживания временных рядов делятся на две основные группы:

1) аналитическое выравнивание с использованием кривой, проведённой между конкретными уровнями ряда так, чтобы она отображала тенденцию, присущую ряду, и одновременно освобождала его от незначительных колебаний;

2) механическое выравнивание отдельных уровней временного ряда с использованием фактических значений соседних уровней.

Суть методов аналитического сглаживания основана на том математическом правиле, что через любые n точек, лежащих на плоскости, можно провести полином минимум (n – 1) степени так, что он будет проходить через все обозначенные точки.

Суть методов механического сглаживания заключается в том, что берётся несколько уровней ряда динамики, образующих интервал сглаживания. Для них подбирается полином, степень которого должна быть меньше числа уровней, входящих в интервал сглаживания. С помощью полинома определяются сглаженные значения уровней ряда в середине интервала сглаживания. Далее интервал сглаживания сдвигается на одно наблюдение вперёд, вычисляется следующее сглаженное значение и т.д.

Механическое сглаживание по скользящим средним

Самым простым методом механического сглаживания является сглаживание по простой скользящей средней. Метод называется так потому, что в его основе лежит вычисление простого среднего значения нескольких уровней ряда. Простое среднее скользит вдоль ряда динамики с шагом равным периоду наблюдений.

Сначала для временного ряда y_t определяется интервал сглаживания m, причём m < n. Если необходимо сгладить мелкие беспорядочные колебания, то интервал сглаживания берут по возможности большим; интервал сглаживания уменьшают, если нужно сохранить более мелкие колебания. Чем шире интервал сглаживания, тем в большей степени взаимопогашаются колебания, и тенденция развития носит более плавный характер. Чем сильнее колебания, тем шире должен быть интервал сглаживания. При одинаковых условиях рекомендуется использовать интервал сглаживания нечётной длины. Для первых m уровней временного ряда вычисляется их средняя арифметическая; это будет сглаженное значение уровня ряда, находящегося в середине интервала сглаживания.

Для вычисления сглаженных значений используется формула:

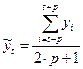(4.1),

где m = 2·p + 1 – интервал сглаживания временного ряда нечётной длины. В результате такой процедуры получаются (n – m + 1) сглаженных значений уровней ряда.

Процедуру сглаживания можно применять и для интервала сглаживания чётной длины. Особенно это актуально для анализа и прогнозирования явлений, имеющих сезонные колебания. При сглаживании сезонных процессов интервал сглаживания обязательно должен быть равен длине сезонной волны. В противном случае произойдёт искажение компонент временного ряда, в особенности, компоненты v_t. В случае, когда используется интервал сглаживания чётной длины, т.е. m = 2·p, применяется формула:

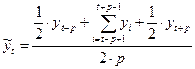(4.2).

В результате данной процедуры получаются (n – m) сглаженных значений уровней ряда.

В любом случае первые и последние p значений ряда не сглаживаются. Потерянные сглаженные значения уровней временного ряда находятся с помощью использования показателя среднего абсолютного прироста, найденного для первого и последнего интервалов сглаживания. Для восстановления потерянных наблюдений в начале временного ряда значение величины среднего абсолютного прироста, найденное для первого интервала сглаживания, вычитается из первого сглаженного значения. Получается сглаженное значение уровня ряда для y_p. Далее алгоритм повторяется до получения сглаженного значения y₁. Для восстановления потерянных наблюдений в конце временного ряда значение величины среднего абсолютного прироста, найденное для последнего интервала сглаживания, прибавляется к последнему сглаженному значению. Получается сглаженное значение уровня ряда для y_{n – p + 1}. Далее алгоритм повторяется до получения сглаженного значения y_n.

Ещё один недостаток метода простой скользящей средней заключается в том, что он может использоваться лишь для рядов, имеющих линейную тенденцию. Если для процесса характерно нелинейное развитие и необходимо сохранить изгибы тенденции, то применение простой скользящей средней нецелесообразно, т.к. это может привести к существенным искажениям. В таких случаях используется метод взвешенной скользящей средней.

Метод взвешенной скользящей средней отличается от метода простой скользящей средней тем, что уровни, входящие в интервал сглаживания, суммируются с разными весами. Это связано с тем, что аппроксимация исходного ряда в пределах интервала сглаживания осуществляется с использованием полинома не первой степени, как в методе простой скользящей средней, а степени, начиная со второй. Используется формула средней арифметической взвешенной:

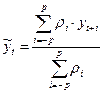(4.3),

где веса ρ_t симметричны относительно среднего значения и определяются с помощью метода наименьших квадратов. Эти веса рассчитаны для различных степеней аппроксимирующего полинома и различных интервалов сглаживания.

Единственным недостатком данного метода является потеря сглаженных наблюдений на концах экономического ряда динамики. Алгоритм восстановления пропущенных значений аналогичен описанному в методе простой скользящей средней.