Модели "спортивного" типа
Наиболее простыми являются модели "спортивного" типа, в которых интегральный показатель качества j i представляется как "сумма очков" (сумма элементов строки). В простейшем случае он имеет вид
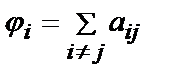 .
.
Альтернативные варианты упорядочиваются по мере убывания j i:
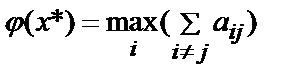 .
.
При построении матрицы А для модели "спортивного" типа могут быть использованы: простая структура, турнирная и кососимметричная калибровки.
Однако использование простой структуры не позволяет определить степень предпочтительности вариантов. Поэтому итоговые значения j i также следует рассматривать как значения шкалы порядка, не позволяющие определить, насколько одна из альтернатив предпочтительнее другой. В этом случае следует использовать другие модели упорядочивания.
Модель Брэдли - Терри (модель максимального правдоподобия)
Простейшая модель максимального правдоподобия, называемая моделью Брэдли - Терри, предполагает, что каждому варианту xi сопоставляется его сила j i. Причем считается, что вероятность превосходстваxi > xj прямо пропорциональна этой силе.
Р(xi > xj) = j i /(j i +j j) = 1 – Р(xj > xi).
После проведениясравнений пар (xi, xj) получают систему уравнений:
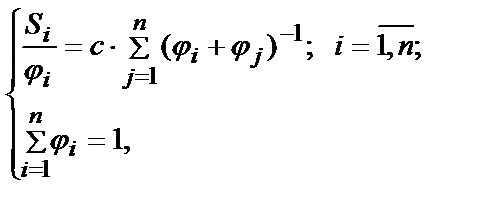
где 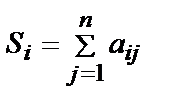 ,
, 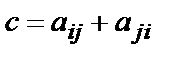 при турнирной калибровке и
при турнирной калибровке и 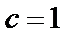 при простой структуре. Данная система решается итерационно. После получения значений j i варианты упорядочиваются по их значениям.
при простой структуре. Данная система решается итерационно. После получения значений j i варианты упорядочиваются по их значениям.
Рассмотренная модель используется для простых структур и турнирных калибровок.
Модель Бержа
В модели Бержа каждому альтернативному варианту ставится в соответствие цепочка так называемых интегрированных сил Рi (1), Рi (2),..., в которой сила k-го порядка Рi (k) определяется как сумма элементов i-й строки в матрице А k:
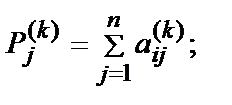
где k – степень, в которую возводится матрица А, 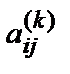 – элемент матрицы А k размерностью n´n.
– элемент матрицы А k размерностью n´n.
Показатель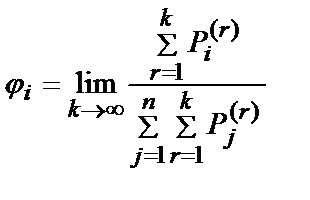 позволяет выполнить упорядочивание альтернатив xi. При этом скорость сходимости j i с ростом k велика. Поэтому для упорядочивания альтернатив достаточно пользоваться оценками j i при малых значениях k =2¸4. Данная модель может быть использована для простой структуры, турнирной и степенной калибровок.
позволяет выполнить упорядочивание альтернатив xi. При этом скорость сходимости j i с ростом k велика. Поэтому для упорядочивания альтернатив достаточно пользоваться оценками j i при малых значениях k =2¸4. Данная модель может быть использована для простой структуры, турнирной и степенной калибровок.
Рассмотрим пример решения задачи линейного упорядочивания с использованием модели Бержа для оценки значимости элементов технической структуры с целью обеспечения ее надежности.
Пусть, например, на начальном этапе проектирования необходимо определить значимость элементов структуры, представленной на рисунке 4.
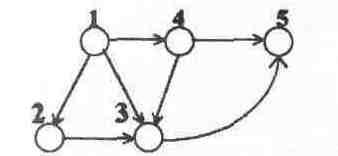
Рис. 4. Пример технической структуры
Стрелкой показано направление информационной связи между элементами структуры. Если элемент структуры xi связан с элементом структуры xj, то с точки зрения надежности функционирования xi > xj. Выходиз строя элемента xi приводит к невозможности работы элементаxj.
Использование простой структуры приводит к матрице А, А(2), А(3) вида (при этом 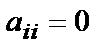 ):
):
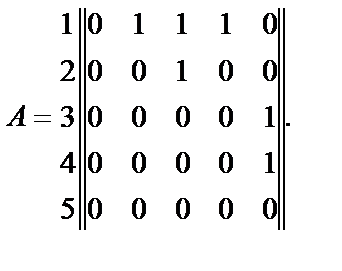
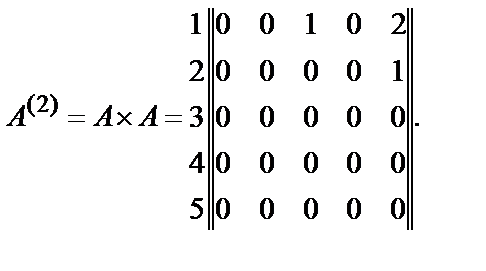
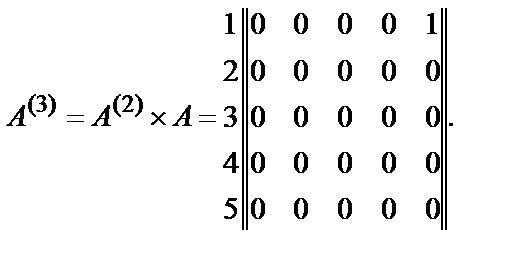
Вычислим 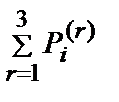 . Получим
. Получим 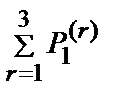 =7,
=7, 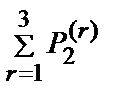 =2,
=2, 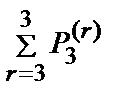 =
= 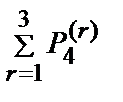 =1,
=1, 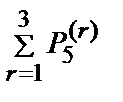 =0.
=0. 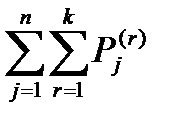 = 7 + 2 + 1 + 1 + 0 = 11. Тогда j1=7/11, j2=2/11, j3=1/11, j4=1/11, j5=0. В данном примере ji имеет смысл значимости (веса) надежности i–го элемента технической структуры для обеспечения ее надежности в целом.
= 7 + 2 + 1 + 1 + 0 = 11. Тогда j1=7/11, j2=2/11, j3=1/11, j4=1/11, j5=0. В данном примере ji имеет смысл значимости (веса) надежности i–го элемента технической структуры для обеспечения ее надежности в целом.
Эти значения позволяют произвести линейное упорядочивание важности элементов технической структуры для обеспечения ее надежности в целом.
Модель Ушакова
Стохастическая модель Ушакова используется для обработки матриц А, заданных в степенной и вероятностной калибровках. Матрица А преобразуется в вероятностную матрицу Р, произвольный элемент которой pij интерпретируется как вероятность превосходства xj надxi. В том случае, если задана вероятностная калибровка, то матрица Р получается из матрицы А путем транспонирования Р = АТ, т.к. значение aij в вероятностной калибровке указывает на вероятность того, что i-й вариант превосходит j-й.
Так как 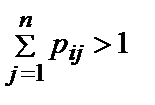 , то матрица Р преобразуется в матрицу
, то матрица Р преобразуется в матрицу 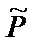 , элемент которой
, элемент которой 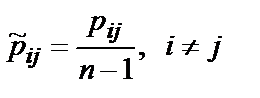 .
.
Для выполнения условия 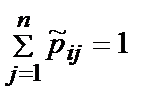 элементы главной диагонали матрицы
элементы главной диагонали матрицы 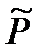 :
: 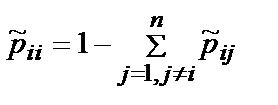 .
.
В этом случае матрица 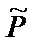 принимает смысл матрицы вероятностей перехода эргодической цепи Маркова, в которой один вариант соответствует одному состоянию. Напомним, что эргодическими называются такие цепи Маркова, у которых вероятности перехода системы в различные состояния (финальные вероятности каждого состояния) перестают меняться от шага к шагу, а, следовательно, существуют предельные вероятности переходов в каждое состояние, которые не зависят от исходного состояния. Финальные вероятности каждого состояния определяют значения интегральных показателей ji. Показатель jj=
принимает смысл матрицы вероятностей перехода эргодической цепи Маркова, в которой один вариант соответствует одному состоянию. Напомним, что эргодическими называются такие цепи Маркова, у которых вероятности перехода системы в различные состояния (финальные вероятности каждого состояния) перестают меняться от шага к шагу, а, следовательно, существуют предельные вероятности переходов в каждое состояние, которые не зависят от исходного состояния. Финальные вероятности каждого состояния определяют значения интегральных показателей ji. Показатель jj= 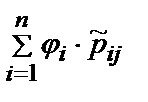 . Причем,
. Причем, 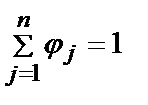 . В дальнейшем упорядочивание альтернативных вариантов производится в порядке убывания значений ji.
. В дальнейшем упорядочивание альтернативных вариантов производится в порядке убывания значений ji.
Дата добавления: 2018-06-28; просмотров: 439;
