Формальные модели линейного упорядочивания альтернатив
Если найден интегральный критерий, по которому можно упорядочить все альтернативы, то задача принятия решения сводится к задаче оптимизации.
Задачи линейного упорядочивания альтернатив при отсутствии интегрального критерия относятся к наиболее широкому классу задач принятия решений. Они определяют отношение порядка между всеми альтернативными вариантами, одновременно автоматически задавая лучшую и худшую альтернативы. В настоящее время накоплено достаточно большое число различных моделей упорядочения, каждую из которых целесообразно использовать в конкретных случаях. Все множества таких моделей можно разделить на два больших класса: формальные модели упорядочивания и модели, основанные на проведении экспертных процедур оценивания.
Основу формальных моделей линейного упорядочивания составляют графические модели, получаемые в результате выполнения процедур бинарного сравнения альтернативных вариантов (по парам) для их упорядочивания на основе использования языка бинарных отношений.
Пусть задано некоторое фиксированное множество объектов, которые сравниваются друг с другом с точки зрения их предпочтительности, желательности, важности и т.п., а результаты сравнения записываются в виде матрицы парных сравнений 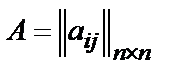 , отражающей возникающие бинарные отношения предпочтения и эквивалентности (или безразличия) на данном множестве X.
, отражающей возникающие бинарные отношения предпочтения и эквивалентности (или безразличия) на данном множестве X.
В том случае, если сравнение выявляет лишь факт предпочтения одной альтернативы над другой, результаты такого сравнения представляются не взвешенным ориентированным графом G = <V, U>, где V - множество вершин графа. Каждая вершина vi соответствует одной альтернативе xi. Множество дуг U ориентировано таким образом, чтобы определить предпочтение альтернатив. Если вариант xi > xj , то в графе существует дуга (i, j), направленная от вершины i к вершине j.
Тогдаэлементы матрицыаij определяются следующим образом
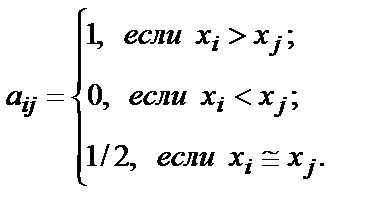
Диагональные элементы при этом обычно не фиксируются и могут быть любыми, но нередко дополнительно оговаривается, что аii =1/2. Таким образом, аij является индикатором факта превосходства одного элемента над другим или их равноценности (несравнимости).
Симметричные элементы аij и аji должны выбиратьсяравными, если соответствующие объекты равноценны или несравнимы.
Если результат сравнения отражает не только факт,но истепень превосходства, то каждая дуга ориентированного графа взвешена соответствующим числом аij.
Существуют следующие способы взвешивания отношений доминирования:
1. Турнирная калибровка (Т): аij ³ 0; аij + аji = с,
где аij - интерпретируется как число очков, набранных i-м игроком при его встречах с j-м игроком при общем числе встреч равных с.
2. Степенная калибровка (С): аij ³ 0; аij × аji = 1.
Здесь аij показывает, во сколько раз альтернатива xi превосходит альтернативу xj.
3. Кососимметричная калибровка (К): аij + аji = 0.
Данная калибровка показывает, на сколько один объект превосходит другой.
4. Вероятностная калибровка (В): аij Î[0, 1]; аij + аji = 1.
Значение аij указывает на вероятность того, что i-й вариант превосходит j-й вариант.
Переход от одной калибровки к другой возможен не всегда, а лишь при выполнении дополнительных условий, так как при этом может быть потеряна важная информация.
На рисунке 3 приведен граф, показывающий пути перехода между этими калибровками. Здесь буквами ПС (простая структура) обозначено не взвешенное доминирование.
| ПС |
| К |
| С |
| Т |
| В |
Рис. 3. Возможные пути переходов между калибровками
Если множество альтернатив W конечно и между альтернативами установлено отношение порядка R, то можно задать вещественную функцию со значениями j (х) и j (у) на W, для которой, если х < у, то j (х) < j (у). Задание такой функции позволяет перейти от языка бинарных отношений к критериальному языку, взяв j в качестве оценки альтернативы по критерию. Модели, устанавливающие такой критерий на определенном линейном порядке, называются моделями линейного упорядочивания.
Используемые на практике модели линейного упорядочивания традиционно разделяются на две большие группы, различающиеся своим подходом к решению задач упорядочивания.
В моделях первой группы каждому альтернативному варианту xi присваивается определенный интегральный показатель j i, оценивающий итоги его сравнения с остальными альтернативами. Далее исходит их ранжирование в зависимости от значений этого показателя. Если сразу несколько альтернатив имеют одинаковые показатели, то дляих упорядочивания используются дополнительные факторы, либо допускается произвольное упорядочивание таких альтернатив.
В моделях второй группы оцениваются показатели не отдельных альтернатив, а всего множества Х в целом и выбирается такое упорядочивание, которое оптимизирует некоторый функционал качества.
Рассмотрим некоторые разновидности моделей линейного упорядочивания для этих двух групп.
К первой группе относятся модели "спортивного" типа, модель Брэдли - Терри, модель Берджа, модель Ушакова и модель равномерного сглаживания.
В качестве примера модели второй группы будет приведена модель максимального согласования.
Дата добавления: 2018-06-28; просмотров: 501;
