Розыгрыш случайной вершины с заданным законом распределения.

Розыгрыш значений для дискретной случайной вершины аналогичен розыгрышу группы несовместных событий, если в качестве события А_i принять факт, что случайная вершина Х приняла значение, равное х_i.

Остановимся более подробно на розыгрыше случайной величины Х (непрерывной) с заданным законом распределения f(x).

Существуют различные способы генерации. Все они в качестве основы используют последовательность чисел R, распределённых равномерно на интервале [0, 1].

Рассмотрим один из этих способов – метод обратной функции:

Пусть необходимо сгенерировать случайную вершину Х, имеющую функцию плотности распределения f(x). Найдём для неё функцию распределения:

x

F(x) = ò f(x) dx

- ¥

По функции распределения вида y = F(x) найдём обратную ей функцию:

x=y(y)=F^-1(y)

Разыграем случайную вершину R=r и подставим это значение в обратную функцию y. Тогда найденное значение X = y(r) = F^-1(r) будет подчинено заданному закону распределения f(x), F(x).

Пример 1. Получение случайной величины Х, равномерно распределенной в интервале [A, B].

Запишем выражение для f(x) и F(x)

f(x) F(x)

1

A B x А В х

f(x) = 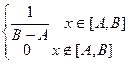F(x) =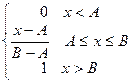

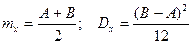
Найдем функцию y, обратную функции распределения F(x).

X= y(y) = F^-1(y) = y*(B-A)+A; X = R(B-A)+A

Сгенерировав значение R=r (например, r=0,6) и подставив его значение в X=y(r), получим соответствующее значение х, распределенное по закону f(x).

Пример 2. Получение случайной величины Х, распределенной по экспоненциальному закону распределения.

F(x)

l f(x)

1

x x

f(x) = l* e ^{-l x} , x³ 0 F(x) = 1 - e ^{-l x} , x ³ 0

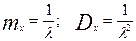
Обратная функция y будет.

Y= 1-e ^{-l x}

X= y(y) = (- 1/l)*ln(1-y), x= (- 1/l)*ln(1-R)

Поставив вместо у случайную величину R=r, получим Х, распределенный по экспоненциальному закону.

Обычно способ генерации указывается в справочниках по теории вероятности конкретно для каждого распределения.

Рассмотрим отдельно способ генерации случайной величины Х, распределённой по нормальному закону с параметрами m_X и D_X.

Генерировать её по методу обратной функции нецелесообразно, т.к. аналитического выражения не существует уже и для самой функции d(х). Обычно для генерации нормальной последовательности используют предельные свойства нормального закона распределения как сумму бесконечного числа одинаково распределённых случайных величин. При этом в качестве одинаково распределённых слагаемых используют равномерно распределённую случайную величину R, а число слагаемых на практике принимают равное 12.

Тогда получаем:

12

Y = S r_i

i=1

Где Y – нормально распределённая случайная величина с m_Y=12*(1/2)=6 и D_Y=12*(1/12)=1

Чтобы получить случайную величину Х с заданными параметрами m_X и s_X величину Y преобразуют по формуле:

X = m_X + s_X(Y–6) = m_X + s_X ( S r_i – 6).

i=1

Однако указанный метод требует генерации 12 равномерно распределённых случайных чисел для получения одного выбранного значения, что нецелесообразно при больших объёмах экспертов.

Существуют и другие способы генерации, позволяющие преодолеть указанную трудность.