Как в мат.статистике по множеству реализаций СВ!!!!!

В случае, если с помощью имитационного моделирования исследуются детерминированные процессы, то в качестве результатов используются значения переменных состояния, входящих в выбранный критерий эффективности, по которому оценивается качество работы исследуемой системы и вычисляемых с помощью модели. Очевидно, что результаты счета зависят при этом только от значения переменных, структуры и параметров самой модели и не меняются от прогона к прогону при одних и тех же исходных данных.

Адекватность модели исследуемым процессам может быть оценена по относительной погрешности между значениями показателя W_м , вычисленного с помощью модели и W_с полученного для реальной системы, если они могут быть получены в отдельных точках.

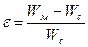или по S² =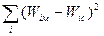

Если возможности получения значений W_c даже в отдельных точках не существует, то выводы об адекватности модели могут основываться на степени ее детализации и соответствия реальным процессам и на корректности использования математического аппарата.

В случае стохастического имитационного моделирования с использованием метода Монте-Карло производится N прогонов модели с розыгрышем всех случайных событий и величин, используемых в модели. В результате получаем N случайных реализаций процессов, оплачиваемых с помощью модели. На их основе могут быть найдены статистические оценки исследуемых показателей, такие как мат. ожидания.

,

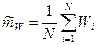где W_i – значение показателя в i-й реализации при некоторых фиксированных значениях переменной .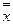

Дисперсии

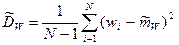
и пр., а также соответствующие им доверительные интервалы

для м.о.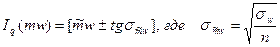

I_b= [w_min , w_max],

Величина которых при заданном уровне доверительной вероятности b зависит от числа реализации и оценки дисперсии самого показателя.

Для сокращения величины интервала кроме увеличения числа экспериментов, что не всегда возможно из-за значительного подчас времени счета одной реализации, используют специальные методы понижения дисперсии, проводя зависимые эксперименты с моделью.

Например: разыгрывая в одной реализации случайное событие А по значению случайной величины R (равномерно распределенной на [0,1]), а в другой – по значению (1-R) для одного и того же стартового числа ДСЧ. Или проводя дополнительные эксперименты с еще одной, менее детальной моделью, и используя согласованность их результатов.

Проверка адекватности модели в случае, если существует возможность наблюдения за реальной системой может быть осуществлена как по средним значениям, аналогично детерминированным моделям, так и по согласованности характеристик рассеивания модели и реальной системы по наблюдениям в различных точках. Например, с помощью Критерия Фишера.

Для этого проводится m независимых наблюдений над реальной системой в одной из точек 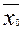значений входных переменных 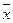и по полученным результатам ищется дисперсия воспроизводимости, характеризующая ошибки наблюдения

,

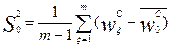где 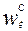- случайное значение показателя W в x-м наблюдении за реальной системой.

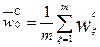- среднее значение показателя в точке .

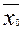Величина 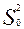характеризует разброс значений W в точке х₀ за счет случайных факторов. При этом предполагаем, что разброс значений показателя W во всей области наблюдения за системой 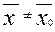за счет случайных факторов будет отличаться от 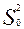незначительно.

Затем производятся N наблюдений за системой и моделирование с помощью модели при различных значениях входных переменных 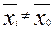. По полученным результатам определяется дисперсия адекватности.

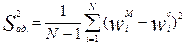
здесь: w_i^M, w_i^c – значения показателя w, найденные на модели и реальной системе в соответствующих точках .

По значениям 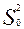и и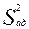щется дисперсионное отклонение.

F=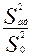

и соответствующее заданному уровню значимости q, числу степеней свободы r_ад=N-1 и r₀= m-1 критическое значение F_кр. Если вычисленное F<F_кр, то модель считается адекватной.

Величину F_кр ищут из таблиц F-распределения (часто путают распределение Фишера).

Если наблюдения за реальной системой или ее аналогами невозможен, то вывод об адекватности модели, как и для детерминированного случая может быть сделан только на основе анализа самой модели (эквивалентность логики функционирования, детальность учета существенных факторов, корректность применяемого мат. аппарата и т.д.)