Элементарные логические функции
Алгебра логики (булева алгебра)
· Первый закон обычной алгебры.
Коммутативный (переместительный) закон:
Х1+Х2=Х2+Х1;
Х1.Х2=Х2.Х1.
· Второй закон обычной алгебры.
Ассоциативный (сочетательный) закон:
Х1+(Х2+Х3)= (Х1+Х2)+Х3;
Х1.(Х2.Х3) = (Х1.Х2).Х3.
· Третий закон булевой алгебры.
Дистрибутивный (распределительный) закон:
(Х1+Х2).(Х1+Х2)= Х1+Х2.Х3.
Аксиомы формальной логики
1.  Х1+Х1=1;
Х1+Х1=1;
2. Х1.Х1=0;
3. Х2+Х2.Х3=Х2(1+Х3)= Х2.
Правила формальной логики
· Правило склеивания:
Х1(Х1+ Х2)=Х1;
· Правило повторения:
Х1.Х1=Х1 Х1+Х1=Х1;
· Правило отрицания:
 Х1+Х1=1;
Х1+Х1=1;
·  Аксиома двойного отрицания:
Аксиома двойного отрицания:
(Х1)=Х1;
· Операции с постоянными:
Х1.1 = Х1;
Х1+1= 1;
 0 = 1;
0 = 1;
Х1.0 = 0;
 Х1+0 = Х1;
Х1+0 = Х1;
1= 0
Теорема Де Моргана
1.  Х1+Х2=Х1.Х2;
Х1+Х2=Х1.Х2;
2. Х1.Х2= Х1+Х2;
3. Х1+Х2+Х3=Х1.Х2.Х3.
Элементарные логические функции
· х1+х2 = у — дизъюнкция (логическое сложение):
·  х1.х2 = у — конъюнкция (логическое умножение):
х1.х2 = у — конъюнкция (логическое умножение):
·  у = f(х1) = х1 — инверсия (отрицание):
у = f(х1) = х1 — инверсия (отрицание):
 | |||
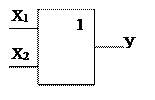 |
Таблица всевозможных функций двух переменных
| х1 | х2 | у0 | у1 | у2 | у3 | у4 | у5 | у6 | у7 | у8 | у9 | у10 | у11 | у12 | у13 | у14 | у15 |
у14 — логическое сложение;
у8 — логическое умножение;
инверсии нет;
у7 — логическая функция И-НЕ (штрих Шефера);
у1 — логическая функция ИЛИ-НЕ (стрелка Пирса);
у9 — операция эквивалентности (исключающее ИЛИ-НЕ);
у6 — операция неэквивалентности (исключающее ИЛИ; полусумматор по модулю 2).
В этой таблице представлены производные от основных логических функций.
Реализация функции эквивалентности в базисе И-ИЛИ-НЕ.
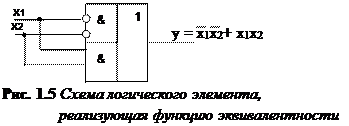 Таблица истинности такого логического элемента:
Таблица истинности такого логического элемента:
| х1 | x2 | y |
Реализация функции неэквивалентности в базисе И-ИЛИ-НЕ.
Таблица истинности такого логического элемента:
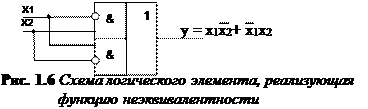 х1 х1
| x2 | y |
Дата добавления: 2018-03-01; просмотров: 1045;
