Задания для коллективного решения

Приложение интеграла к решению прикладных задач

Вычисление площади

Определённый интеграл 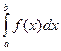непрерывной неотрицательной функции f(x) численно равенплощади криволинейной трапеции, ограниченной кривой y=f(x), осью О_х и прямыми х=а и х=b. В соответствии с этим формула площади записывается так:

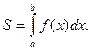
Рассмотрим некоторые примеры на вычисление площадей плоских фигур.

№ 1 Вычислить площадь, ограниченную линиями y=x²+1, y=0, x=0, x=2.

Решение. Построим фигуру, площадь которой мы должны будем вычислить.

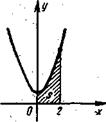y=x²+1 – это парабола ветви которой направлены вверх, и парабола смещена относительно оси O_y вверх на одну единицу (рисунок 1).

Рисунок 1. График функции y=x²+1

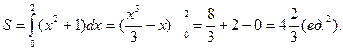
№ 2 Вычислить площадь, ограниченную линиями y=x²-1, y=0 в пределах от 0 до 1.

Решение. Графиком данной функции является парабола ветви, которой направлены вверх, и парабола смещена относительно оси O_y вниз на одну единицу (рисунок 2).

Рисунок 2. График функции y=x²-1

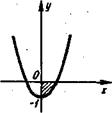
Имеем:

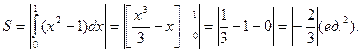
№ 3 Сделайте чертеж и вычислите площадь фигуры, ограниченной линиями y=8+2x----x² и y=2x-4.

Решение. Первая из двух данных линий – парабола, направленная ветвями вниз, поскольку коэффициент при x² отрицательный, а вторая линия – прямая, пересекающая обе оси координат.

Для построения параболы найдем координаты ее вершины: y’=2-2x; 2-2x=0, x=1 – абсцисса вершины; y(1)=8+2∙1-1²=9 – ее ордината, N(1;9) - вершина. Теперь найдем точки пересечения параболы и прямой, решив систему уравнений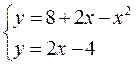

Приравнивая правые части уравнения, левые части которых равны, получим 8+2x-x²=2x-4 или x²-12=0, откуда .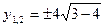

Итак, точки 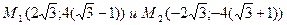- точки пересечения параболы и прямой (рисунок 1)

Рисунок 3 Графики функций y=8+2x-x² и y+2x-4

Построим прямую y=2x-4. Она проходит через точки (0;-4),(2;0) на осях координат. Для построения параболы можно еще ее точки пересечения с осью 0x, то есть корни уравнения 8+2x-x²=0 или x²-2x-8=0. По теореме Виета легко найти его корни: x₁=2, x₂=4. На рисунке3 изображена фигура (параболический сегмент M₁N M₂), ограниченный данными линиями

Вторая часть задачи состоит в нахождении площади этой фигуры. Ее площадь можно найти с помощью определенного интеграла по формуле .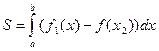

Применительно к данному условию, получим интеграл: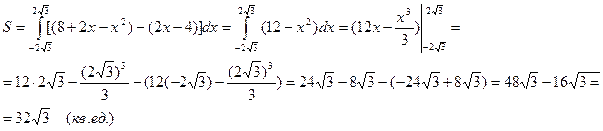

2 Вычисление объёма тела вращения

Объём тела, полученного от вращения кривой y=f(x) вокруг оси О_х, вычисляется по формуле:

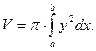
При вращении вокруг оси О_y формула имеет вид:

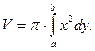
№ 4 Определить объём тела, полученного от вращения криволинейной трапеции, ограниченной прямыми х=0 х=3 и кривой y= 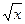вокруг оси О_х.

Решение. Построим рисунок (рисунок 4).

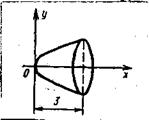
Рисунок 4. График функции y=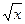

Искомый объём равен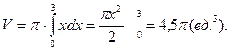

№ 5 Вычислить объём тела, полученного от вращения криволинейной трапеции, ограниченной кривой y=x² и прямыми y=0 и y=4 вокруг оси O_y.

Решение. Имеем:

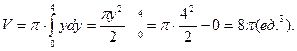
Задания для коллективного решения

1 Сделайте чертёж и вычислите площадь фигуры, ограниченной линиями:

1 y = 7x – x² – 6 и осью Ох.

2 у = 5 – x² и у = х + 3.

3 у = - 0, 5х² + 2 и у = 2 – х.

4 у = 6х – х² и у = 0.

5 у = х² –6х и осью Ох.

6 у = х² и у = 2х + 3.

7 у = х² + 1, х = 2 и осью Ох.

8 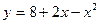и

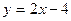
2 Вычислите объем тела, образованного вращением вокруг оси Оx фигуры, ограниченной данными линиями:

1 х · у = 8; х = 2; х = 8 ;у = 0.

2 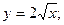x = 0: x = 9: y = 0.

3 у = 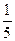х²; y = 0; x – 5 = 0; x = 0.

4 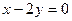; x = 0; x = 10; y = 0.

3 Сделайте чертёж и вычислите объём тела, образованного вращением вокруг оси Оy фигуры, ограниченной данными линиями:

1 y = x² + 1; y = 2; y = 5.

2 y = x³; y = 8; x = 0; y = 0.

3 x² – 2y = 0; y – 2 = 0.