Проверка гипотез о равенстве генеральных дисперсий двух нормально распределенных генеральных совокупностей.

Такая задача на практике возникает при необходимости сравнить точность двух приборов или методик исследования. Дисперсия характеризует разброс значений признака относительно генеральной средней. Чем меньше разброс результатов измерений, тем более точен прибор или метод.

Применяется F-критерий Фишера - Снедекора. В качестве критерия используется случайная величина 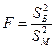, имеющая распределение Фишера – Снедекора (в случае истинности гипотезы 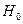). 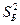- большая из исправленных выборочных дисперсий, а 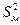- меньшая из исправленных выборочных дисперсий. Значение 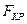находится по таблице критических точек распределения Фишера – Снедекора, зависит от уровня значимости 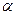и степеней свободы 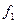и .

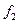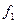· - это число степеней свободы той выборки, у которой больше исправленная выборочная дисперсия, .

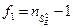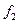· - это число степеней свободы той выборки, у которой исправленная выборочная дисперсия меньше, .

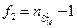Порядок проверки гипотезы:

1) выдвигаем гипотезы: ;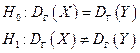

2) вычисляем наблюдаемое значение критерия: ;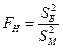

3) по таблице критических точек находим ;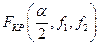

4) сравниваем 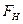и 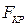(критерий двусторонний, но рассматривается как правосторонний).

Если 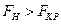, то нулевую гипотезу отвергаем, принимаем конкурирующую. Значит, генеральные дисперсии не равны, выборочные дисперсии различаются значимо.

Если 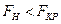, то нет оснований отвергать нулевую гипотезу. Значит, генеральные дисперсии равны, выборочные дисперсии различаются незначимо.

Если в исследовании необходимо доказать, что одна из дисперсий больше другой, то гипотезы выдвигаются следующим образом: 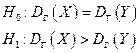. В этом случае значение 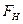вычисляется по той же формуле, 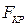находится также по таблице критических точек распределения Фишера – Снедекора, но зависит от 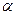, а не от 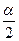( 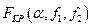). Выбор между гипотезам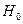и и 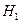осуществляется таким же образом, как в предыдущем случае.

Замечание: