Общие принципы проверки статистических гипотез

Полученные в результате эксперимента выборочные данные всегда ограничены и носят случайный характер. Они относятся к данной конкретной выборке, но могут служить основанием для суждения о генеральной совокупности. Одна из задач математической статистики состоит в переносе данных выборки на генеральную совокупность в целом. Однако, в силу случайных причин оценка параметров генеральной совокупности, сделанная на основе выборочных данных, всегда будет сопровождаться некоторой погрешностью. Поэтому оценки подобного рода должны рассматриваться как предположительные, а не как окончательные утверждения. Подобные предположения носят название статистических гипотез.

2.1. Статистические гипотезы, основные понятия.

Статистическая гипотеза – это предположение о виде неизвестного распределения или об его параметрах.

Например:

При проверке статистических гипотез всегда выдвигается две гипотезы:

· Нулевая(или основная) – гипотеза о сходстве, обозначается .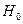

· Альтернативная (или конкурирующая) – гипотеза о различиях, обозначается .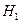

Цель проверки состоит в том, чтобы на основании выборочных данных принять решение о справедливости основной гипотезы или отклонить ее в пользу конкурирующей.

Для проверки основной гипотезы используется специально подобранная случайная величина К, которая должна удовлетворять определенным требованиям: 1) она должна являться функцией выборочных данных; 2) характеризовать меру расхождения выборочных данных с основной гипотезой; 3) ее закон распределения в случае истинности гипотезы 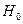должен быть известен. Случайная величина К называется статистическим критерием.

Наблюдаемое значение критерия ( 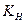) – это значение критерия, вычисленное по выборке, то есть зависящее от выборочных значений.

Допустимая область ( 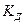) – это область значений критерия, которые не противоречат нулевой гипотезе.

Критическая область ( 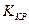) – это область значений критерия, при которых отвергается 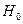и принимается .

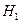Критические точки ( 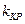) – это точки, отделяющие критическую область от допустимой.

Возможны три случая взаимного расположения критической и допустимой областей:

1) правосторонняя критическая область

2) левосторонняя критическая область

3) двусторонняя критическая область

Основной принцип принятия решения при проверкее статистических гипотез состоит в следующем: гипотеза 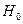отвергается, если значение 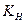, рассчитанное по выборке, принадлежит критической области, и не отвергается, если 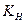принадлежит допустимой области.

В процедуре проверки статистической гипотезы можно выделить следующие этапы:

Этап 1. Выдвигаются нулевая и конкурирующая гипотезы ( 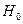и ).

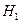Этап 2. Вычисляется наблюдаемое значение критерия.

Этап 3. По таблице находятся критические точки.

Этап 4.В зависимости от соотношения 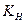и 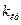выбирается одна из гипотез.

В результате проверки статистических гипотез возможны четыре случая:

Первый и третий случаи означают правильное решение. Во втором случае (гипотеза 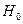верна, но отвергается) говорят, что совершается статистическая ошибка I рода. Вероятность статистической ошибки I рода обозначают 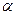и называют уровнем значимости. В биологических и медицинских исследованиях ее принимают равной 0,01 или 0,05.

В четвертом случае (гипотеза 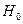не верна, но не отвергается) говорят, что совершается статистическая ошибка II рода. Вероятность статистической ошибки II рода обозначают 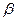. Величина 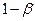называется мощностью критерия. Мощность критерия – это способность выявлять различия или отклонять гипотезу 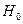, если она не верна.

В медицинских исследованиях можно решать экспериментальные задачи с использованием разных статистических критериев. При этом возможна такая ситуация, что один критерий позволяет обнаружить различия, а другой различий не выявляет. Это означает, что первый критерий является более мощным, чем второй. В таком случае возникает вопрос: зачем используют менее мощные критерии? Дело в том, что чем мощнее критерий, тем более трудоемка процедура его использования. Более того, если менее мощный критерий выявляет различия, то более мощный критерий подтвердит факт этих различий. Следовательно, использование менее мощных критериев является оправданным. Однако нельзя забывать о том, что отсутствие статистически значимых различий, зафиксированное с помощью какого-либо критерия, не является гарантией того, что более мощный критерий их не выявит.

Виды критериев

Прежде, чем выполнить любой эксперимент, необходимо:

· четко сформулировать его задачи;

· определить экспериментальную гипотезу;

· выбрать соответствующий статистический метод, наиболее эффективный для решения поставленных в исследовании задач.

Подавляющее большинство задач, решаемых в медицинских и биологических экспериментах, предполагает те или иные сопоставления. Такой тип эксперимента называется сравнительным. Причем, можно сравнивать два эмпирических распределения между собой или эмпирическое распределение с теоретическим.

При решении первого типа задач необходимо знать следующее:

· Тип организации эксперимента – являются выборки зависимыми или независимыми.

ü Выборки называются независимыми(или несвязными), если процедура эксперимента и результаты измерения, полученные на одной из выборок, не оказывают влияния на особенности протекания эксперимента и результаты измерения у другой выборки.

ü Выборки называются зависимыми(или связными), если процедура эксперимента и результаты измерения, полученные на одной выборке, оказывают влияние на особенности протекания эксперимента и результаты измерения у другой выборки.

Использование зависимых выборок позволяет снизить влияние случайных причин и сгладить индивидуальные различия между исследуемыми объектами.

· Вид закона распределения исследуемой случайной величины. Знание закона распределения позволяет сделать выбор между параметрическими и непараметрическими критериями.

ü Параметрические критерии основаны на конкретном виде распределения изучаемой случайной величины (как правило, на нормальном распределении) и используют числовые характеристики выборочной совокупности (выборочную среднюю, выборочную дисперсию и т.п.), которые являются точечными оценками параметров генеральной совокупности.

ü Непараметрические критерии не базируются на предположении о виде распределения изучаемой величины и используют непосредственно выборочные данные, а не параметры выборки.

Если изучаемая величина распределена нормально, то отдают предпочтение параметрическим критериям, так как они обладают большей мощностью. Но как показывает практика, подавляющее большое данных в медицинских исследованиях не имеет нормального распределения, поэтому часто применяются критерии непараметрические.

Если в результате исследования возникает предположение, что изучаемая величина может иметь нормальное распределение, то это предположение необходимо проверить. Для этого используются так называемые критерии согласия.