Понятие об интерполяции и экстраполяции. Сезонные колебания

Приближенный расчет уровней, лежащих внутри ряда динамики, но почему-либо неизвестных, называется интерполяцией. Такой расчет проводится на основе данных фактически сложившихся (реальных) уровней ряда на уже сложившемся определенном промежутке времени. Например, метод аналитического выравнивания уровней ряда динамики с той или иной степенью адекватности позволяет построить аппроксимацию (приближение) основной тенденции развития ряда динамики в виде аналитической функции y(t), дающей значения неизвестных уровней, лежащих внутри этого ряда. В этом случае интерполяция есть расчет неизвестных уровней с помощью адекватной математической функции фактически сложившегося ряда динамики, описывающего социально-экономическое явление.

Однако, основной целью анализа динамических рядов является не столько описание математическими методами и приёмами уже свершившейся динамики явлений, сколько получение на основе имеющихся данных научного анализа возможного развития явления в будущем.

Составление надёжных прогнозов динамики социальной и экономической деятельности является необходимым условием устойчивости регулирования социальных и рыночных отношений. Огромное значение при этом принадлежит методу экстраполяции.

Под экстраполяциейпонимается распространение выявленных в анализе рядов динамики закономерностей развития изучаемого явления на будущее. Другими словами, экстраполяция есть продление в будущее тенденции, наблюдающейся в прошлом.

Выводы по тенденции развития социально-экономических явлений, получаемые на основе экстраполяции называют прогнозированием. Основой прогнозирования является предположение, что закономерность, действующая внутри анализируемого ряда динамики, выступающего в качестве базы прогнозирования, сохраняется и в дальнейшем.

Возможность экстраполяции обеспечивается двумя обстоятельствами:

1) общие условия, определяющие тенденцию развития в прошлом, не претерпевают

существенных изменений в будущем;

2) тенденция развития явления характеризуется тем или иным аналитическим

уравнением.

Большое значение при экстраполяции имеет продолжительность базисного ряда динамики и сроков прогнозирования. Установление сроков прогнозирования зависит от задачи исследования, однако, следует иметь в виду, что чем короче сроки прогноза, тем надёжнее результаты экстраполяции.

Рассмотрим пример. Среднегодовой объём реализации телевизоров в районе в 2003г. составил 6820 шт. Анализ базового ряда динамики показал, что абсолютные приросты за несколько предыдущих лет стабильны и равны 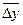= 240 шт. Необходимо произвести прогноз объёма реализации в 2004г. Поскольку тенденция развития в этом случае имеет прямо пропорциональный характер, то

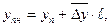
где 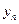= 6820 шт.; 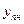– прогнозируемый уровень в 2004г.; 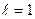год – срок прогноза. В результате расчёта получим

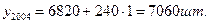
Одной из основных задач анализа рядов динамики является выявление сезонных колебаний уровней социально-экономических явлений.

Под сезонными колебаниямипонимаются более или менее устойчивые внутригодовые колебания уровней развития социально-экономических явлений. Проявляются они во всех сферах жизни общества: производстве, обращении, потреблении. Поэтому статистическое изучение сезонных колебаний имеет большое практическое значение.

В условиях периодической сменяемости сезонов жизнедеятельность людей сопровождается изменениями интенсивности динамики социально-экономических процессов. В большинстве отраслей экономики это проявляется в виде внутригодовых чередований подъёмов и спадов выпуска продукции, неодинаковом потреблении сырья и энергии, колебании уровней производительности труда, себестоимости, прибыли и других показателей. Для некоторых сфер деятельности внутригодовая динамика характеризуется приостановкой процессов в межсезонные периоды (сельское хозяйство, рыболовство, охота, навигация, туризм и т.д.). Значительной колеблемости во внутригодовой динамике подвержены денежное обращение и товарооборот.

Статистические ряды внутригодовой динамики обычно составляются по материалам текущей отчётности. Разновеликие по продолжительности месяцы и кварталы годовых периодов являются одной из причин, влияющих на изменения уровней рядов внутригодовой динамики, поэтому основные требования построения и приведения рядов динамики к сопоставимому виду (раздел 7.1) является одним из непременных условий изучения сезонных колебаний. Часто для устранения влияния разновеликости периодов объёмные величины пересчитываются в средние величины, характеризующие интенсивность развития явления в единицу времени, и это имеет существенное значение для повышения точности показателей сезонных колебаний.

Для измерения сезонных колебаний обычно исчисляются индексы сезонности i_s . В общем виде они определяются отношением исходных (фактических) уровней ряда динамики 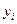к теоретическим (расчётным) уровням 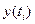, выступающим в качестве базы сравнения:

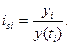
В результате того, что измерение сезонных колебаний проводится на базе соответствующих теоретических уровней тренда 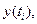в индивидуальных индексах сезонности 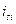влияние основной тенденции развития устраняется (элиминируется).

Для каждого периода годового цикла определяются обобщённые показатели в виде средних индексов сезонности:

.

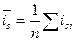Для рядов внутригодовой динамики, в которых тренд отсутствует или незначителен, последняя формула приобретает вид:

,

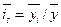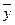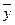где _i , - средний уровень показателя отдельного внутригодового периода и среднегодовое значение уровня, соответственно.