Социально-экономических явлений

Применение методов укрупнения интервалов и сглаживания скользящих средних позволяет выявить тренд ряда динамики, но измерить тренд и получить статистическую оценку его адекватности посредством этих методов невозможно. Такую задачу решают с помощью метода аналитического выравнивания.

Метод аналитического выравниваниясостоит в том, что основная тенденция развития ряда динамики с уровнями 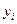рассчитывается как теоретическая функция времени 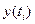таким образом, что эта функция наилучшим образом отображает основную тенденцию ряда динамики. Такую функцию называют адекватной математической функцией.

В качестве критерия и метода оценки соответствия (адекватности) между теоретическими 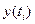и эмпирическими 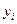уровнями выступает метод наименьших квадратов,состоящий в том, что сумма квадратов отклонений теоретических значений уровня от эмпирических должна быть минимальной. Математически метод наименьших квадратов представляется уравнением

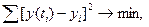
которое является необходимым математическим условием подбора адекватной функции, рассчитанные (теоретические) значения которой максимально соответствуют фактическим (эмпирическим) уровням ряда динамики.

Важнейшей проблемой в применении метода аналитического выравнивания является подбор математической функции, по которой рассчитываются теоретические уровни тренда. От правильности её решения зависят выводы о закономерностях тренда изучаемого явления. Если выбранный тип аналитической функции адекватен основной тенденции развития изучаемого явления во времени, то полученная на этой основе трендовая модель будет иметь полезное применение при изучении сезонных колебаний, прогнозировании и других практических целях.

Одним из условий обоснованного применения метода аналитического выравнивания в анализе рядов динамики является знание типов развития социально-экономических явлений во времени, их основных отличительных признаков.

В практике статистического изучения тренда различают следующие эталонные типы развития явлений во времени:

1) равномерное развитие. Для этого типа динамики присущи постоянные абсолютные приросты:

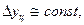
а основной тренд в рядах динамики со стабильными приростами отображается уравнением прямолинейной функции

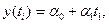
где 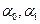- параметры уравнения; 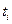- время. При 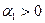уровни ряда динамики равномерно возрастают, а при 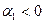происходит их равномерное снижение;

2) равноускоренное (равнозамедленное) развитие. Этому типу динамики присуще

изменение уровней ряда с постоянными темпами прироста:

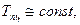
а основной тренд в рядах динамики со стабильными темпами прироста отображается функцией параболы второго порядка

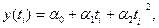
где параметр 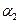характеризует изменение интенсивности развития в единицу времени (ускорение). При 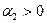происходит ускорение развития, а при 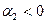идёт процесс замедления роста;

3) развитие с переменным ускорением. Для этого типа динамики основной тренд

выражается функцией параболы третьего порядка

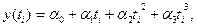
где параметр 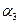отображает изменение ускорения. При 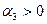ускорение возрастает, а при 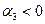ускорение замедляется;

4) развитие по экспоненте. Этот тип динамики характеризуется темпами роста

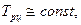
а основная тенденция рядов динамики с постоянными темпами роста отображается показательной функцией

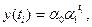
где 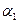- темп роста (снижения) изучаемого явления в единицу времени, т.е. интенсивность развития;

5) развитие с замедлением роста в конце периода. У этого типа динамики цепной абсолютный прирост уменьшается по величине в конечном числе уровней ряда динамики

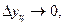
а основная тенденция развития в таких рядах динамики выражается полулогарифмической функцией

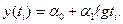
При аналитическом выравнивании рядов динамики можно применять и другие математические функции (например, степенная функция, функция гиперболы и т.д.). Специфика и основные свойства математических функций рассматриваются в дисциплинах по экономико-математическим методам.

Практика статистического изучения тренда с использованием средств современной вычислительной техники показывает, что в решении выбора адекватной математической функции определяющее значение имеет обеспеченность исследователя пакетом стандартных программ для машинной обработки исходной информации. Быстродействие (мощность) современных ЭВМ позволяет получать все необходимые для анализа тренда показатели, в том числе и применяемые для выбора адекватной математической функции.

Одним из наиболее часто применяемых в практике показателей адекватности математической функции является стандартизованная ошибка аппроксимации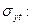

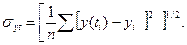
Применение последней формулы в изучении тренда основано на том, что за наиболее адекватную принимается формула, у которой стандартизованная ошибка аппроксимации минимальная.