Расчет на продавливание элемента с поперечной арматурой 1 страница
3.86. Расчет элементов с поперечной арматурой на продавливание при действии сосредоточенной силы (черт. 3.48) производят из условия
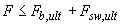 , (3.184)
, (3.184)
где 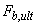 - правая часть условия (3.177);
- правая часть условия (3.177);
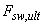 - предельное усилие, воспринимаемое поперечной арматурой при продавливании и равное
- предельное усилие, воспринимаемое поперечной арматурой при продавливании и равное
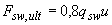 , (3.185)
, (3.185)
но принимаемое не более 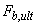 ,
,
где 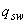 - усилие в поперечной арматуре на единицу длины контура расчетного поперечного сечения, равное при равномерном распределении поперечной арматуры
- усилие в поперечной арматуре на единицу длины контура расчетного поперечного сечения, равное при равномерном распределении поперечной арматуры
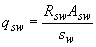 , (3.186)
, (3.186)
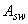 - площадь сечения поперечной арматуры с шагом
- площадь сечения поперечной арматуры с шагом 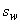 , расположенная в пределах расстояния
, расположенная в пределах расстояния 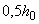 по обе стороны от контура расчетного поперечного сечения (см. черт.3.48)
по обе стороны от контура расчетного поперечного сечения (см. черт.3.48)
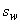 - шаг поперечных стержней в направлении контура поперечного сечения.
- шаг поперечных стержней в направлении контура поперечного сечения.
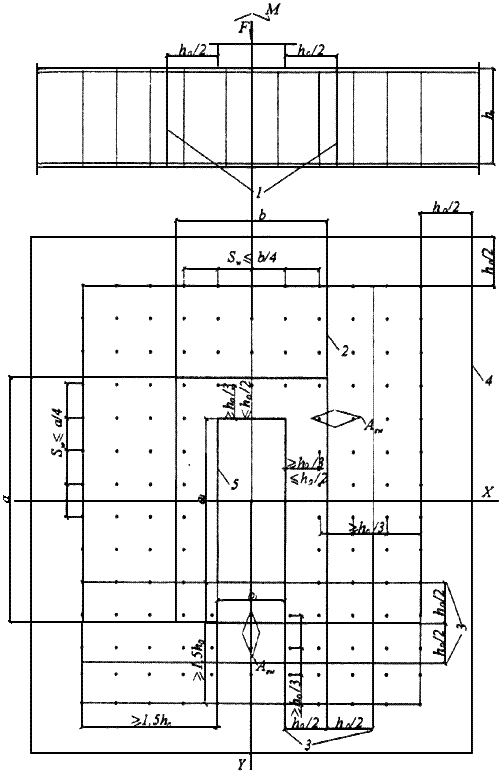
Черт.3.48 Схема для расчета железобетонных плит с вертикальной равномерно распределенной поперечной арматурой на продавливание
1 - расчетное поперечное сечение; 2 - контур расчетного поперечного сечения; 3 - границы зоны, в пределах которых в расчете учитывается поперечная арматура; 4 - контур расчетного поперечного сечения без учета в расчете поперечной арматуры;
5 - контур площадки приложения нагрузки.
При равномерном расположении поперечной арматуры вдоль контура расчетного поперечного сечения значение 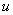 принимается как для бетонного расчетного поперечного сечения согласно п.3.84.
принимается как для бетонного расчетного поперечного сечения согласно п.3.84.
При расположении поперечной арматуры сосредоточенно у осей площадки опирания (крестообразное расположение поперечной арматуры, черт.3.49) периметр контура 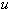 для поперечной арматуры принимают по фактическим длинам участка расположения поперечной арматуры
для поперечной арматуры принимают по фактическим длинам участка расположения поперечной арматуры 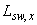 и
и 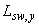 на расчетном контуре продавливания [т.е.
на расчетном контуре продавливания [т.е. 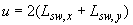 ].
].
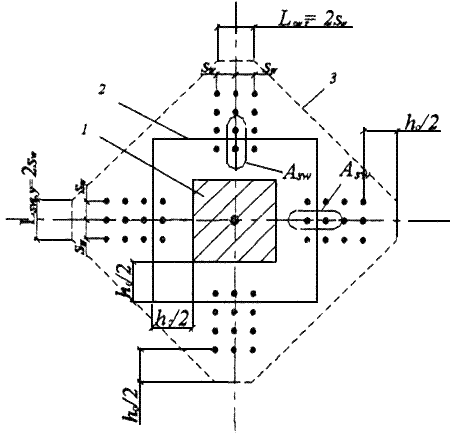
Черт.3.49. Схема расчетного контура поперечного сечения при продавливании и при крестообразном расположении поперечной арматуры
1 - площадь приложения нагрузки; 2 - контур расчетного поперечного сечения при учете поперечного армирования 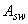 ;
;
3 - контур расчетного поперечного сечения без учета поперечного армирования
Поперечную арматуру учитывают в расчете при 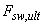 не менее
не менее 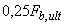 .
.
За границей расположения поперечной арматуры расчет на продавливание производят согласно п.3.48, рассматривая контур расчетного поперечного сечения на расстоянии 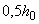 от границы расположения поперечной арматуры.
от границы расположения поперечной арматуры.
При сосредоточенном расположении поперечной арматуры по осям площадки опирания, кроме того, расчетный контур поперечного сечения бетона принимают по диагональным линиям, следующим от края расположения поперечной арматуры (см. черт.3.49).
Поперечная арматура должна удовлетворять конструктивным требованиям, приведенным в п.5.26.
3.87. Расчет элементов с поперечной арматурой на продавливание при совместном действии сосредоточенных силы и изгибающего момента (см. черт.3.48) производят из условия
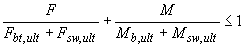 , (3.187)
, (3.187)
где отношение 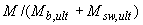 принимается не
принимается не 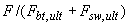 ;
;
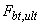 и
и 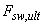 - см. п.3.86;
- см. п.3.86;
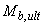 - предельный сосредоточенный момент, воспринимаемый бетоном в расчетном поперечном сечении и равный
- предельный сосредоточенный момент, воспринимаемый бетоном в расчетном поперечном сечении и равный
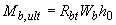
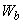 - см. п.3.85;
- см. п.3.85;
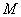 - см. п.3.85;
- см. п.3.85;
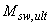 - предельный сосредоточенный момент, воспринимаемый поперечной арматурой в расчетном поперечном сечении и равный
- предельный сосредоточенный момент, воспринимаемый поперечной арматурой в расчетном поперечном сечении и равный
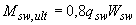 ;
;
но принимаемый не более 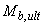 ;
;
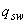 - см. п.3.86;
- см. п.3.86;
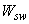 - момент сопротивления контура поперечной арматуры.
- момент сопротивления контура поперечной арматуры.
При равномерном расположении поперечной арматуры вдоль контура расчетного поперечного сечения значение 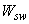 принимается равным
принимается равным 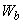 .
.
При расположении поперечной арматуры сосредоточенно у осей площадки опирания (черт.3.49) момент сопротивления 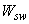 определяют по тем же правилам, что и момент сопротивления,
определяют по тем же правилам, что и момент сопротивления, 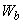 , принимая фактические длины участков расположения поперечной арматуры
, принимая фактические длины участков расположения поперечной арматуры 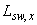 и
и 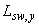 на расчетном контуре продавливания.
на расчетном контуре продавливания.
При равномерном расположении поперечной арматуры вокруг площади опирания вместо условия (3.187) можно воспользоваться условием (3.182) с увеличением правой части на величину 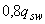 , принимаемой не более
, принимаемой не более 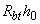 .
.
При действии добавочного момента 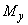 в направлении, нормальном направлению момента
в направлении, нормальном направлению момента 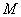 , левая часть условия (3.187) увеличивается на
, левая часть условия (3.187) увеличивается на 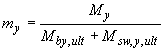 , где
, где 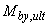 и
и 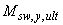 - предельные сосредоточенные моменты, воспринимаемые соответственно бетоном и поперечной арматурой в расчетном поперечном сечении в направлении действия момента
- предельные сосредоточенные моменты, воспринимаемые соответственно бетоном и поперечной арматурой в расчетном поперечном сечении в направлении действия момента 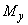 ; при этом сумма
; при этом сумма 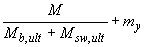 , также принимается не более
, также принимается не более 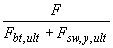 , а
, а 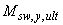 не более
не более 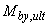 .
.
Примеры расчета
Пример 40. Дано: плита плоского монолитного перекрытия толщиной 220 мм; колонны, примыкающие к перекрытию сверху и снизу, сечением 500x800 мм; нагрузка, передающаяся с перекрытия на колонну 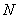 =800 кН; моменты в сечениях колонн по верхней и по нижней граням плиты равны: в направлении размера колонны 500 мм -
=800 кН; моменты в сечениях колонн по верхней и по нижней граням плиты равны: в направлении размера колонны 500 мм - 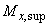 =70 кН·м,
=70 кН·м, 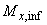 =60 кН·м, в направлении размера колонны 800 мм -
=60 кН·м, в направлении размера колонны 800 мм - 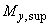 =30 кН·м,
=30 кН·м, 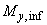 =27 кН·м; бетон класса В30 (
=27 кН·м; бетон класса В30 ( 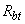 =1,15 МПа).
=1,15 МПа).
Требуется проверить плиту перекрытия на продавливание.
Расчет. Усредненную рабочую высоту плиты принимаем равной 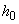 =190 мм.
=190 мм.
За сосредоточенную продавливающую силу принимаем нагрузку от перекрытия 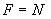 =800 кН; за площадь опирания этой силы - сечение колонны
=800 кН; за площадь опирания этой силы - сечение колонны 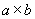 =500x800 мм.
=500x800 мм.
Определим геометрические характеристики контура расчетного поперечного сечения согласно пп.3.84 и 3.85:
периметр 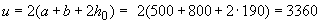 мм;
мм;
момент сопротивления в направлении момента  (т.е. при
(т.е. при 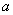 =500 мм,
=500 мм, 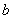 =800 мм)
=800 мм)
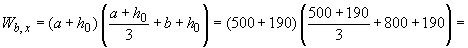
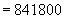 мм
мм  ;
;
момент сопротивления в направлении момента 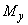 (т.е. при
(т.е. при 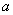 =800 мм,
=800 мм, 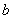 =500 мм)
=500 мм)
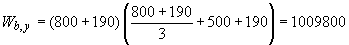 мм
мм  .
.
За расчетный сосредоточенный момент в каждом направлении принимаем половину суммы моментов в сечении по верхней и по нижней граням плиты, т.е.
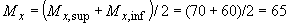 кН·м;
кН·м;
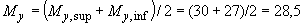 кН·м.
кН·м.
Проверяем условие (3.182), принимая 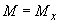 =65 кН·м,
=65 кН·м, 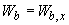 =841800 мм
=841800 мм  и добавляя к левой части
и добавляя к левой части 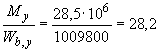 Н/мм.
Н/мм.
При этом 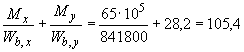 Н/мм
Н/мм 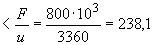 Н/мм, следовательно, момент не корректируем.
Н/мм, следовательно, момент не корректируем.
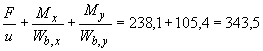 Н/мм
Н/мм 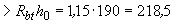 Н/мм,
Н/мм,
т.е. условие (3.182) не выполняется и необходимо установить в плите поперечную арматуру.
Принимаем согласно требованиям п.5.26 шаг поперечных стержней 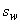 =60 мм
=60 мм 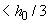 =63,3 мм, 1-й ряд стержней располагаем на расстоянии от колонны 75 мм, поскольку 75 мм
=63,3 мм, 1-й ряд стержней располагаем на расстоянии от колонны 75 мм, поскольку 75 мм 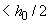 и 75 мм
и 75 мм 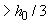 (черт.3.50). Тогда в пределах на расстоянии
(черт.3.50). Тогда в пределах на расстоянии 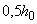 =95 мм по обе стороны от контура расчетного поперечного сечения может разместиться в одном сечении 2 стержня. Принимаем стержни из арматуры класса A240 (
=95 мм по обе стороны от контура расчетного поперечного сечения может разместиться в одном сечении 2 стержня. Принимаем стержни из арматуры класса A240 ( 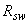 =170 МПа) минимального диаметра 6 мм.
=170 МПа) минимального диаметра 6 мм.
Тогда 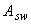 =57 мм
=57 мм  и
и 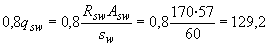 Н/мм
Н/мм 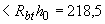 Н/мм.
Н/мм.
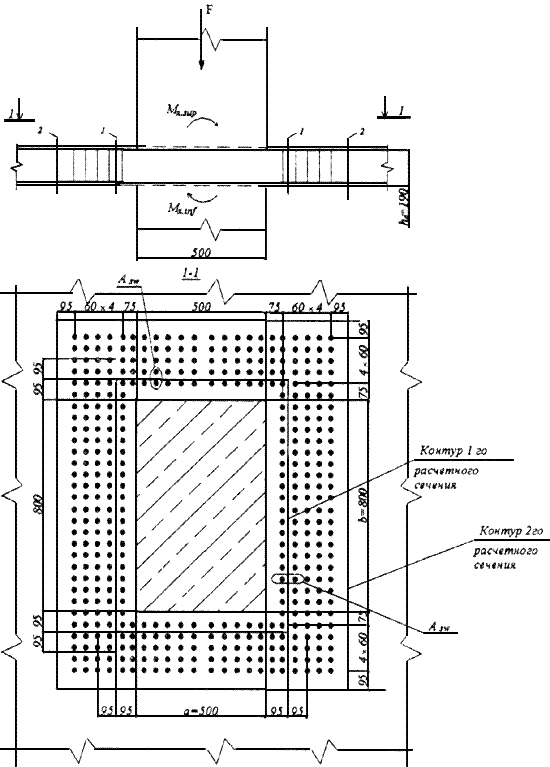
Черт.3.50. К примеру расчета 40
1 - 1-е расчетное сечение, 2 - 2-е расчетное сечение
При этом согласно п.3.86 предельное усилие, воспринимаемое поперечной арматурой и равное 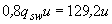 , должно быть неменее
, должно быть неменее 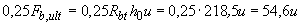 . Как видим, это требование выполнено.
. Как видим, это требование выполнено.
Проверяем условие (3.182) с добавлением к правой части значения 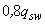
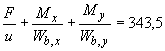 Н/мм
Н/мм 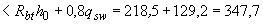 Н/мм, т.е. прочность расчетного сечения с учетом установленной поперечной арматуры обеспечена.
Н/мм, т.е. прочность расчетного сечения с учетом установленной поперечной арматуры обеспечена.
Проверяем прочность расчетного сечения с контуром на расстоянии 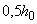 за границей расположения поперечной арматуры. Согласно требованиям п.5.26 последний ряд поперечных стержней располагается на расстоянии от грузовой площадки (т.е. от колонны), равном 75+4·60=315 мм
за границей расположения поперечной арматуры. Согласно требованиям п.5.26 последний ряд поперечных стержней располагается на расстоянии от грузовой площадки (т.е. от колонны), равном 75+4·60=315 мм 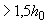 =1,5·190=285 мм. Тогда контур нового расчетного сечения имеет размеры:
=1,5·190=285 мм. Тогда контур нового расчетного сечения имеет размеры: 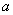 =500+2·315+190=1330 мм;
=500+2·315+190=1330 мм; 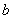 =800+2·315+190=1620 мм.
=800+2·315+190=1620 мм.
Его геометрические характеристики:
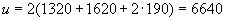 мм;
мм;
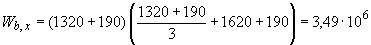 мм
мм  ;
;
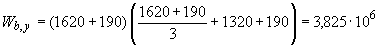 мм
мм  .
.
Проверяем условие (3.182) с учетом момента 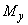 . При этом пренебрегаем "в запас" уменьшением продавливающей силы
. При этом пренебрегаем "в запас" уменьшением продавливающей силы 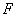 за счет нагрузки, расположенной на участке с размерами
за счет нагрузки, расположенной на участке с размерами 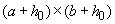 вокруг колонны.
вокруг колонны.
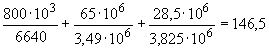 Н/мм
Н/мм 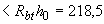 Н/мм,
Н/мм,
т.е. прочность этого сечения обеспечена.
Пример 41. Дано: плита плоского монолитного перекрытия толщиной 230 мм; колонны, примыкающие к перекрытию сверху и снизу, сечением 400х500 мм; нагрузка, передающаяся с перекрытия на колонну 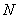 =150 кН; моменты в сечениях колонн по верхней и по нижней граням плиты в направлении размера колонны 500 мм -
=150 кН; моменты в сечениях колонн по верхней и по нижней граням плиты в направлении размера колонны 500 мм - 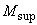 =80 кН·м,
=80 кН·м, 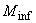 =90 кН·м; центр сечения колонны расположен на расстоянии
=90 кН·м; центр сечения колонны расположен на расстоянии 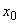 =500 мм от свободного края плиты (черт.3.51); бетон класса В25 (
=500 мм от свободного края плиты (черт.3.51); бетон класса В25 ( 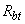 =1,05 МПа).
=1,05 МПа).
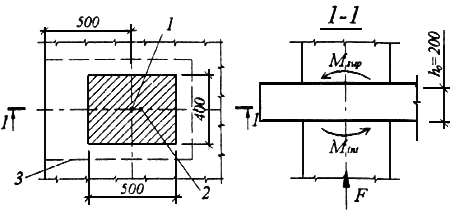
Черт.3.51. К примеру расчета 41
1 - точка приложения силы 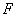 ; 2 - центр тяжести незамкнутого контура; 3 - незамкнутый контур расчетного сечения
; 2 - центр тяжести незамкнутого контура; 3 - незамкнутый контур расчетного сечения
Требуется проверить плиту перекрытия на продавливание.
Расчет. Усредненную рабочую высоту плиты принимаем равной 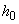 =200 мм.
=200 мм.
За сосредоточенную продавливающую силу 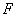 , направленную снизу вверх, принимаем нагрузку от перекрытия
, направленную снизу вверх, принимаем нагрузку от перекрытия 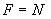 =150 кН; за площадь опирания этой силы - сечение колонны
=150 кН; за площадь опирания этой силы - сечение колонны 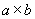 =500x400 мм.
=500x400 мм.
Проверим прочность расчетного сечения незамкнутого контура. Размеры этого контура равны:
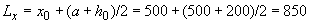 мм;
мм;
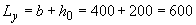 мм.
мм.
Периметр и момент инерции контура равны
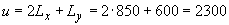 мм;
мм;
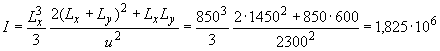 мм
мм 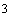 .
.
Эксцентриситет силы 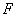
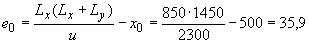 мм.
мм.
При принятых направлениях моментов 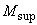 и
и 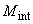 (см. черт.3.51) наиболее напряженное волокно расчетного сечения расположено по краю сечения, наиболее удаленному от свободного края плиты. Это волокно расположено на расстоянии от центра тяжести равном
(см. черт.3.51) наиболее напряженное волокно расчетного сечения расположено по краю сечения, наиболее удаленному от свободного края плиты. Это волокно расположено на расстоянии от центра тяжести равном 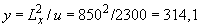 мм.
мм.
Тогда момент сопротивления равен:
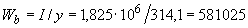 мм
мм  .
.
Расчетный момент от колонн равен
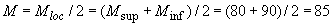 кН·м.
кН·м.
Момент от эксцентричного приложения силы 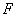 равен
равен 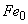 =150·0,0359=5,4 кН·м. Этот момент противоположен по знаку моменту
=150·0,0359=5,4 кН·м. Этот момент противоположен по знаку моменту 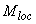 , следовательно
, следовательно
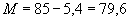 кН·м.
кН·м.
Проверяем прочность из условия (3.182)
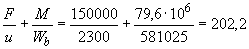 Н/мм
Н/мм 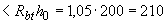 Н/мм, т.е. прочность сечения с незамкнутым контуром обеспечена.
Н/мм, т.е. прочность сечения с незамкнутым контуром обеспечена.
Проверим прочность сечения замкнутого контура. Определяем его геометрические характеристики:
Периметр 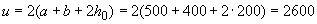 мм;
мм;
Момент сопротивления 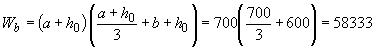 мм
мм  ;
;
Момент равен 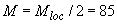 кН·м.
кН·м.
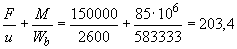 Н/мм
Н/мм 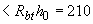 Н/мм, т.е. прочность плиты на продавливание обеспечена по всем сечениям.
Н/мм, т.е. прочность плиты на продавливание обеспечена по всем сечениям.
4. РАСЧЕТ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО РАСКРЫТИЮ ТРЕЩИН
ОБЩИЕ ПОЛОЖЕНИЯ
4.1. Расчет железобетонных элементов производят по непродолжительному раскрытию трещин и продолжительному раскрытию трещин.
Непродолжительное раскрытие трещин определяют от совместного действия постоянных и временных (длительных и кратковременных) нагрузок; продолжительные - только от постоянных и временных длительных нагрузок.
4.2. Расчет по раскрытию трещин производят из условия
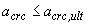 , (4.1)
, (4.1)
где 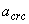 - ширина раскрытия трещин от действия внешней нагрузки, определяемая согласно пп.4.10-4.14;
- ширина раскрытия трещин от действия внешней нагрузки, определяемая согласно пп.4.10-4.14;
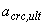 - предельно допустимая ширина раскрытия трещин.
- предельно допустимая ширина раскрытия трещин.
Значения 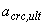 принимают равными:
принимают равными:
а) из условия сохранности арматуры (для любых конструкций)
0,3 мм - при продолжительном раскрытии трещин;
0,4 мм - при непродолжительном раскрытии трещин;
б) из условия ограничения проницаемости конструкций (для конструкций, подверженных непосредственному давлению жидкостей, газов, сыпучих тел)
0,2 мм - при продолжительном раскрытии трещин;
0,3 мм - при непродолжительном раскрытии трещин.
4.3. Расчет по раскрытию трещин не производится, если соблюдается условие
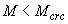 , (4.2)
, (4.2)
где 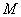 - момент от внешней нагрузки относительно оси, нормальной к плоскости действия момента и проходящей через центр тяжести приведенного поперечного сечения элемента; при этом учитываются все нагрузки (постоянные и временные) с коэффициентом надежности по нагрузке
- момент от внешней нагрузки относительно оси, нормальной к плоскости действия момента и проходящей через центр тяжести приведенного поперечного сечения элемента; при этом учитываются все нагрузки (постоянные и временные) с коэффициентом надежности по нагрузке 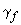 =1;
=1;
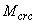 - момент, воспринимаемый нормальным сечением элемента при образовании трещин, определяемый согласно пп.4.4-4.8.
- момент, воспринимаемый нормальным сечением элемента при образовании трещин, определяемый согласно пп.4.4-4.8.
Для центрально растянутых элементов условие (4.2) преобразуется в условие
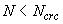 , (4.3)
, (4.3)
где 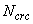 - продольное растягивающее усилие, воспринимаемое элементом при образовании трещин, определяемое согласно п.4.9
- продольное растягивающее усилие, воспринимаемое элементом при образовании трещин, определяемое согласно п.4.9
ОПРЕДЕЛЕНИЕ МОМЕНТА ОБРАЗОВАНИЯ ТРЕЩИН
4.4. Изгибающий момент 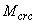 при образовании трещин определяется на основе деформационной модели с учетом неупругих деформаций растянутого бетона согласно пп.4.7 и 4.8.
при образовании трещин определяется на основе деформационной модели с учетом неупругих деформаций растянутого бетона согласно пп.4.7 и 4.8.
Допускается определять момент 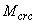 без учета неупругих деформаций бетона согласно пп.4.5 и 4.6. Если при этом условие (4.1) не удовлетворяется, то момент образования трещин следует определять с учетом неупругих деформаций бетона.
без учета неупругих деформаций бетона согласно пп.4.5 и 4.6. Если при этом условие (4.1) не удовлетворяется, то момент образования трещин следует определять с учетом неупругих деформаций бетона.
4.5. Момент образования трещин без учета неупругих деформаций бетона определяют как для сплошного упругого тела по формуле
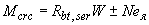 , (4.4)
, (4.4)
где 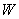 - момент сопротивления приведенного сечения для крайнего растянутого волокна бетона:
- момент сопротивления приведенного сечения для крайнего растянутого волокна бетона:
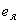 - расстояние от центра тяжести приведенного сечения элемента до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется.
- расстояние от центра тяжести приведенного сечения элемента до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется.
Значения 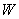 и
и 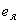 определяются согласно п.4.6.
определяются согласно п.4.6.
В формуле (4.4) знак "плюс" принимают при сжимающей продольной силе 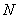 , знак "минус" - при растягивающей силе.
, знак "минус" - при растягивающей силе.
4.6. Момент сопротивления 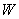 и расстояние
и расстояние 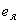 определяют по формулам:
определяют по формулам:
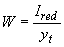 , (4.5)
, (4.5)
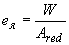 , (4.6)
, (4.6)
где 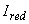 - момент инерции приведенного сечения относительно его центра тяжести, определяемый по формуле
- момент инерции приведенного сечения относительно его центра тяжести, определяемый по формуле
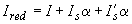 ; (4.7)
; (4.7)
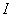 ,
, 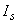 ,
, 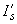 - моменты инерции сечения соответственно бетона, растянутой и сжатой арматуры;
- моменты инерции сечения соответственно бетона, растянутой и сжатой арматуры;
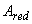 - площадь приведенного сечения, равная
- площадь приведенного сечения, равная
Дата добавления: 2017-02-20; просмотров: 4340;
