Расчет на продавливание элемента с поперечной арматурой 4 страница
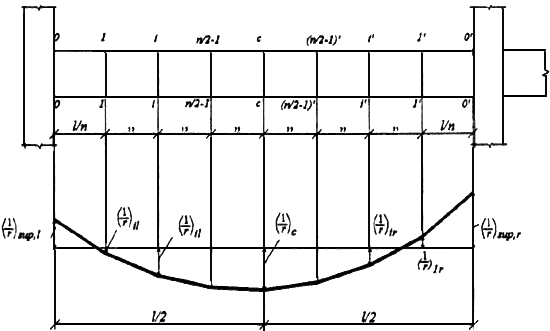
Черт.4.5. Эпюра кривизны в железобетонном элементе при общем случае определения прогиба
4.19. Для изгибаемых элементов постоянного сечения, имеющих трещины на каждом участке, в пределах которого изгибающий момент не меняет знак, допускается вычислять кривизну для наиболее напряженного сечения и принимать для остальных сечений такого участка кривизны изменяющимися пропорционально значениям изгибающего момента (черт.4.6).

Черт.4.6. Эпюры изгибающих моментов и кривизны в железобетонном элементе постоянного сечения
а - схема расположения нагрузки; б - эпюра моментов; в - эпюра кривизны
В этом случае для свободно опертых и консольных элементов максимальный прогиб определяют по формуле
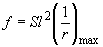 , (4.33)
, (4.33)
где 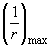 - полная кривизна в сечении с наибольшим изгибающим моментом, от нагрузки, при которой определяется прогиб;
- полная кривизна в сечении с наибольшим изгибающим моментом, от нагрузки, при которой определяется прогиб;
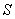 - коэффициент, принимаемый по табл.4.3.
- коэффициент, принимаемый по табл.4.3.
Таблица 4.3
| #G0Схема загружения свободно опертой балки | Коэффициент 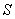
| Схема загружения консоли | Коэффициент 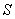
|
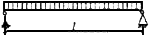
| 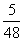
| 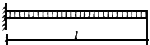
| 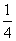
|
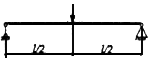
| 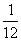
| 
| 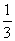
|
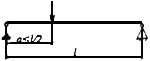
| 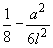
| 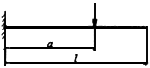
| 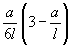
|
Примечание. При загружении элемента сразу по нескольким схемам 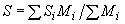 , где , где 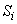 и и 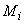 соответственно коэффициент соответственно коэффициент 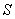 и момент и момент 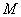 в середине пролета балки или в заделке консоли для каждой схемы загружения. В этом случае кривизна в середине пролета балки или в заделке консоли для каждой схемы загружения. В этом случае кривизна 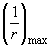 определяется при значении определяется при значении 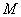 равном равном 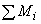 . .
|
Если прогиб, определяемый по формуле (4.33), превышает допустимый, то для слабо армированных элементов ( 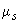 <0,5%) его значение рекомендуется уточнить за счет учета повышенной жесткости на участках без трещин и учета переменной жесткости на участках с трещинами; для свободно опертых балок, загруженных равномерно распределенной нагрузкой, это соответствует формуле
<0,5%) его значение рекомендуется уточнить за счет учета повышенной жесткости на участках без трещин и учета переменной жесткости на участках с трещинами; для свободно опертых балок, загруженных равномерно распределенной нагрузкой, это соответствует формуле
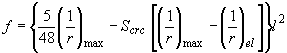 , (4.34)
, (4.34)
где 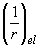 - полная кривизна в середине пролета, определенная без учета наличия трещин по формуле (4.37);
- полная кривизна в середине пролета, определенная без учета наличия трещин по формуле (4.37);
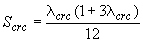
здесь 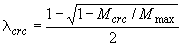
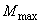 - максимальный момент от всех нагрузок;
- максимальный момент от всех нагрузок;
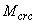 - момент образования трещин, определяемый согласно пп.4.4-4.8.
- момент образования трещин, определяемый согласно пп.4.4-4.8.
Для изгибаемых элементов с защемленными опорами прогиб в середине пролета может определяться по формуле
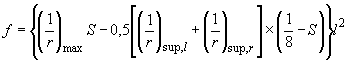 , (4.35)
, (4.35)
где 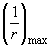 ,
, 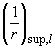 ,
, 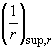 - кривизна соответственно в середине пролета, на левой и правой опорах;
- кривизна соответственно в середине пролета, на левой и правой опорах;
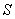 - коэффициент, определяемый по табл.4.3 как для свободно опертой балки.
- коэффициент, определяемый по табл.4.3 как для свободно опертой балки.
Во всех случаях прогиб принимается не менее прогиба, определенного по кривизнам без учета трещин.
4.20. Для изгибаемых элементов при 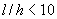 необходимо учитывать влияние поперечных сил на их прогиб. В этом случае полный прогиб равен сумме прогибов, обусловленных деформацией изгиба (см. пп.4.18 и 4.19) и деформацией сдвига
необходимо учитывать влияние поперечных сил на их прогиб. В этом случае полный прогиб равен сумме прогибов, обусловленных деформацией изгиба (см. пп.4.18 и 4.19) и деформацией сдвига 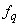 .
.
Прогиб 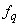 , обусловленный деформацией сдвига, определяют по формуле
, обусловленный деформацией сдвига, определяют по формуле
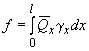 , (4.36)
, (4.36)
где 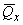 - поперечная сила в сечении
- поперечная сила в сечении 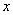 от действия единичной силы, приложенной в сечении, для которого определяется прогиб, в направлении этого прогиба;
от действия единичной силы, приложенной в сечении, для которого определяется прогиб, в направлении этого прогиба;
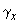 - угол сдвига элемента в сечении от действия внешней нагрузки, при которой определяется прогиб.
- угол сдвига элемента в сечении от действия внешней нагрузки, при которой определяется прогиб.
Значение 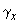 определяется по указаниям п.4.28.
определяется по указаниям п.4.28.
ОПРЕДЕЛЕНИЕ КРИВИЗНЫ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ
ОБЩИЕ ПОЛОЖЕНИЯ
4.21. Кривизну железобетонных элементов для вычисления их прогибов определяют:
а) для элементов или участков элемента, где в растянутой зоне не образуются нормальные к продольной оси трещины, согласно п.4.23;
б) для элементов или участков элемента, где в растянутой зоне имеются трещины, согласно пп.4.24-4.26.
Элементы или участки элементов рассматривают без трещин, если трещины не образуются (т.е. выполняется условие 4.2) при действии всех нагрузок (т.е. включая и кратковременные) с коэффициентом надежности по нагрузке 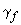 =1.
=1.
Кривизну железобетонных элементов с трещинами и без трещин можно определить на основе деформационной модели согласно п.4.27.
4.22. Полную кривизну изгибаемых, внецентренно сжатых и внецентренно растянутых элементов определяют по формуле:
- для участков без трещин в растянутой зоне
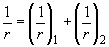 , (4.37)
, (4.37)
где 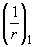 и
и 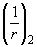 - кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и длительных нагрузок;
- кривизны соответственно от непродолжительного действия кратковременных нагрузок и от продолжительного действия постоянных и длительных нагрузок;
- для участков с трещинами в растянутой зоне
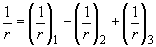 , (4.38)
, (4.38)
где 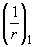 - кривизна от непродолжительного действия всex нагрузок, на которые производят расчет по деформациям;
- кривизна от непродолжительного действия всex нагрузок, на которые производят расчет по деформациям;
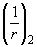 - кривизна от непродолжительного действия постоянных и длительных нагрузок;
- кривизна от непродолжительного действия постоянных и длительных нагрузок;
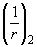 - кривизна от продолжительного действия постоянных и длительных нагрузок
- кривизна от продолжительного действия постоянных и длительных нагрузок
Примечание. При использовании формулы (4.37) кратковременную нагрузку, включающую в себя согласно СНиП 2.01.07-85* пониженное значение, следует принимать уменьшенной на это значение, учитываемое в этой формуле как длительная нагрузка.
Дата добавления: 2017-02-20; просмотров: 551;
