Расчет на продавливание элемента с поперечной арматурой 3 страница
где 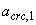 - ширина раскрытия трещин, определяемая согласно п.4.10 при
- ширина раскрытия трещин, определяемая согласно п.4.10 при  =1,4 и при действии постоянных и длительных нагрузок;
=1,4 и при действии постоянных и длительных нагрузок;
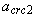 - то же, при
- то же, при  =1,0 и действии всех нагрузок (т.е. включая кратковременные);
=1,0 и действии всех нагрузок (т.е. включая кратковременные);
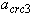 - то же, при
- то же, при  =1,0 и действии постоянных и длительных нагрузок.
=1,0 и действии постоянных и длительных нагрузок.
Ширину непродолжительного раскрытия трещин можно также определять по формуле
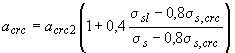 , (4.28а)
, (4.28а)
где значения 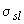 и
и 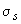 определяются согласно п.4.11 при действии соответственно суммы постоянных и длительных нагрузок и всех нагрузок;
определяются согласно п.4.11 при действии соответственно суммы постоянных и длительных нагрузок и всех нагрузок;
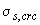 - см. п.4.13.
- см. п.4.13.
При отсутствии требований к конструкции по ограничению проницаемости и при выполнении условия
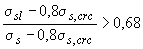 , (4.29)
, (4.29)
можно проверять только продолжительное раскрытие трещин, а при невыполнении условия (4.29) - только непродолжительное раскрытие.
Для изгибаемых элементов в формулах (4.28а) и (4.29) значения 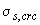 ,
, 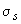 и
и 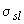 можно заменить соответственно на
можно заменить соответственно на 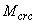 ,
, 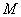 и
и 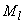 - момент от действия постоянных и длительных нагрузок.
- момент от действия постоянных и длительных нагрузок.
ПРИМЕРЫ РАСЧЕТА
Пример 42. Дано: железобетонная плита перекрытия с размерами поперечного сечения (для половины сечения плиты) по черт.4.4; бетон класса В25 ( 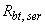 =1,55 МПа,
=1,55 МПа, 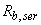 =18,5 МПа,
=18,5 МПа, 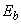 =30000 МПа); площадь сечения растянутой арматуры класса А400
=30000 МПа); площадь сечения растянутой арматуры класса А400  =760 мм
=760 мм  (2
(2 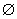 22); полный момент в середине пролета
22); полный момент в середине пролета 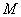 =69 кН·м; все нагрузки постоянные и длительные.
=69 кН·м; все нагрузки постоянные и длительные.
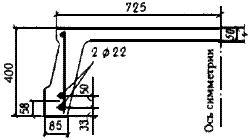
Черт.4.4. К примеру расчета 42
Требуется произвести расчет по раскрытию нормальных трещин.
Расчет. Из черт.4.4 имеем: 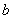 =85 мм,
=85 мм, 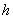 =400 мм,
=400 мм, 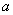 =58 мм,
=58 мм, 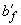 =725 мм;
=725 мм; 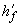 =50 мм.
=50 мм.
Определим момент образования трещин 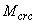 согласно п.4.5. Для этого определяем геометрические характеристики приведенного сечения при
согласно п.4.5. Для этого определяем геометрические характеристики приведенного сечения при 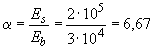 и
и 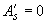 :
:

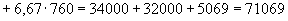 мм
мм  ;
;
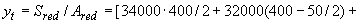
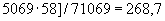 мм;
мм;
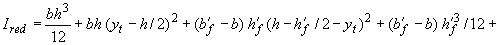
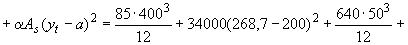
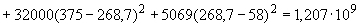 мм
мм 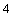 ;
;
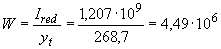 мм
мм 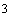 .
.
Учтем неупругие деформации растянутого бетона путем умножения 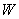 на коэффициент
на коэффициент  , равный согласно табл.4.1 1,30, т.е.
, равный согласно табл.4.1 1,30, т.е. 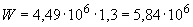 мм
мм 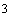 . Тогда
. Тогда
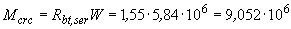 Н·мм
Н·мм 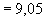 кН·м
кН·м 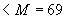 кН·м, т.е. трещины образуются и расчет по раскрытию трещин необходим.
кН·м, т.е. трещины образуются и расчет по раскрытию трещин необходим.
Определим напряжение в арматуре 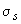 по формуле (4.13). Рабочая высота сечения
по формуле (4.13). Рабочая высота сечения 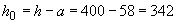 мм; коэффициент приведения
мм; коэффициент приведения 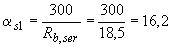 . Тогда при
. Тогда при 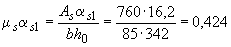 и
и 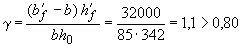 из графика на черт.4.2 находим коэффициент
из графика на черт.4.2 находим коэффициент 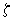 =0,9 и плечо внутренней пары сил равно
=0,9 и плечо внутренней пары сил равно 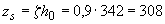 мм.
мм.
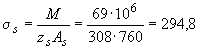 МПа.
МПа.
Определим расстояние между трещинами 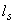 по формуле (4.22).
по формуле (4.22).
Поскольку высота растянутого бетона, равная 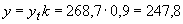 мм
мм 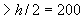 мм, площадь сечения растянутого бетона принимаем равной
мм, площадь сечения растянутого бетона принимаем равной
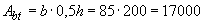 мм
мм  .
.
Тогда
 мм,
мм,
что меньше 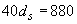 мм и меньше 400 мм, поэтому оставляем
мм и меньше 400 мм, поэтому оставляем 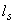 =246 мм.
=246 мм.
Значение 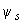 определим по формуле (4.26)
определим по формуле (4.26)
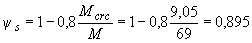 .
.
Определяем по формуле (4.10) ширину продолжительного раскрытия трещин, принимая  =1,4,
=1,4,  =0,5 и
=0,5 и 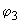 =1,0,
=1,0,
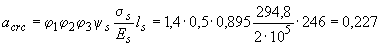 мм,
мм,
что меньше предельно допустимой ширины продолжительного раскрытия трещин, равной согласно п.4.2 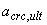 =0,3 мм.
=0,3 мм.
Пример 43. Дано: железобетонная плита фундамента с размерами поперечного сечения 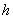 =300 мм,
=300 мм, 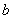 =1150 мм;
=1150 мм; 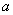 =42 мм; бетон класса В15 (
=42 мм; бетон класса В15 ( 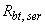 =1,1 МПа,
=1,1 МПа, 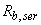 =11 МПа); рабочая арматура класса А400 с площадью сечения
=11 МПа); рабочая арматура класса А400 с площадью сечения  =923 мм
=923 мм  (6
(6 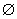 14); момент в расчетном сечении от постоянных и длительных нагрузок
14); момент в расчетном сечении от постоянных и длительных нагрузок 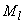 =50 кН·м, от кратковременных нагрузок
=50 кН·м, от кратковременных нагрузок 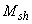 =10 кН·м; фундамент эксплуатируется в неагрессивных условиях (выше верхнего уровня грунтовых вод).
=10 кН·м; фундамент эксплуатируется в неагрессивных условиях (выше верхнего уровня грунтовых вод).
Требуется произвести расчет по раскрытию нормальных трещин.
Расчет. Определим момент образования трещин 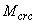 согласно пп.4.5-4.8. Поскольку
согласно пп.4.5-4.8. Поскольку  , упругий момент сопротивления
, упругий момент сопротивления 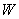 определим без учета арматуры, т.е.
определим без учета арматуры, т.е.
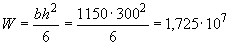 мм
мм 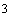 .
.
Учтем неупругие деформации растянутого бетона путем умножения 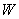 на коэффициент
на коэффициент  , равный согласно табл.4.1 1,30, т.е.
, равный согласно табл.4.1 1,30, т.е. 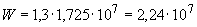 мм
мм 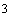 . Тогда
. Тогда 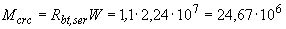 Н·мм
Н·мм 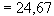 кН·м
кН·м 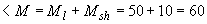 кН·м, т.е. трещины при действии полной нагрузки образуются и расчет по раскрытию трещин необходим.
кН·м, т.е. трещины при действии полной нагрузки образуются и расчет по раскрытию трещин необходим.
Проверим условие (4.29) с заменой напряжений 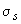 соответствующими моментами
соответствующими моментами
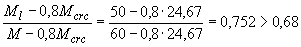 ,
,
следовательно, проверяем только продолжительное раскрытие трещин. Определяем напряжение в арматуре 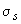 по формуле (4.13), принимая
по формуле (4.13), принимая  . Рабочая высота сечения
. Рабочая высота сечения 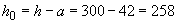 мм; коэффициент приведения
мм; коэффициент приведения  . Тогда при
. Тогда при 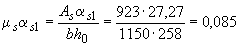 и
и 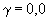 из графика на черт.4.3 находим
из графика на черт.4.3 находим 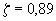 . Плечо внутренней пары сил равно
. Плечо внутренней пары сил равно  мм.
мм.
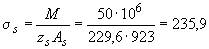 МПа.
МПа.
Для прямоугольного сечения высота растянутой зоны бетона с учетом неупругих деформаций равна 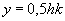 =0,5·300·0,9=135 мм
=0,5·300·0,9=135 мм 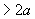 =2·42=84 мм и, кроме того,
=2·42=84 мм и, кроме того, 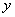 =135 мм
=135 мм 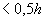 =150 мм, поэтому оставляем
=150 мм, поэтому оставляем 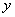 =135 мм и тогда
=135 мм и тогда 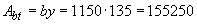 мм
мм  .
.
Расстояние между трещинами определим по формуле (4.22) 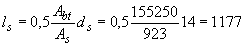 мм, что больше
мм, что больше 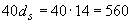 мм и более 400 мм, поэтому принимаем
мм и более 400 мм, поэтому принимаем 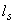 =400 мм.
=400 мм.
Значение 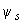 определяем по формуле (4.26), принимая
определяем по формуле (4.26), принимая  =50 кН·м.
=50 кН·м.
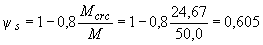 .
.
Определяем по формуле (4.10) ширину продолжительного раскрытия трещин, принимая  =1,4,
=1,4,  =0,5 и
=0,5 и 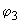 =1,0:
=1,0:
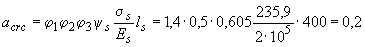 мм,
мм,
что меньше предельно допустимой ширины продолжительного раскрытия трещин, равной 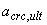 =0,3 мм.
=0,3 мм.
Пример 44. Дано: железобетонная колонна промышленного здания, с размерами поперечного сечения 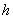 =500 мм,
=500 мм, 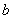 =400 мм;
=400 мм; 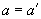 =50 мм; бетон класса В15 (
=50 мм; бетон класса В15 ( 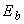 =24000 МПа,
=24000 МПа, 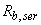 =11 МПа,
=11 МПа, 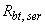 =1,1 МПа); рабочая арматура класса А400 с площадью сечения
=1,1 МПа); рабочая арматура класса А400 с площадью сечения 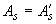 =1232 мм
=1232 мм  (2
(2 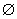 28); усилия от постоянных и длительных нагрузок:
28); усилия от постоянных и длительных нагрузок: 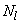 =500 кН,
=500 кН, 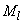 =150 кН·м; усилия от кратковременной (ветровой) нагрузки:
=150 кН·м; усилия от кратковременной (ветровой) нагрузки: 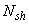 =0,0;
=0,0; 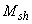 =90 кН·м.
=90 кН·м.
Требуется рассчитать колонну по раскрытию трещин
Расчет. Определяем момент образования трещин 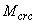 согласно пп.4.5-4.8.
согласно пп.4.5-4.8.
Поскольку 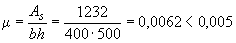 , определяем значения
, определяем значения 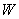 и
и 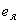 с учетом арматуры при коэффициенте приведения
с учетом арматуры при коэффициенте приведения 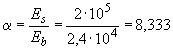 . Для прямоугольного сечения с симметричной арматурой
. Для прямоугольного сечения с симметричной арматурой 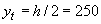 мм, а момент инерции
мм, а момент инерции 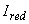 равен
равен
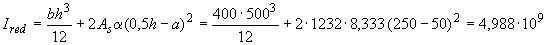 мм
мм 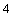 .
.
Тогда 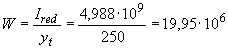 мм
мм 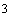 .
.
Площадь приведенного сечения равна
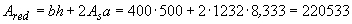 мм
мм 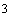 .*
.*
________________
* Текст соответствует оригиналу. - Примечание "КОДЕКС".
Тогда 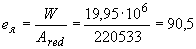 мм.
мм.
Учитываем неупругие деформации растянутого бетона путем умножения 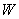 на коэффициент
на коэффициент  =1,3 (см. табл.4.1), т.е.
=1,3 (см. табл.4.1), т.е. 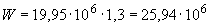 мм.
мм.
Определяем момент 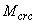 по формуле (4.4), принимая
по формуле (4.4), принимая 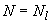 =500 кН,
=500 кН,
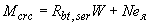 =1,1·25,94·10
=1,1·25,94·10 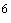 +500000·90,5=73,76·10
+500000·90,5=73,76·10 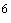 Н·мм=73,76 кН·м
Н·мм=73,76 кН·м 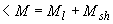 =150+90=240 кН·м, т.е. трещины при действии всех нагрузок образуются и расчет по раскрытию трещин необходим.
=150+90=240 кН·м, т.е. трещины при действии всех нагрузок образуются и расчет по раскрытию трещин необходим.
Определяем напряжение в растянутой арматуре при действии всех нагрузок по формуле (4.19).
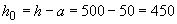 мм
мм 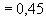 м.
м.
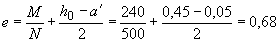 м.
м.
При 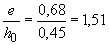 и
и 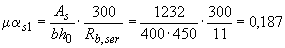 из табл.4.2 находим
из табл.4.2 находим 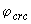 =0,54. Тогда
=0,54. Тогда 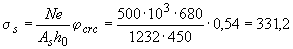 МПа.
МПа.
Аналогично определяем напряжение 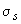 при действии постоянных и длительных нагрузок, т.е. принимая
при действии постоянных и длительных нагрузок, т.е. принимая  =150 кН·м и
=150 кН·м и 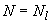 =500 кН.
=500 кН.
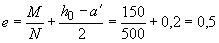 м.
м.
При 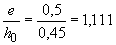 и
и 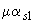 =0,187 из табл.4.2 находим
=0,187 из табл.4.2 находим 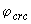 =0,32.
=0,32.
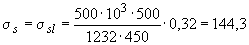 МПа.
МПа.
Определим также напряжение 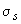 при действии момента
при действии момента 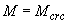 =73,76 кН·м и силы
=73,76 кН·м и силы 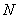 =500 кН.
=500 кН.
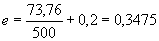 м; по
м; по 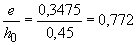 и
и 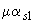 =0,187 находим
=0,187 находим 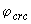 =0,08;
=0,08; 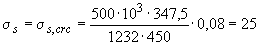 МПа.
МПа.
Проверим условие (4.29)
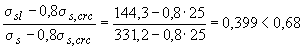 ,
,
т.е. условие (4.29) не выполняется, следовательно, проверяем только непродолжительное раскрытие трещин, определяя 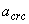 по формуле (4.28а). Для этого предварительно определяем
по формуле (4.28а). Для этого предварительно определяем 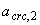 по формуле (4.10) при
по формуле (4.10) при  =1,0 и
=1,0 и 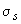 =331,2 МПа. По формуле (4.25) имеем
=331,2 МПа. По формуле (4.25) имеем 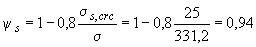 .
.
Определяем расстояние между трещинами 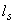 согласно п.4.12. Для этого вычислим высоту растянутой зоны бетона по формуле (4.23), принимая
согласно п.4.12. Для этого вычислим высоту растянутой зоны бетона по формуле (4.23), принимая 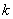 =0,90, а
=0,90, а 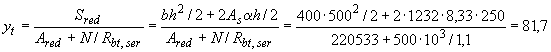 мм,
мм,
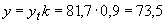 мм
мм 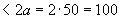 мм.
мм.
Принимаем 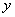 =100 мм и тогда площадь сечения растянутого бетона равна
=100 мм и тогда площадь сечения растянутого бетона равна  мм
мм 
а 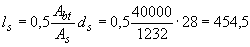 мм
мм 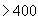 мм.
мм.
Принимаем 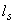 =400 м.
=400 м.
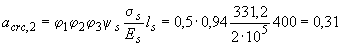 мм;
мм;
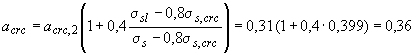 мм,
мм,
что меньше предельно допустимой ширины непродолжительного раскрытия трещин, равной 0,4 мм.
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ ПО ДЕФОРМАЦИЯМ
ОБЩИЕ ПОЛОЖЕНИЯ
4.15. Расчет элементов железобетонных конструкций по деформациям производят с учетом эксплуатационных требований, предъявляемых к конструкции.
Расчет по деформациям следует производить на действие:
постоянных, временных длительных и кратковременных нагрузок при ограничении деформаций технологическими или конструктивными требованиями;
постоянных и временных длительных нагрузок при ограничении деформаций эстетико-психологическими требованиями.
4.16. Значения предельно допустимых деформаций элементов принимают согласно СНиП 2.01.07-85* и нормативным документам на отдельные виды конструкций.
РАСЧЕТ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ ПО ПРОГИБАМ
4.17. Расчет железобетонных элементов по прогибам производят из условия
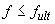 , (4.30)
, (4.30)
где 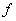 - прогиб железобетонного элемента от действия внешней нагрузки;
- прогиб железобетонного элемента от действия внешней нагрузки;
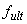 - значение предельно допустимого прогиба железобетонного элемента.
- значение предельно допустимого прогиба железобетонного элемента.
Прогибы железобетонных конструкций определяют по общим правилам строительной механики в зависимости от изгибных, сдвиговых и осевых деформационных характеристик железобетонных элементов в сечениях по его длине (кривизны, углов сдвига, относительных продольных деформаций).
В тех случаях, когда прогибы железобетонных элементов, в основном, зависят от изгибных деформаций, значение прогибов определяют по кривизне элемента согласно пп.4.18 и 4.19.
4.18. Прогиб железобетонных элементов, обусловленный деформацией изгиба, определяют по формуле
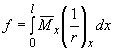 , (4.31)
, (4.31)
где 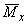 - изгибающий момент в сечении
- изгибающий момент в сечении 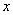 от действия единичной силы, приложенной в сечении, для которого определяется прогиб, в направлении этого прогиба;
от действия единичной силы, приложенной в сечении, для которого определяется прогиб, в направлении этого прогиба;
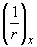 - полная кривизна элемента в сечении от внешней нагрузки, при которой определяется прогиб.
- полная кривизна элемента в сечении от внешней нагрузки, при которой определяется прогиб.
В общем случае формулу (4.31) можно реализовать путем разбиения элемента на ряд участков, определяя кривизну на границах этих участков (с учетом наличия или отсутствия трещин и знака кривизны) и перемножения эпюр моментов 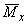 и кривизны
и кривизны 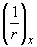 по длине элемента, принимая линейное распределение кривизны в пределах каждого участка. В этом случае при определении прогиба в середине пролета формула (4.31) приобретает вид
по длине элемента, принимая линейное распределение кривизны в пределах каждого участка. В этом случае при определении прогиба в середине пролета формула (4.31) приобретает вид
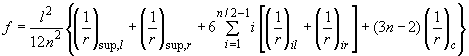 , (4.32)
, (4.32)
где 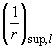 ,
, 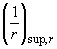 - кривизна элемента соответственно на левой и правой опорах;
- кривизна элемента соответственно на левой и правой опорах;
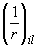 ,
, 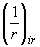 - кривизна элемента в симметрично расположенных сечениях
- кривизна элемента в симметрично расположенных сечениях 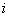 и
и 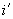 (при
(при 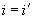 ) соответственно слева и справа от оси симметрии (середины пролета, черт.4.5);
) соответственно слева и справа от оси симметрии (середины пролета, черт.4.5);
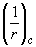 - кривизна элемента в середине пролета;
- кривизна элемента в середине пролета;
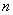 - четное число равных участков, на которое разделяют пролет, принимаемое не менее 6;
- четное число равных участков, на которое разделяют пролет, принимаемое не менее 6;
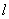 - пролет элемента.
- пролет элемента.
В формулах (4.31) и (4.32) кривизны 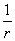 определяют по указаниям пп.4.21-4.27. При этом знак кривизны принимают в соответствии с эпюрой кривизны.
определяют по указаниям пп.4.21-4.27. При этом знак кривизны принимают в соответствии с эпюрой кривизны.
Дата добавления: 2017-02-20; просмотров: 474;
