Расчет железобетонных элементов по наклонным сечениям на действие поперечных сил 5 страница
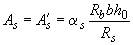 , (3.96)
, (3.96)
где 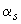 определяется по графику черт.3.28 в зависимости от значений
определяется по графику черт.3.28 в зависимости от значений
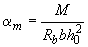
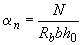 .
.
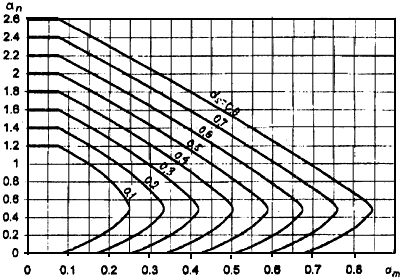
Черт.3.28. Графики несущей способности внецентренно сжатых элементов прямоугольного сечения с симметричной арматурой
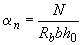 ;
; 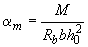 ;
; 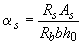
3.58. Расчет сжатых элементов из бетона классов В15-В35 на действие продольной силы, приложенной с эксцентриситетом, принятым согласно п.3.49, равным случайному эксцентриситету 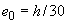 , при
, при 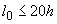 допускается производить из условия
допускается производить из условия
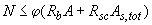 , (3.97)
, (3.97)
где 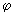 - коэффициент, определяемый по формуле
- коэффициент, определяемый по формуле
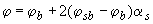 , (3.98)
, (3.98)
но принимаемый не более 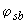 .
.
Здесь 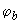 и
и 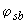 - коэффициенты, принимаемые по табл.3.5 и 3.6.
- коэффициенты, принимаемые по табл.3.5 и 3.6.
Таблица 3.5
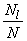
| #G0Коэффициент 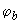 при при 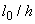
| |||||||
| 0,93 | 0,92 | 0,91 | 0,90 | 0,89 | 0,88 | 0,86 | 0,84 | |
| 0,5 | 0,92 | 0,91 | 0,90 | 0,89 | 0,86 | 0,82 | 0,77 | 0,71 |
| 1,0 | 0,92 | 0,91 | 0,89 | 0,87 | 0,83 | 0,76 | 0,68 | 0,60 |
Таблица 3.6
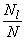
| #G0Коэффициент 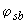 при при 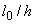
| |||||||
А. При 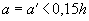 и при отсутствии промежуточных стержней (см. эскиз) или площади сечения этих стержней менее и при отсутствии промежуточных стержней (см. эскиз) или площади сечения этих стержней менее 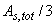
| ||||||||
| 0,93 | 0,92 | 0,91 | 0,90 | 0,89 | 0,88 | 0,86 | 0,83 | |
| 0,5 | 0,92 | 0,91 | 0,91 | 0,90 | 0,88 | 0,87 | 0,83 | 0,79 |
| 1,0 | 0,92 | 0,91 | 0,90 | 0,90 | 0,88 | 0,85 | 0,80 | 0,74 |
Б. При 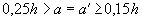 или при площади промежуточных стержней (см. эскиз), равной или более или при площади промежуточных стержней (см. эскиз), равной или более 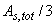 независимо от независимо от 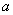
| ||||||||
| 0,92 | 0,92 | 0,91 | 0,89 | 0,87 | 0,85 | 0,82 | 0,79 | |
| 0,5 | 0,92 | 0,91 | 0,90 | 0,88 | 0,85 | 0,81 | 0,76 | 0,71 |
| 1,0 | 0,92 | 0,91 | 0,89 | 0,87 | 0,83 | 0,77 | 0,70 | 0,62 |
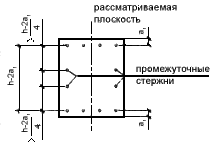
| Обозначения, принятые в табл.3.5 и 3.6:
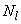 - продольная сила от действия постоянных и длительных нагрузок. - продольная сила от действия постоянных и длительных нагрузок.
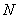 - продольная сила от всех нагрузок. - продольная сила от всех нагрузок.
|
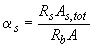 ; (3.99)
; (3.99)
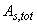 - площадь сечения всей арматуры в сечении;
- площадь сечения всей арматуры в сечении;
при 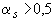 можно, не пользуясь формулой (3.98), принимать
можно, не пользуясь формулой (3.98), принимать 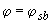 .
.
Прямоугольные сечения с несимметричной арматурой
3.59. Проверку прочности прямоугольных сечений с несимметричной арматурой производят из условия (3.91) п.3.56, определяя высоту сжатой зоны по формуле
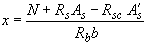 ; (3.100)
; (3.100)
при этом, если 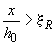 (см. табл.3.2), высоту сжатой зоны корректируют, вычисляя по формуле
(см. табл.3.2), высоту сжатой зоны корректируют, вычисляя по формуле
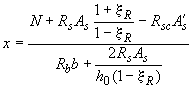 . (3.101)
. (3.101)
3.60. Площади сечения сжатой и растянутой арматуры, соответствующие минимуму их суммы, определяются по формулам:
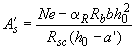 ; (3.102)
; (3.102)
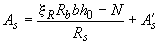 , (3.103)
, (3.103)
где 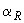 и
и 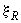 - определяются по табл.3.2 и принимаются не более соответственно 0,4 и 0,55;
- определяются по табл.3.2 и принимаются не более соответственно 0,4 и 0,55;
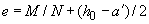 .
.
При отрицательном значении 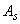 , вычисленном по формуле (3.103), площадь сечения арматуры
, вычисленном по формуле (3.103), площадь сечения арматуры 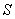 принимается минимальной по конструктивным требованиям, но не менее величины
принимается минимальной по конструктивным требованиям, но не менее величины
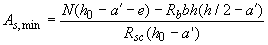 , (3.104)
, (3.104)
а площадь сечения арматуры 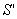 определяется:
определяется:
при отрицательном значении 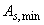 - по формуле
- по формуле
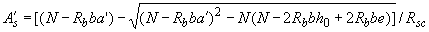 ; (3.105)
; (3.105)
при положительном значении 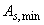 - по формуле
- по формуле
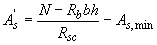 . (3.106)
. (3.106)
Если принятая площадь сечения сжатой арматуры 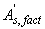 значительно превышает ее значение, вычисленное по формуле (3.102) (например, при отрицательном его значении), площадь сечения растянутой арматуры может быть уменьшена исходя из формулы
значительно превышает ее значение, вычисленное по формуле (3.102) (например, при отрицательном его значении), площадь сечения растянутой арматуры может быть уменьшена исходя из формулы
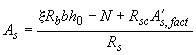 , (3.107)
, (3.107)
где 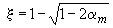 ,
,
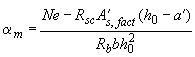 .
.
Если сжатая арматура отсутствует или не учитывается в расчете, площадь сечения растянутой арматуры определяется всегда только по формуле (3.107), при этом должно выполняться условие 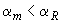 .
.
Двутавровые сечения с симметричной арматурой
3.60. Проверку прочности двутавровых сечений с симметричной арматурой, сосредоточенной в полках (черт.3.29), производят следующим образом.
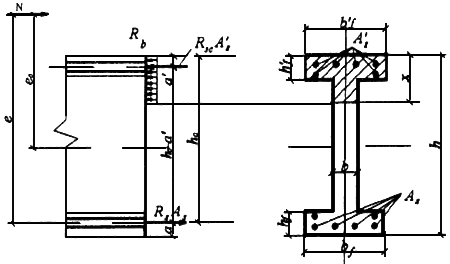
Черт.3.29. Схема усилий в поперечном двутавровом сечении внецентренно сжатого элемента
Если соблюдается условие
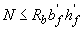 (3.108)
(3.108)
(т.е. граница сжатой зоны проходит в полке), расчет производится как для прямоугольного сечения шириной 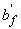 в соответствии с п.3.56.
в соответствии с п.3.56.
Если условие (3.108) не соблюдается (т.е. граница сжатой зоны проходит в ребре), прочность сечения проверяют из условия
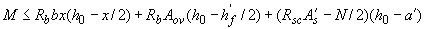 , (3.109)
, (3.109)
где высоту сжатой зоны 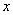 принимают равной:
принимают равной:
а) при 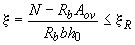
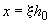 ;
;
б) при 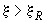
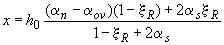 , (3.110)
, (3.110)
где 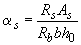 ;
; 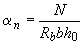 ;
; 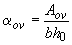 ;
;
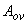 - площадь сжатых свесов полки, равная
- площадь сжатых свесов полки, равная 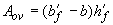 ;
;
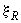 - см. табл.3.2.
- см. табл.3.2.
Примечание. При переменной высоте свесов полок значение 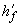 принимается равным средней высоте свесов.
принимается равным средней высоте свесов.
3.61. Требуемое количество симметричной арматуры двутавровых сечений определяется следующим образом.
При соблюдении условия (3.108) подбор арматуры производят как для прямоугольного сечения шириной 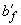 согласно п.3.57.
согласно п.3.57.
Если условие (3.108) не соблюдается, подбор арматуры производят в зависимости от относительной высоты сжатой зоны, равной
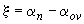 : (3.111)
: (3.111)
а) при 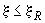
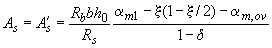 , (3.112)
, (3.112)
б) 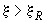
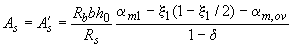 , (3.113)
, (3.113)
где относительную высоту сжатой зоны 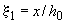 определяют из формулы (3.110), вычисляя
определяют из формулы (3.110), вычисляя 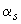 по формуле
по формуле
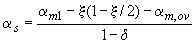 , (3.114)
, (3.114)
при этом 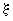 принимается не более 1,0.
принимается не более 1,0.
В формулах (3.111)-(3.114):
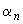 ,
, 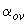 - см. п.3.60;
- см. п.3.60;
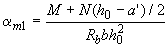 ;
; 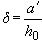 ;
; 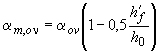 .
.
Кольцевые сечения
3.62. Проверка прочности кольцевых сечений (черт.3.30) при соотношении внутреннего и наружного радиусов 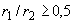 и арматуре, равномерно распределенной по окружности (при продольных стержнях не менее 7), производится следующим образом в зависимости от относительной площади сжатой зоны бетона
и арматуре, равномерно распределенной по окружности (при продольных стержнях не менее 7), производится следующим образом в зависимости от относительной площади сжатой зоны бетона
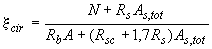 ; (3.115)
; (3.115)
а) при 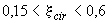 - из условия
- из условия
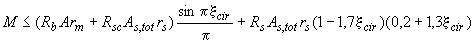 ; (3.116)
; (3.116)
б) при 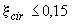 - из условия
- из условия
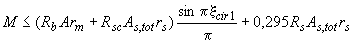 (3.117)
(3.117)
где
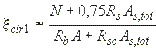 ; (3.118)
; (3.118)
в) при 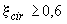 - из условия
- из условия
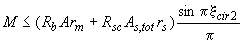 ; (3.119)
; (3.119)
где
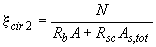 . (3.120)
. (3.120)
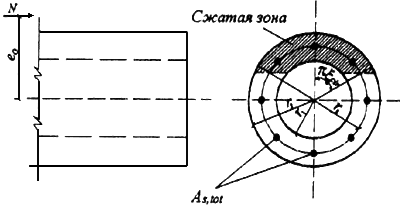
Черт.3.30. Схема, принимаемая при расчете кольцевого сечения сжатого элемента
В формулах (3.115)-(3.120):
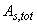 - площадь сечения всей продольной арматуры;
- площадь сечения всей продольной арматуры;
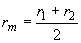 ;
;
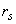 - радиус окружности, проходящей через центры тяжести стержней продольной арматуры.
- радиус окружности, проходящей через центры тяжести стержней продольной арматуры.
Момент 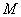 определяется с учетом прогиба элементов согласно пп.3.53-3.55.
определяется с учетом прогиба элементов согласно пп.3.53-3.55.
3.63. Проверку прочности, а также определение необходимого количества продольной арматуры для кольцевых сечений, указанных в п.3.62, при 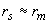 и классе арматуры не выше А400 допускается производить с помощью графиков черт.3.31, используя формулы:
и классе арматуры не выше А400 допускается производить с помощью графиков черт.3.31, используя формулы:
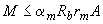 ; (3.121)
; (3.121)
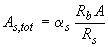 , (3.122)
, (3.122)
где значения 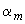 и
и 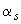 определяются по графику в зависимости от значений соответственно
определяются по графику в зависимости от значений соответственно 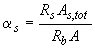 и
и 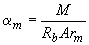 , а также
, а также 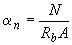 . При этом момент
. При этом момент 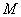 определяется с учетом прогиба элемента согласно пп.3.53-3.55.
определяется с учетом прогиба элемента согласно пп.3.53-3.55.
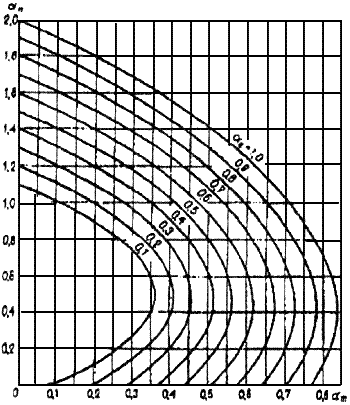
Черт.3.31. Графики несущей способности внецентренно сжатых элементов кольцевого сечения
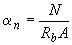 ;
; 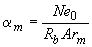 ;
; 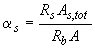
Круглые сечения
3.64. Прочность круглых сечений (черт.3.32) с арматурой, равномерно распределенной по окружности (при числе продольных стержней не менее 7), при классе арматуры не выше А400 проверяется из условия
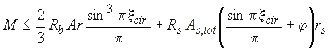 , (3.123)
, (3.123)
где 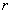 - радиус поперечного сечения;
- радиус поперечного сечения;
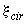 - относительная площадь сжатой зоны бетона, определяемая следующим образом:
- относительная площадь сжатой зоны бетона, определяемая следующим образом:
при выполнении условия
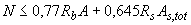 (3.124)
(3.124)
из решения уравнения
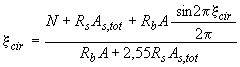 ; (3.125)
; (3.125)
при невыполнении условия (3.124) - из решения уравнения
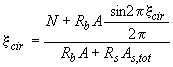 ; (3.126)
; (3.126)
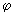 - коэффициент, учитывающий работу растянутой арматуры и принимаемый равным: при выполнении условия (3.124)
- коэффициент, учитывающий работу растянутой арматуры и принимаемый равным: при выполнении условия (3.124) 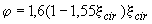 , но не более 1,0; при невыполнении условий (3.124)
, но не более 1,0; при невыполнении условий (3.124) 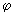 =0;
=0;
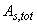 - площадь сечения всей продольной арматуры;
- площадь сечения всей продольной арматуры;
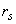 - радиус окружности, проходящей через центры тяжести стержней продольной арматуры.
- радиус окружности, проходящей через центры тяжести стержней продольной арматуры.

Черт.3.32. Схема, принимаемая при расчете круглого сечения внецентренно сжатого элемента
Момент 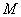 определяется с учетом прогиба элементов согласно пп.3.53-3.55.
определяется с учетом прогиба элементов согласно пп.3.53-3.55.
3.65. Проверку прочности, а также определение необходимого количества продольной арматуры для круглых сечений, указанных в п.3.64, допускается производить с помощью графиков черт.3.33, используя формулы:
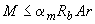 ; (3.127)
; (3.127)
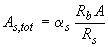 , (3.128)
, (3.128)
где значения 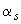 и
и 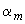 определяются по графику в зависимости от значений соответственно
определяются по графику в зависимости от значений соответственно 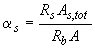 и
и 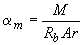 , а также от
, а также от 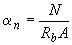 . При этом момент
. При этом момент 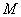 определяется с учетом прогиба элемента согласно пп.3.53-3.55.
определяется с учетом прогиба элемента согласно пп.3.53-3.55.
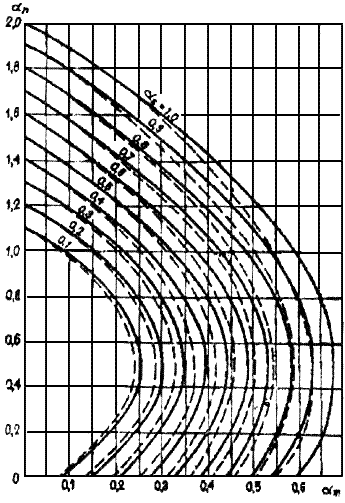
Условные обозначения:
 при
при 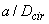 =0,05
=0,05
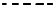 при
при 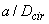 =0,10
=0,10
Черт.3.33. Графики несущей способности внецентренно сжатых элементов круглого сечения
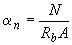 ;
; 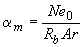 ;
; 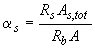
Расчет элементов на косое внецентренное сжатие
3.66. Для элементов прямоугольного сечения с симметричной арматурой в виде 4-х угловых стержней расчет на косое внецентренное сжатие можно производить из условия
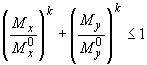 , (3.129)
, (3.129)
где  и
и 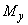 - моменты от внешней нагрузки относительно центра тяжести сечения в плоскостях симметрии
- моменты от внешней нагрузки относительно центра тяжести сечения в плоскостях симметрии 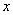 и
и 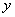 ;
;
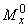 и
и 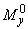 - предельные моменты в плоскостях симметрии
- предельные моменты в плоскостях симметрии 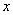 и
и 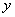 относительно центра сечения, равные правой части условия (3.91) п.3.56.
относительно центра сечения, равные правой части условия (3.91) п.3.56.
Значения 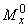 и
и 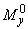 можно также определять с помощью графика на черт.3.28 по формуле
можно также определять с помощью графика на черт.3.28 по формуле
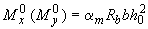 , (3.130)
, (3.130)
где 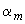 определяется по графику на черт.3.28 в зависимости от
определяется по графику на черт.3.28 в зависимости от 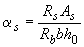 и
и 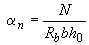 ;
;
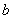 и
и 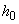 - ширина и рабочая высота сечения применительно к направлению рассматриваемого момента;
- ширина и рабочая высота сечения применительно к направлению рассматриваемого момента;
при этом для соответствующего направления должно выполняться условие 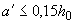 .
.
Показатель степени 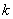 в условии (3.129) определяется по формулам:
в условии (3.129) определяется по формулам:
если 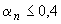 ,
, 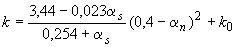 ; (3.131)
; (3.131)
если 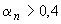 ,
, 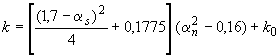 , (3.132)
, (3.132)
но не более 1,6,
где 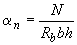 ;
; 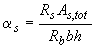 ;
; 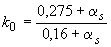 .
.
Примеры расчета
Прямоугольные сечения с симметричной арматурой
Пример 22. Дано: колонна среднего этажа рамного каркаса с сечением размерами 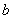 =400 мм,
=400 мм, 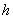 =500 мм;
=500 мм; 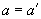 =40 мм; бетон класса В25 (
=40 мм; бетон класса В25 ( 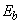 =300000 МПа,
=300000 МПа, 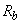 =14,5 МПа); арматура класса А400 (
=14,5 МПа); арматура класса А400 ( 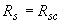 =355 МПа); площадь ее сечения
=355 МПа); площадь ее сечения 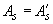 =1232 мм
=1232 мм  (2
(2  28); продольная сила и изгибающие моменты в опорном сечении: от вертикальных нагрузок: всех
28); продольная сила и изгибающие моменты в опорном сечении: от вертикальных нагрузок: всех 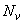 =650 кН,
=650 кН, 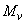 =140 кН·м, постоянных и длительных
=140 кН·м, постоянных и длительных 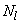 =620 кН,
=620 кН, 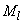 =130 кН·м; от ветровых нагрузок
=130 кН·м; от ветровых нагрузок 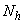 =50 кН,
=50 кН, 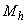 =73 кН·м; высота этажа
=73 кН·м; высота этажа 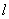 =6 м.
=6 м.
Требуется проверить прочность опорного сечения колонны.
Расчет. 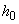 =500-40=460 мм. Расчет ведем с учетом влияния прогиба согласно п.3.53. Поскольку рассматриваемое сечение опорное и колонна у этой опоры имеет податливую заделку, принимаем
=500-40=460 мм. Расчет ведем с учетом влияния прогиба согласно п.3.53. Поскольку рассматриваемое сечение опорное и колонна у этой опоры имеет податливую заделку, принимаем 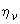 =1,0. Для вычисления коэффициента
=1,0. Для вычисления коэффициента 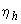 принимаем согласно п.3.55, б расчетную длину колонны равной
принимаем согласно п.3.55, б расчетную длину колонны равной 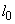 =1,2·6=7,2 м. При этом
=1,2·6=7,2 м. При этом 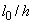 =7,2/0,5=14,4>4, т.е. учет прогиба обязателен.
=7,2/0,5=14,4>4, т.е. учет прогиба обязателен.
Усилия от всех нагрузок равны 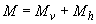 =140+73=213 кН·м,
=140+73=213 кН·м, 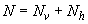 =650+50=700 кН. При этом
=650+50=700 кН. При этом
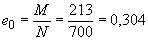 м
м 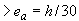 , т.е. согласно п.3.49 значение момента
, т.е. согласно п.3.49 значение момента 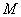 не корректируем.
не корректируем.
Дата добавления: 2017-02-20; просмотров: 959;
