Расчет железобетонных элементов по наклонным сечениям на действие поперечных сил 8 страница
По значениям 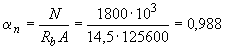 ,
, 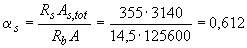 и
и
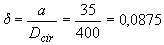 на графике находим
на графике находим 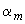 =0,375.
=0,375.
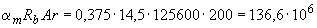 Н·мм
Н·мм 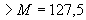 кН·м,
кН·м,
т.е. прочность сечения обеспечена.
Элементы, работающие на косое внецентренное сжатие
Пример 33.* Дано: прямоугольное сечение колонны с размерами 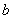 =400 мм,
=400 мм, 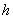 =500 мм; бетон класса В25 (
=500 мм; бетон класса В25 ( 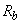 =14,5 МПа); продольная арматура класса А400 (
=14,5 МПа); продольная арматура класса А400 ( 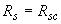 =355 МПа) расположена в сечении согласно черт.3.35; в сечении одновременно действует сила
=355 МПа) расположена в сечении согласно черт.3.35; в сечении одновременно действует сила 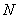 =2600 кН и изгибающие моменты: в плоскости, параллельной размеру
=2600 кН и изгибающие моменты: в плоскости, параллельной размеру 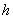 ,
,  =150 кН·м; в плоскости, параллельной размеру
=150 кН·м; в плоскости, параллельной размеру 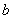 ,
, 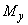 =100 кН·м; моменты
=100 кН·м; моменты  и
и 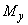 даны с учетом прогиба колонны.
даны с учетом прогиба колонны.
________________
* Нумерация соответствует оригиналу. - Примечание "КОДЕКС".
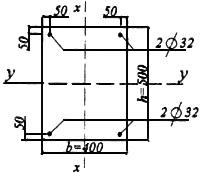
Черт.3.35. К примеру расчета 33
Требуется проверить прочность сечения.
Расчет. Поскольку арматура задана в виде 4-х угловых стержней, прочность сечения проверяем согласно п.3.66. Оси симметрии, параллельные размерам 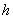 и
и 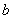 , обозначим
, обозначим 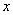 и
и 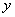 . Определим предельные моменты
. Определим предельные моменты 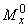 и
и 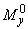 .
.
При действии момента в плоскости оси 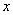 принимаем
принимаем 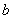 =400 мм,
=400 мм, 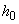 =500-50=450 мм.
=500-50=450 мм. 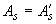 =1609 мм
=1609 мм  (2
(2 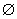 32). Поскольку
32). Поскольку 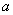 =50 мм <0,15
=50 мм <0,15 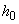 =0,15·450=67,5 мм, расчет можем производить с помощью графика на черт.3.28. Для этого определяем
=0,15·450=67,5 мм, расчет можем производить с помощью графика на черт.3.28. Для этого определяем 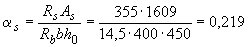 и
и 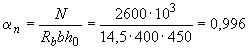 .
.
На графике этим значениям соответствует 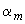 =0,24. Следовательно,
=0,24. Следовательно, 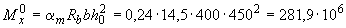 Н·мм
Н·мм 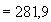 кН·м.
кН·м.
При действии момента в плоскости оси 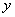 принимаем
принимаем 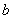 =500 мм,
=500 мм, 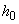 =400-50=350 мм. Поскольку
=400-50=350 мм. Поскольку 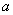 =50 мм <0,15
=50 мм <0,15 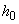 =0,15·350=52,5 мм, момент
=0,15·350=52,5 мм, момент 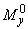 также можно определить с помощью графика на черт.3.28.
также можно определить с помощью графика на черт.3.28.
Значениям 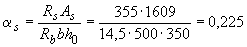 и
и 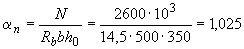 на графике соответствует
на графике соответствует 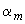 =0,23. Следовательно,
=0,23. Следовательно, 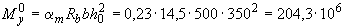 Н·мм
Н·мм 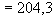 кН·м.
кН·м.
Определим показатель степени 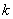 . Поскольку
. Поскольку 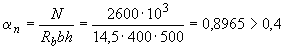 , используем формулу (3.132), вычислив значения
, используем формулу (3.132), вычислив значения
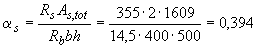 и
и 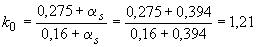 .
.
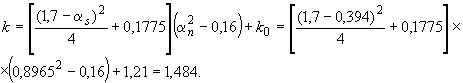
Проверяем условие (3.129):
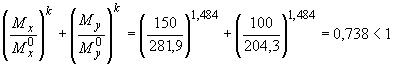 ,
,
т.е. прочность сечения обеспечена.
Расчет наклонных сечений
Пример 34. Дано: колонна многоэтажного рамного каркаса с сечением размерами 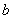 =400 мм,
=400 мм, 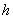 =600 мм;
=600 мм; 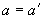 =50 мм; бетон класса В25 (
=50 мм; бетон класса В25 ( 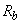 =14,5 МПа,
=14,5 МПа, 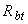 =1,05 МПа); хомуты, расположенные по граням колонны, из арматуры класса А240 (
=1,05 МПа); хомуты, расположенные по граням колонны, из арматуры класса А240 ( 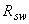 =170 МПа) диаметром 12 мм (
=170 МПа) диаметром 12 мм ( 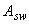 =226 мм
=226 мм  ) шагом
) шагом 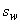 =400 мм; изгибающие моменты в верхнем и нижнем опорных сечениях равны
=400 мм; изгибающие моменты в верхнем и нижнем опорных сечениях равны 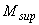 =350 кН·м,
=350 кН·м, 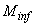 =250 кН·м и растягивают соответственно левую и правую грани колонны; продольная сила
=250 кН·м и растягивают соответственно левую и правую грани колонны; продольная сила 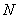 =572 кН; длина колонны (расстояние между опорными сечениями)
=572 кН; длина колонны (расстояние между опорными сечениями) 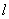 =3,3 м.
=3,3 м.
Требуется проверить прочность колонны на действие поперечной силы.
Расчет. 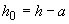 =600-50=550 мм. Расчет производим согласно пп.3.30-3.32 с учетом рекомендаций п.3.52.
=600-50=550 мм. Расчет производим согласно пп.3.30-3.32 с учетом рекомендаций п.3.52.
Поперечная сила в колонне равна
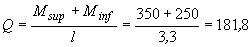 кH.
кH.
Поскольку поперечная сила постоянна по длине колонны, длину проекции наклонного сечения принимаем максимально возможной, т.е. равной 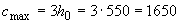 мм
мм 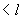 =2800 мм.
=2800 мм.
По формуле (3.84) определяем коэффициент 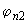 , принимая
, принимая 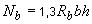 =1,3·14,5·400·600=4524·10
=1,3·14,5·400·600=4524·10 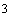 Н=4524 кН
Н=4524 кН 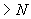 = 572 кН,
= 572 кН,
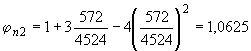 .
.
Поскольку 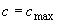 ,
, 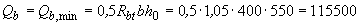 H, а после умножения на
H, а после умножения на
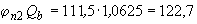 кН.
кН.
Значение 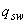 определяем по формуле (3.48)
определяем по формуле (3.48)
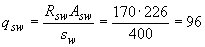 Н/мм.
Н/мм.
Определяем усилие в хомутах 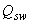 , принимая
, принимая 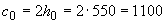 мм,
мм,
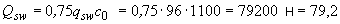 кН.
кН.
Проверяем условие (3.49), умножая его правую часть на 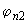 :
: 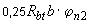 =0,25·1,05·400·1,0625=111,6 Н/м
=0,25·1,05·400·1,0625=111,6 Н/м 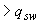 =96 Н/мм.
=96 Н/мм.
Поскольку условие (3.49) не выполняется, принимаем 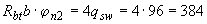 Н/мм, а следовательно,
Н/мм, а следовательно, 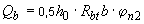 =0,5·550·384=105600 Н =105,6 кН
=0,5·550·384=105600 Н =105,6 кН
Проверяем условие (3.44):
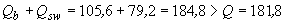 кН,
кН,
т.е. прочность наклонного сечения по поперечной силе обеспечена.
ЦЕНТРАЛЬНО И ВНЕЦЕНТРЕННО РАСТЯНУТЫЕ ЭЛЕМЕНТЫ
ЦЕНТРАЛЬНО РАСТЯНУТЫЕ ЭЛЕМЕНТЫ
3.67. Расчет по прочности сечений центрально растянутых элементов следует производить из условия
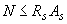 , (3.133)
, (3.133)
где  - площадь сечения всей продольной арматуры.
- площадь сечения всей продольной арматуры.
ВНЕЦЕНТРЕННО РАСТЯНУТЫЕ ЭЛЕМЕНТЫ
3.68. Расчет нормальных сечений внецентренно растянутых элементов в общем случае производят на основе нелинейной деформационной модели согласно пп.3.72-3.76.
Расчет прямоугольных сечений внецентренно растянутых элементов с арматурой, расположенной у перпендикулярных плоскости изгиба граней элемента, при направлении эксцентриситета в плоскости симметрии сечения допускается производить по предельным усилиям согласно пп.3.69 и 3.70.
3.69. Проверку прочности прямоугольных сечений внецентренно растянутых элементов следует производить в зависимости от положения продольной силы 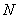 :
:
а) если продольная сила 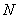 приложена между равнодействующими усилий в арматуре
приложена между равнодействующими усилий в арматуре 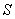 и
и 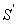 (черт.3.36, а), т.е. при
(черт.3.36, а), т.е. при 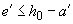 , - из условий
, - из условий
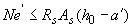 ; (3.134)
; (3.134)
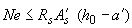 ; (3.135)
; (3.135)
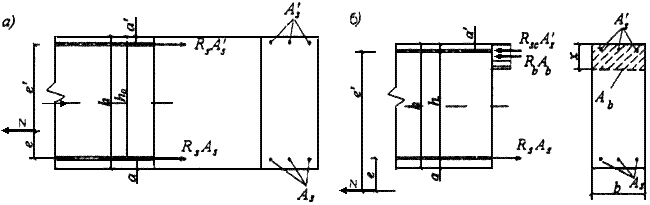
Черт.3.36. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси внецентренно растянутого железобетонного элемента, при расчете его по прочности
б) если продольная сила 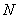 приложена за пределами расстояния между равнодействующими усилий в арматуре
приложена за пределами расстояния между равнодействующими усилий в арматуре 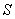 и
и 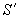 (черт.3.36, б), т.е. при
(черт.3.36, б), т.е. при 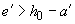 - из условия
- из условия
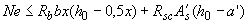 (3.136)
(3.136)
при этом высота сжатой зоны 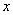 определяется по формуле
определяется по формуле
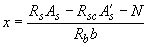 . (3.137)
. (3.137)
Если полученное из расчета по формуле (3.137) значение 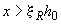 , в условие (3.136) подставляют
, в условие (3.136) подставляют 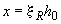 , где
, где 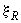 определяют по табл.3.2.
определяют по табл.3.2.
При 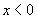 прочность сечения проверяют из условия (3.134).
прочность сечения проверяют из условия (3.134).
При симметричном армировании прочность независимо от значения 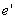 проверяют из условия (3.134).
проверяют из условия (3.134).
Примечание. Если при 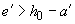 высота сжатой зоны, определенная без учета сжатой арматуры,
высота сжатой зоны, определенная без учета сжатой арматуры, 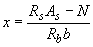 меньше
меньше 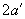 , расчетную несущую способность можно несколько увеличить, произведя расчет по формулам (3.136) и (3.137) без учета сжатой арматуры.
, расчетную несущую способность можно несколько увеличить, произведя расчет по формулам (3.136) и (3.137) без учета сжатой арматуры.
3.70. Требуемое количество продольной арматуры определяется следующим образом:
а) при 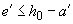 определяется площадь сечения арматуры
определяется площадь сечения арматуры 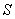 и
и 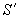 соответственно по формулам:
соответственно по формулам:
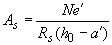 ; (3.138)
; (3.138)
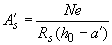 ; (3.139)
; (3.139)
б) при 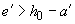 определяется площадь сечения растянутой арматуры
определяется площадь сечения растянутой арматуры  по формуле:
по формуле:
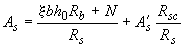 ; (3.140)
; (3.140)
где 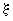 определяется по формуле
определяется по формуле
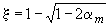 , (3.141)
, (3.141)
здесь
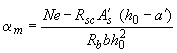 . (3.142)
. (3.142)
При этом должно выполняться условие 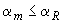 (см. табл.3.2). В противном случае следует увеличить сечение сжатой арматуры
(см. табл.3.2). В противном случае следует увеличить сечение сжатой арматуры 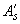 , повысить класс бетона или увеличить размеры сечения.
, повысить класс бетона или увеличить размеры сечения.
Если 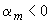 , площадь сечения растянутой арматуры
, площадь сечения растянутой арматуры  определяется по формуле (3.138).
определяется по формуле (3.138).
Площадь симметричной арматуры независимо от значения 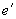 подбирается по формуле (3.138).
подбирается по формуле (3.138).
Примечание. При 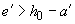 необходимое количество арматуры, определенное по формуле (3.138), можно снизить, если значение
необходимое количество арматуры, определенное по формуле (3.138), можно снизить, если значение 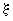 , определенное по формуле (3.141) при
, определенное по формуле (3.141) при 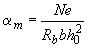 , окажется меньше
, окажется меньше 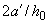 . В этом случае площадь сечения растянутой арматуры
. В этом случае площадь сечения растянутой арматуры  определяется по формуле (3.140), используя упомянутое значение
определяется по формуле (3.140), используя упомянутое значение 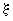 при
при 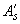 =0.
=0.
3.71. Расчет наклонных сечений растянутых элементов при действии поперечных сил производится аналогично расчету изгибаемых элементов в соответствии с пп.3.30-3.35. При этом значение поперечной силы, воспринимаемой бетоном в наклонном сечении, 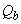 , а также правая часть условия (3.49) делится на коэффициент
, а также правая часть условия (3.49) делится на коэффициент
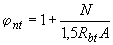 . (3.143)
. (3.143)
На этот же коэффициент 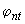 делится связанное с
делится связанное с 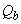 значение
значение 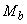 .
.
Примеры расчета
Пример 35. Дано: растянутая ветвь двухветвевой колонны с поперечным сечением размерами 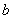 =500 мм,
=500 мм, 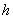 =200 мм;
=200 мм; 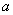 =
= 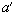 = 40 мм; продольная арматура класса А400 (
= 40 мм; продольная арматура класса А400 ( 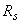 =
= 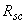 =355 МПа); площадь ее сечения
=355 МПа); площадь ее сечения 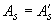 =982 мм
=982 мм  (2
(2 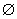 25); бетон класса В25 (
25); бетон класса В25 ( 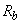 =14,5 МПа); продольная растягивающая сила
=14,5 МПа); продольная растягивающая сила 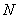 =44 кН; максимальный изгибающий момент
=44 кН; максимальный изгибающий момент 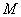 =43 кН·м.
=43 кН·м.
Требуется проверить прочность нормального сечения
Расчет. 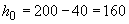 мм.
мм.
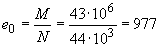 мм;
мм;
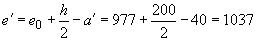 мм;
мм;
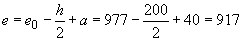 мм.
мм.
Поскольку арматура симметричная, прочность проверим из условия (3.134):
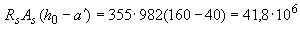 Н·мм
Н·мм 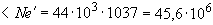 Н·мм, т.е. условие (3.134) не выполняется.
Н·мм, т.е. условие (3.134) не выполняется.
Так как 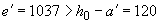 мм, а высота сжатой зоны
мм, а высота сжатой зоны 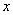 , определенная без учета сжатой арматуры, т.е. равная
, определенная без учета сжатой арматуры, т.е. равная 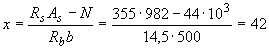 мм, меньше
мм, меньше 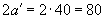 мм, согласно примечанию к п.3.69 проверим прочность из условия (3.136), принимая
мм, согласно примечанию к п.3.69 проверим прочность из условия (3.136), принимая 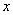 =42 мм и
=42 мм и 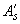 =0:
=0:
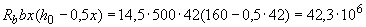 Н·мм
Н·мм 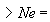
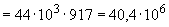 Н·мм,
Н·мм,
т.е. прочность обеспечена.
Пример 36. Дано: прямоугольное сечение размерами 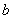 =1000 мм,
=1000 мм, 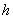 =200 мм;
=200 мм; 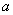 =
= 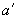 =35 мм; бетон класса В15 (
=35 мм; бетон класса В15 ( 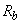 =8,5 МПа); продольная арматура класса А400 (
=8,5 МПа); продольная арматура класса А400 ( 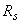 =
= 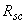 =355 МПа); площадь сечения арматуры
=355 МПа); площадь сечения арматуры 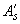 =1005 мм
=1005 мм  (5
(5 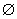 16); растягивающая сила
16); растягивающая сила 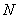 =160 кН; изгибающий момент
=160 кН; изгибающий момент 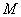 =116 кН·м.
=116 кН·м.
Требуется определить площадь сечения арматуры 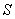 .
.
Расчет. 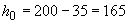 мм;
мм;
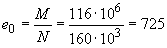 мм;
мм;
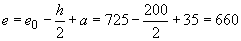 мм;
мм;
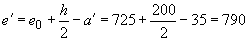 мм.
мм.
Так как 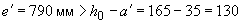 мм, определим необходимую площадь сечения растянутой арматуры согласно п.3.70, б.
мм, определим необходимую площадь сечения растянутой арматуры согласно п.3.70, б.
Вычислим значение
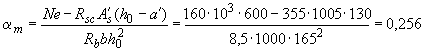 .
.
Так как 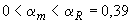 (см. табл.3.2), значение
(см. табл.3.2), значение  определяется по формуле (3.140). Для этого вычисляем
определяется по формуле (3.140). Для этого вычисляем 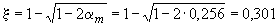 .
.
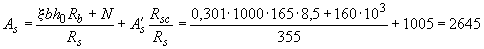 мм
мм  .
.
Принимаем  =3079 мм
=3079 мм  (5
(5 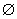 28).
28).
Пример 37. Дано: растянутая ветвь двухветвевой колонны с сечением размерами 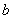 =500 мм,
=500 мм, 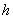 =200 мм;
=200 мм; 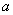 =
= 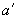 =40 мм; бетон класса В25 (
=40 мм; бетон класса В25 ( 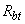 =1,05 МПа); хомуты, расположенные по граням, из арматуры класса А400 (
=1,05 МПа); хомуты, расположенные по граням, из арматуры класса А400 ( 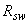 =285 МПа); продольная растягивающая сила
=285 МПа); продольная растягивающая сила 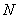 =44 кН; поперечная сила
=44 кН; поперечная сила 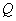 =130 кН; расстояние в свету между перемычками двухветвевой колонны
=130 кН; расстояние в свету между перемычками двухветвевой колонны 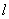 =600 мм.
=600 мм.
Требуется определить диаметр и шаг хомутов.
Расчет. 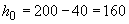 мм. Расчет производим согласно п.3.33, а с учетом указаний п.3.71.
мм. Расчет производим согласно п.3.33, а с учетом указаний п.3.71.
По формуле (3.143) определяем коэффициент 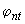 , принимая
, принимая 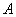 =
= 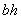 =500·200=100000 мм
=500·200=100000 мм  :
:
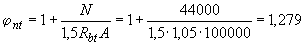 .
.
Поскольку в пределах между перемычками поперечная сила постоянна, длину проекции наклонного сечения принимаем максимально возможной, т.е.
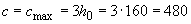 мм
мм 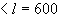 мм.
мм.
При 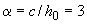 и
и 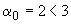 определяем
определяем
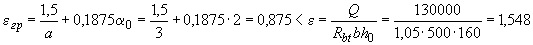 .
.
Следовательно, требуемую интенсивность хомутов определяем по формуле (3.48), при этом величину 1,5, характеризующую значение 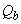 , делим на
, делим на 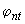 =1,279:
=1,279:
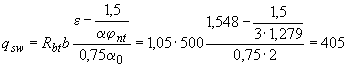 Н/мм.
Н/мм.
Максимально допустимый шаг, согласно п.3.35, равен
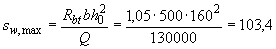 мм.
мм.
Принимаем шаг хомутов 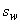 =100 мм <
=100 мм <  , и тогда
, и тогда
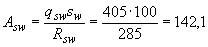 мм
мм  .
.
Принимаем два хомута диаметром по 10 мм ( 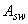 =157 мм
=157 мм  ).
).
Дата добавления: 2017-02-20; просмотров: 1165;
