Расчет железобетонных элементов по наклонным сечениям на действие поперечных сил 9 страница
РАСЧЕТ НОРМАЛЬНЫХ СЕЧЕНИЙ НА ОСНОВЕ НЕЛИНЕЙНОЙ ДЕФОРМАЦИОННОЙ МОДЕЛИ
3.72. При расчете по прочности усилия и деформации в нормальном сечении определяют на основе нелинейной деформационной модели, использующей уравнения равновесия внешних сил и внутренних усилий в сечении элементов, а также следующие положения:
- распределение относительных деформаций бетона и арматуры по высоте сечения элемента принимают по линейному закону (гипотеза плоских сечений, см. черт.3.39);
- связь между осевыми сжимающими напряжениями бетона 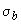 и относительными его деформациями
и относительными его деформациями 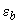 принимают в виде двухлинейной диаграммы (черт.3.37), согласно которой напряжения
принимают в виде двухлинейной диаграммы (черт.3.37), согласно которой напряжения 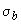 определяются следующим образом:
определяются следующим образом:
при 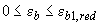
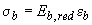 ;
;
при 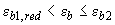
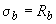 ;
;
где 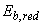 - приведенный модуль деформации бетона, равный
- приведенный модуль деформации бетона, равный
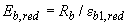 ;
;
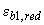 =0,0015;
=0,0015;
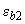 =0,0035;
=0,0035;
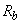 - см. табл.2.2;
- см. табл.2.2;
- сопротивление бетона растянутой зоны не учитывается (т.е. принимается 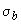 =0) за исключением расчета бетонных элементов, указанных в п.1.4, б, а также бетонных элементов, в которых не допускаются трещины; в этих элементах связь между осевыми растягивающими напряжениями бетона
=0) за исключением расчета бетонных элементов, указанных в п.1.4, б, а также бетонных элементов, в которых не допускаются трещины; в этих элементах связь между осевыми растягивающими напряжениями бетона 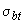 и относительными его деформациями также принимаются в виде двухлинейной диаграммы с заменой
и относительными его деформациями также принимаются в виде двухлинейной диаграммы с заменой 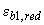 на
на 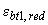 =0,0008;
=0,0008; 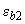 на
на 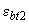 =0,00015;
=0,00015; 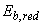 на
на 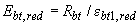 , где
, где 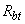 - см. табл.2.2;
- см. табл.2.2;
- связь между напряжениями арматуры 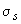 и относительными ее деформациями
и относительными ее деформациями 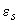 принимают в виде двухлинейной диаграммы (черт.3.38), согласно которой напряжения
принимают в виде двухлинейной диаграммы (черт.3.38), согласно которой напряжения 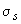 принимают равными:
принимают равными:
при 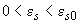
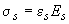 ;
;
при 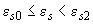
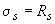 ,
,
где 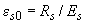 ;
;
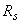 - см. табл.2.6;
- см. табл.2.6;
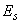 =2·10
=2·10 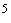 МПа;
МПа;
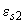 =0,025.
=0,025.
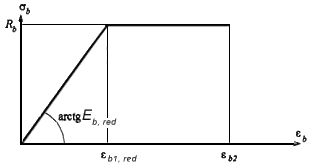
Черт.3.37. Двухлинейная диаграмма состояния сжатого бетона
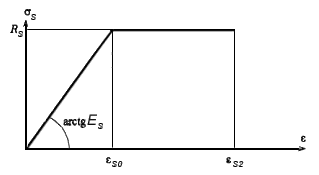
Черт.3.38. Диаграмма состояния растянутой арматуры
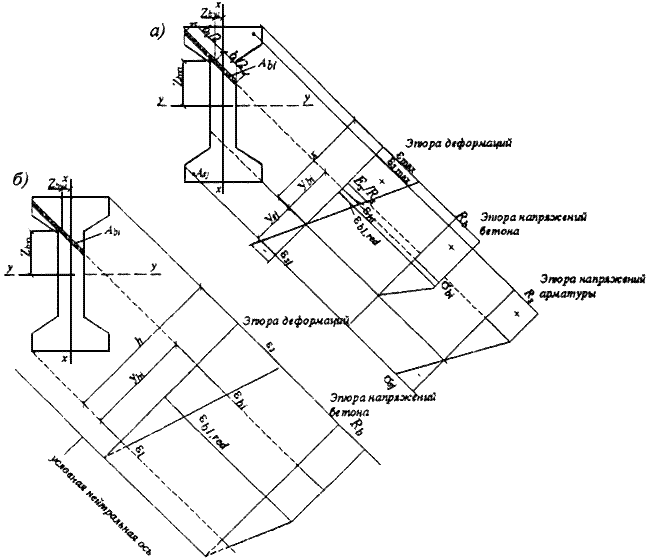
Черт.3.39. Эпюры деформаций и напряжений в сечении, нормальном к продольной оси железобетонного элемента, в общем случае расчета по прочности
а) - двухзначная эпюра деформаций
б) - однозначная эпюра деформаций
3.73. Переход от эпюры напряжений в бетоне к обобщенным внутренним усилиям рекомендуется осуществлять с помощью процедуры численного интегрирования по нормальному сечению. Для этого нормальное сечение в направлении плоскости изгиба (нормальной нейтральной оси) разделяется на участки малой ширины, напряжения в которых принимают равномерно распределенными и соответствующими деформациям на уровне середины ширины участка.
В общем случае положение нейтральной оси и максимальные деформации (черт.3.39) определяют из уравнений равновесия внешних и внутренних усилий:
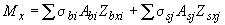 ; (3.144)
; (3.144)
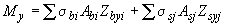 ; (3.145)
; (3.145)
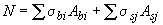 ; (3.146)
; (3.146)
где  и
и 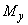 - моменты внешних сил относительно выбранных координатных осей, действующих в плоскости осей соответственно
- моменты внешних сил относительно выбранных координатных осей, действующих в плоскости осей соответственно 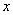 и
и 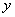 ;
;
 ,
, 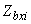 ,
,  ,
, 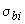 - площадь, координаты центра тяжести
- площадь, координаты центра тяжести 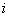 -го участка бетона и напряжение на уровне его центра тяжести.
-го участка бетона и напряжение на уровне его центра тяжести.
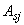 ,
, 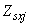 ,
, 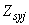 ,
, 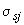 - площадь, координаты центра тяжести
- площадь, координаты центра тяжести 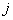 -го стержня арматуры и напряжение в нем.
-го стержня арматуры и напряжение в нем.
Напряжения 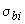 и
и 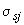 определяются в соответствии с диаграммами на черт.3.37 и 3.38.
определяются в соответствии с диаграммами на черт.3.37 и 3.38.
Растягивающие напряжения арматуры 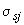 и бетона
и бетона 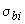 , а также продольную растягивающую силу
, а также продольную растягивающую силу 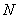 рекомендуется учитывать в уравнениях (3.144)-(3.146) со знаком "минус".
рекомендуется учитывать в уравнениях (3.144)-(3.146) со знаком "минус".
Координатные оси 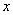 и
и 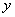 рекомендуется проводить через центр тяжести бетонного сечения.
рекомендуется проводить через центр тяжести бетонного сечения.
3.74. Расчет нормальных сечений железобетонных элементов по прочности производят из условий
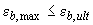 ; (3.147)
; (3.147)
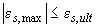 , (3.148)
, (3.148)
где 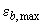 и
и 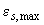 - относительные деформации соответственно наиболее сжатого волокна бетона и наиболее растянутого стержня арматуры от действия внешних нагрузок, определяемые из решения уравнений (3.144)-(3.146);
- относительные деформации соответственно наиболее сжатого волокна бетона и наиболее растянутого стержня арматуры от действия внешних нагрузок, определяемые из решения уравнений (3.144)-(3.146);
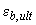 и
и 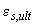 - предельные значения относительных деформаций соответственно сжатого бетона и растянутой арматуры, принимаемые согласно п.3.75.
- предельные значения относительных деформаций соответственно сжатого бетона и растянутой арматуры, принимаемые согласно п.3.75.
Для изгибаемых и внецентренно сжатых бетонных элементов, в которых не допускаются трещины, расчет производится с учетом работы растянутого бетона в поперечном сечении элемента из условия
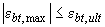 , (3.149)
, (3.149)
где 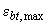 - относительная деформация наиболее растянутого волокна бетона, определяемая из решения уравнений (3.144)-(3.146);
- относительная деформация наиболее растянутого волокна бетона, определяемая из решения уравнений (3.144)-(3.146);
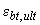 - предельное значение относительной деформации растянутого бетона, принимаемое согласно п.3.75.
- предельное значение относительной деформации растянутого бетона, принимаемое согласно п.3.75.
3.75. Предельное значение относительных деформаций бетона 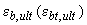 принимают при двухзначной эпюре деформаций (сжатие и растяжение) в поперечном сечении элемента равными
принимают при двухзначной эпюре деформаций (сжатие и растяжение) в поперечном сечении элемента равными 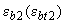 (см. п.3.72).
(см. п.3.72).
При внецентренном сжатии или растяжении элементов и распределении в поперечном сечении элемента деформаций бетона одного знака предельные значения относительных деформаций бетона 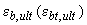 определяют в зависимости от отношения относительных деформаций бетона на противоположных сторонах сечения
определяют в зависимости от отношения относительных деформаций бетона на противоположных сторонах сечения 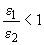 по формулам
по формулам
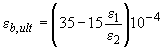 ; (3.150)
; (3.150)
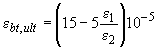 . (3.151)
. (3.151)
Предельное значение относительной деформации растянутой арматуры 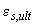 принимают равным 0,025.
принимают равным 0,025.
3.76. Расчет на основе нелинейной деформационной модели производится с помощью компьютерных программ.
При действии в нормальном сечении двух моментов  и
и 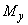 по обеим координатным осям
по обеим координатным осям 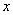 и
и 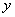 и продольной сжимающей силы компьютерную программу рекомендуется составлять на основе следующего алгоритма:
и продольной сжимающей силы компьютерную программу рекомендуется составлять на основе следующего алгоритма:
1. Задаются направлением нейтральной оси: в 1-м приближении это направление определяется как для упругого материала, т.е. принимается угол наклона нейтральной оси к оси 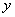 равным
равным 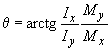 .
.
2. Определяют характер эпюры деформаций путем сравнения внешней продольной силы 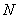 и внутреннего усилия
и внутреннего усилия 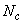 , определенного по формуле (3.146) при значениях
, определенного по формуле (3.146) при значениях 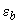 в крайних точках, равных
в крайних точках, равных 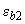 и 0. При
и 0. При 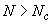 - эпюра однозначная, при
- эпюра однозначная, при 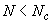 - эпюра двухзначная.
- эпюра двухзначная.
3. При двухзначной эпюре деформаций последовательными приближениями подбирают такую высоту сжатой зоны 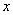 , при которой выполняется равенство (3.146); при этом в крайней сжатой точке принимается
, при которой выполняется равенство (3.146); при этом в крайней сжатой точке принимается 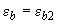 , деформации сжатого бетона каждого
, деформации сжатого бетона каждого 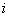 -го участка принимаются равными
-го участка принимаются равными  , а деформации каждого
, а деформации каждого 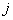 -го стержня арматуры -
-го стержня арматуры - 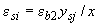 , где
, где 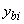 и
и 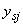 - расстояния от нейтральной оси до центра тяжести соответственно
- расстояния от нейтральной оси до центра тяжести соответственно 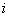 -го участка бетона и
-го участка бетона и 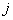 -го стержня арматуры. В случае, если
-го стержня арматуры. В случае, если 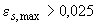 , принимается
, принимается 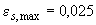 , и тогда
, и тогда 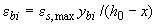 ,
, 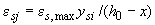 , где
, где 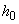 - расстояние между наиболее растянутым стержнем арматуры и наиболее сжатой точкой бетона в направлении, нормальном нейтральной оси. Деформации растянутой арматуры принимаются со знаком "минус".
- расстояние между наиболее растянутым стержнем арматуры и наиболее сжатой точкой бетона в направлении, нормальном нейтральной оси. Деформации растянутой арматуры принимаются со знаком "минус".
4. При однозначной эпюре деформаций последовательными приближениями подбирают такое отношение деформаций в крайних точках 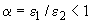 , при котором выполняется равенство (3.146); при этом в крайней сжатой точке всегда принимается деформация
, при котором выполняется равенство (3.146); при этом в крайней сжатой точке всегда принимается деформация 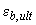 , определенная по формуле (3.150), деформации сжатого бетона каждого
, определенная по формуле (3.150), деформации сжатого бетона каждого 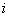 -го участка принимаются равными
-го участка принимаются равными 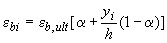 , а деформации каждого
, а деформации каждого 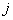 -го стержня -
-го стержня - 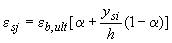 , где
, где 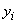 и
и 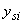 - расстояния от наименее сжатой точки до центра тяжести соответственно
- расстояния от наименее сжатой точки до центра тяжести соответственно 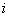 -го участка бетона и
-го участка бетона и 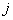 -го стержня арматуры в направлении, нормальном нейтральной оси,
-го стержня арматуры в направлении, нормальном нейтральной оси, 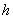 - см. черт.3.39, б.
- см. черт.3.39, б.
5. По формулам (3.144) и (3.145) определяются моменты внутренних усилий 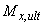 и
и 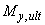 . Если оба эти момента оказываются больше или меньше соответствующих внешних моментов
. Если оба эти момента оказываются больше или меньше соответствующих внешних моментов  и
и 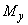 относительно тех же осей, то прочность сечения считается обеспеченной или необеспеченной.
относительно тех же осей, то прочность сечения считается обеспеченной или необеспеченной.
Если один из моментов (например 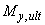 ) меньше соответствующего внешнего момента (т.е.
) меньше соответствующего внешнего момента (т.е. 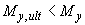 ), а другой больше (т.е.
), а другой больше (т.е. 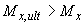 ), задаются другим углом наклона нейтральной оси
), задаются другим углом наклона нейтральной оси 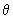 (большим, чем ранее принятый) и вновь проводят аналогичный расчет.
(большим, чем ранее принятый) и вновь проводят аналогичный расчет.
При действии растягивающей силы или при ее отсутствии расчет можно производить аналогичным образом. При расчете бетонных элементов с учетом работы растянутого бетона значения 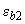 заменяются на
заменяются на 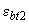 , а
, а 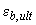 на
на 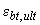 (см. пп.3.72 и 3.75).
(см. пп.3.72 и 3.75).
ЭЛЕМЕНТЫ, РАБОТАЮЩИЕ НА КРУЧЕНИЕ С ИЗГИБОМ
Дата добавления: 2017-02-20; просмотров: 404;
