Расчет железобетонных элементов по наклонным сечениям на действие поперечных сил 2 страница
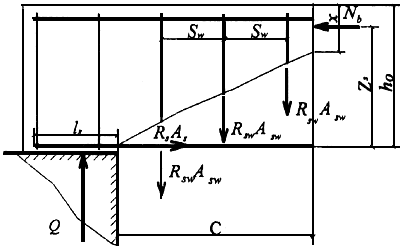
Черт.3.18. Схема усилий в наклонном сечении при расчете его по изгибающему моменту

Черт.3.19. Определение расчетного значения момента при расчете наклонного сечения
а - для свободно опертой балки; б - для консоли
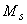 - момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения;
- момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения;
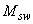 - момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения (точка 0).
- момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения (точка 0).
Момент 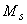 определяют по формуле
определяют по формуле
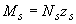 , (3.70)
, (3.70)
где 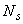 - усилие в продольной растянутой арматуре, принимаемое равным
- усилие в продольной растянутой арматуре, принимаемое равным 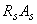 , а в зоне анкеровки определяемое согласно п.3.45;
, а в зоне анкеровки определяемое согласно п.3.45;
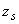 - плечо внутренней пары сил, определяемое по формуле
- плечо внутренней пары сил, определяемое по формуле
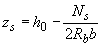 (где
(где 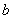 - ширина сжатой грани);
- ширина сжатой грани);
но при наличии сжатой арматуры принимаемое не менее 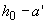 ; допускается также принимать
; допускается также принимать 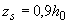 .
.
Момент 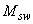 при поперечной арматуре в виде хомутов, нормальных к продольной оси элемента, определяют по формуле
при поперечной арматуре в виде хомутов, нормальных к продольной оси элемента, определяют по формуле
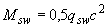 , (3.71)
, (3.71)
где 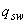 определяют по формуле (3.48) п.3.31, а
определяют по формуле (3.48) п.3.31, а  принимают не более
принимают не более  .
.
Если хомуты в пределах длины  меняют свою интенсивность с
меняют свою интенсивность с 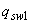 у начала наклонного сечения на
у начала наклонного сечения на 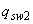 , момент
, момент 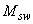 определяют по формуле:
определяют по формуле:
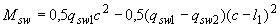 , (3.72)
, (3.72)
где 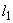 - длина участка с интенсивностью хомутов
- длина участка с интенсивностью хомутов 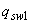 .
.
Значение  определяют согласно п.3.46.
определяют согласно п.3.46.
3.44. Расчет на действие момента производят для наклонных сечений, расположенных в местах обрыва продольной арматуры, а также у грани крайней свободной опоры балок и у свободного конца консолей при отсутствии у продольной арматуры специальных анкеров.
Кроме того, рассчитываются наклонные сечения в местах резкого изменения высоты элемента (например, в подрезках).
3.45. При пересечении наклонного сечения с продольной растянутой арматурой, не имеющей анкеров в пределах зоны анкеровки, усилие 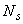 определяется по формуле:
определяется по формуле:
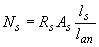 , (3.73)
, (3.73)
где 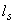 - расстояние от конца арматуры до точки пересечения с ней наклонного сечения;
- расстояние от конца арматуры до точки пересечения с ней наклонного сечения;
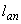 - длина зоны анкеровки, равная
- длина зоны анкеровки, равная 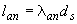 ,
,
где
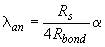 (3.74)
(3.74)
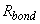 - расчетное сопротивление сцепления арматуры с бетоном, равное
- расчетное сопротивление сцепления арматуры с бетоном, равное
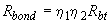 ,
,
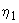 - коэффициент, учитывающий влияние вида поверхности арматуры и принимаемый равным:
- коэффициент, учитывающий влияние вида поверхности арматуры и принимаемый равным:
2,5 - для арматуры классов А300, А400, А500;
2,0 - для арматуры класса В500;
1,5 - для арматуры класса А240;
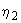 - коэффициент, учитывающий влияние диаметра арматуры и принимаемый равным:
- коэффициент, учитывающий влияние диаметра арматуры и принимаемый равным:
1,0 - при диаметре 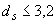 мм,
мм,
0,9 - при диаметрах 36 и 40 мм;
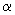 - коэффициент, учитывающий влияние поперечного обжатия бетона и поперечной арматуры и принимаемый равным:
- коэффициент, учитывающий влияние поперечного обжатия бетона и поперечной арматуры и принимаемый равным:
а) для крайних свободных опор,
#G0если 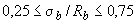
| - 0,75; |
если 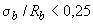 или или 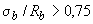
| - 1,0, |
здесь 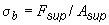 ;
;
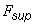 ,
, 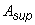 - опорная реакция и площадь опирания балки;
- опорная реакция и площадь опирания балки;
при этом если имеется поперечная арматура, охватывающая без приварки продольную арматуру, коэффициент 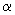 делится на величину
делится на величину 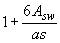 (где
(где 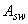 и
и 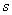 - площадь сечения огибающего хомута и его шаг) и принимается не менее 0,7;
- площадь сечения огибающего хомута и его шаг) и принимается не менее 0,7;
б) для свободных концов консоли - 1,0.
В любом случае коэффициент 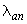 принимается не менее 15, а длина зоны анкеровки
принимается не менее 15, а длина зоны анкеровки 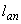 принимается не менее 200 мм.
принимается не менее 200 мм.
Для стержней диаметром менее 36 мм значение 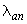 можно принимать по табл.3.3.
можно принимать по табл.3.3.
Таблица 3.3
| #G0Класс арматуры | Коэффициент 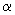
| Относительная длина анкеровки арматуры 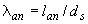 при бетоне классов при бетоне классов
| ||||||||||
| В10 | В15 | В20 | В25 | B30 | B35 | B40 | B45 | B50 | B55 | В60 | ||
| А240 | 0,7 | |||||||||||
| 0,75 | ||||||||||||
| 1,0 | ||||||||||||
| А300 | 0,7 | |||||||||||
| 0,75 | ||||||||||||
| 1,0 | ||||||||||||
| А400 | 0,7 | |||||||||||
| 0,75 | ||||||||||||
| 1,0 | ||||||||||||
| А500 | 0,7 | |||||||||||
| 0,75 | ||||||||||||
| 1,0 | ||||||||||||
| В500 | 0,7 | |||||||||||
| 0,75 | ||||||||||||
| 1,0 | ||||||||||||
Примечание. При расчете с учетом только постоянных и длительных нагрузок значения 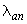 следует делить на следует делить на 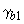 =0,9. =0,9.
|
В случае приваривания к продольным растянутым стержням поперечной или распределительной арматуры усилие 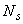 увеличивается на величину
увеличивается на величину
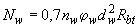 , (3.75)
, (3.75)
принимаемую не более 0,8 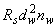 .
.
Здесь:
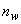 - количество приваренных стержней по длине
- количество приваренных стержней по длине 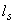 ;
;
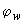 - коэффициент, принимаемый по табл.3.4;
- коэффициент, принимаемый по табл.3.4;
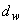 - диаметр привариваемых стержней.
- диаметр привариваемых стержней.
Таблица 3.4
#G0 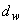
| |||||
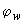
|
При этом значение 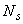 принимается не более значения, вычисленного по формуле (3.73) с использованием при определении
принимается не более значения, вычисленного по формуле (3.73) с использованием при определении 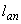 коэффициента
коэффициента 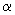 =0,7.
=0,7.
При устройстве на концах стержней специальных анкеров в виде пластин, шайб, гаек, уголков, высаженных головок и т.п., удовлетворяющих требованиям п.5.35, а также при приварке концов стержней к надежно заанкеренным закладным деталям усилие 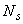 принимается равным
принимается равным 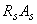 .
.
3.46. Для свободно опертых балок невыгоднейшее наклонное сечение начинается от грани опоры и имеет проекцию  , принимаемую не более
, принимаемую не более  и определяемую следующим образом:
и определяемую следующим образом:
а) если на элемент действуют сосредоточенные силы, значения  принимаются равными расстояниям от опоры до точек приложения этих сил, а также равным
принимаются равными расстояниям от опоры до точек приложения этих сил, а также равным 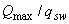 , если это значение меньше расстояния до 1-го груза;
, если это значение меньше расстояния до 1-го груза;
б) если на элемент действует равномерно распределенная нагрузка 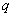 , значение
, значение  определяется по формуле:
определяется по формуле:
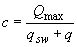 , (3.76)
, (3.76)
здесь 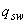 - см. формулу (3.48).
- см. формулу (3.48).
Если хомуты в пределах длины  меняют свою интенсивность с
меняют свою интенсивность с 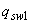 у начала наклонного сечения на
у начала наклонного сечения на 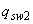 , значение
, значение  определяется по формуле (3.76) при уменьшении числителя на
определяется по формуле (3.76) при уменьшении числителя на 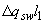 , а знаменателя - на
, а знаменателя - на 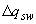 , (где
, (где 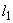 - длина участка с интенсивностью
- длина участка с интенсивностью 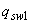 ,
, 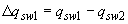 ).
).
Для балок с наклонной сжатой гранью при действии равномерно распределенной нагрузки проверяют наклонные сечения со значениями  , равными
, равными
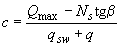 ,
, 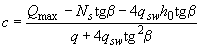 , (3.77)
, (3.77)
где 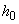 - рабочая высота в опорном сечении;
- рабочая высота в опорном сечении;
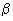 - угол наклона сжатой грани к горизонтали.
- угол наклона сжатой грани к горизонтали.
При растянутой грани, наклоненной под углом 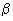 к горизонтали, в этих формулах значение
к горизонтали, в этих формулах значение 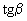 заменяется на
заменяется на 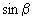 .
.
Для консолей, нагруженных сосредоточенными силами (черт.3.19, б), проверяются наклонные сечения, начинающиеся у мест приложения сосредоточенных сил вблизи свободного конца со значениями 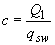 (где
(где 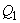 - поперечная сила в начале наклонного сечения), но не более
- поперечная сила в начале наклонного сечения), но не более 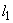 - расстояния от начала наклонного сечения до опоры. При этом, если
- расстояния от начала наклонного сечения до опоры. При этом, если 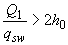 , следует принимать
, следует принимать 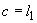 . Если такие консоли имеют наклонную сжатую грань, значение
. Если такие консоли имеют наклонную сжатую грань, значение 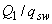 заменяется на
заменяется на 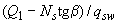 .
.
Для консолей, нагруженных только равномерно распределенной нагрузкой 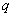 , невыгоднейшее сечение заканчивается в опорном сечении и имеет длину проекции
, невыгоднейшее сечение заканчивается в опорном сечении и имеет длину проекции
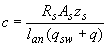 , (3.78)
, (3.78)
но не более  .
.
В случае, если 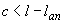 , расчет наклонного сечения можно не производить.
, расчет наклонного сечения можно не производить.
Здесь:  - площадь сечения арматуры, доводимой до свободного конца;
- площадь сечения арматуры, доводимой до свободного конца; 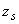 - см. п.3.43;
- см. п.3.43; 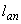 - см. п.3.45.
- см. п.3.45.
При отсутствии поперечной арматуры значение  принимают равным
принимают равным  , где
, где 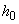 - рабочая высота в конце наклонного сечения.
- рабочая высота в конце наклонного сечения.
3.47. Для обеспечения прочности наклонных сечений на действие момента в элементах постоянной высоты с хомутами продольные растянутые стержни, обрываемые в пролете, должны заводиться за точку теоретического обрыва (т.е. за нормальное сечение, в котором внешний момент становится равным предельному моменту 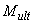 без учета обрываемой арматуры, черт.3.20) на длину не менее величины
без учета обрываемой арматуры, черт.3.20) на длину не менее величины 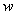 , определяемой по формуле
, определяемой по формуле
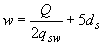 ; (3.79)
; (3.79)
при этом, если
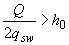 ,
, 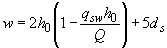 , (3.80)
, (3.80)
где 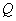 - поперечная сила в нормальном сечении, проходящем через точку теоретического обрыва;
- поперечная сила в нормальном сечении, проходящем через точку теоретического обрыва;
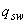 - см. п.3.31;
- см. п.3.31;
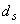 - диаметр обрываемого стержня.
- диаметр обрываемого стержня.
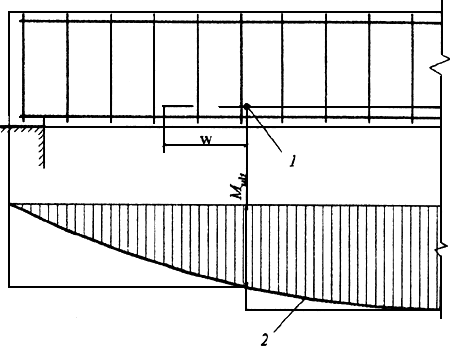
Черт.3.20. Обрыв растянутых стержней в пролете
1 - точка теоретического обрыва; 2 - эпюра 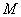
Для балки с наклонной сжатой гранью при 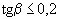 величина
величина 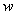 принимается равной
принимается равной
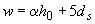 , (3.81)
, (3.81)
при этом, если
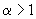 ,
, 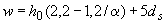 , (3.82)
, (3.82)
где 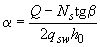 ,
,
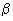 - угол наклона грани к горизонтали.
- угол наклона грани к горизонтали.
Для балки с наклонной растянутой гранью 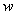 определяется аналогично с заменой
определяется аналогично с заменой 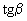 на
на 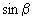 .
.
Для элементов без поперечной арматуры значение 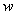 принимают равным
принимают равным  .
.
Кроме того, должны быть учтены требования пп.5.32 и 5.33.
3.48. Для обеспечения прочности наклонных сечений на действие момента начало отгиба в растянутой зоне должно отстоять от нормального сечения, в котором отгибаемый стержень полностью используется по моменту, не менее, чем на 0,5 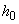 , а конец отгиба должен быть расположен не ближе того нормального сечения, в котором отгиб не требуется по расчету (черт.3.21).
, а конец отгиба должен быть расположен не ближе того нормального сечения, в котором отгиб не требуется по расчету (черт.3.21).
Черт.3.21. К определению места отгиба продольной растянутой арматуры
Примеры расчета
Расчет наклонных сечений на действие поперечных сил
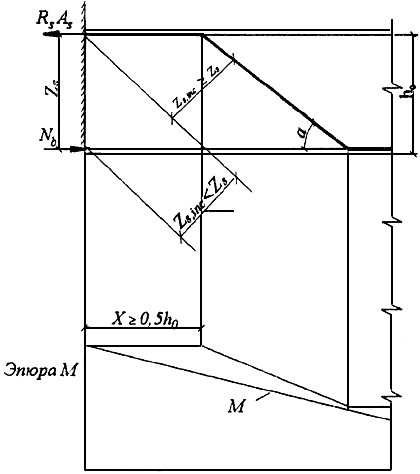
Пример 12. Дано: ребро ТТ-образной плиты перекрытия с размерами сечения: 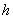 =350 мм,
=350 мм, 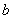 =85 мм;
=85 мм; 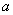 =35 мм; бетон класса В15 (
=35 мм; бетон класса В15 ( 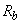 =8,5 МПа,
=8,5 МПа, 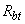 =0,75 МПа); ребро армировано плоским каркасом с поперечными стержнями из арматуры класса А400 (
=0,75 МПа); ребро армировано плоским каркасом с поперечными стержнями из арматуры класса А400 ( 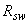 =285 МПа) диаметром 8 мм (
=285 МПа) диаметром 8 мм ( 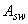 =50,3 мм
=50,3 мм  ) шагом
) шагом 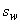 =100 мм; полная равномерно распределенная нагрузка, действующая на ребро,
=100 мм; полная равномерно распределенная нагрузка, действующая на ребро, 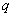 =21,9 кН/м; временная эквивалентная нагрузка
=21,9 кН/м; временная эквивалентная нагрузка 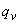 =18 кН/м; поперечная сила на опоре
=18 кН/м; поперечная сила на опоре 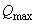 =62 кН.
=62 кН.
Требуется проверить прочность наклонных сечений и бетонной полосы между наклонными сечениями.
Расчет. 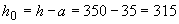 мм.
мм.
Прочность бетонной полосы проверим из условия (3.43):
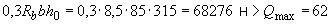 кН,
кН,
т.е. прочность полосы обеспечена.
Прочность наклонного сечения по поперечной силе проверим согласно п.3.31.
По формуле (3.48) определим интенсивность хомутов
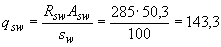 Н/мм.
Н/мм.
Поскольку 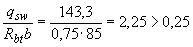 , т.е. условие (3.49) выполнено, хомуты полностью учитываем и значение
, т.е. условие (3.49) выполнено, хомуты полностью учитываем и значение 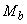 определяем по формуле (3.46)
определяем по формуле (3.46)
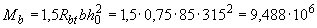 Н·мм.
Н·мм.
Согласно п.3.32 определим длину проекции невыгоднейшего наклонного сечения  .
.
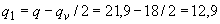 кН/м (Н/мм).
кН/м (Н/мм).
Поскольку 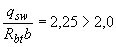 , значение
, значение  определяем по формуле
определяем по формуле
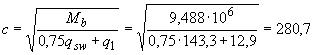 мм
мм 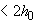 .
.
Принимаем 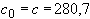 мм. Тогда
мм. Тогда
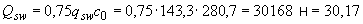 кН.
кН.
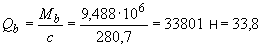 кН.
кН.
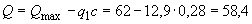 кН.
кН.
Проверяем условие (3.44)
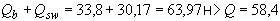 кН,
кН,
т.е. прочность наклонных сечений обеспечена.
Проверим требование п.3.35:
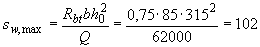 мм
мм 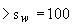 мм,
мм,
т.е. требование выполнено. Условия п.5.21 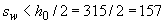 мм и
мм и 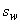 <300 мм также выполнены.
<300 мм также выполнены.
Пример 13. Дано: свободно опертая балка перекрытия с размерами сечения: 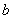 =200 мм,
=200 мм, 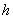 =400 мм;
=400 мм; 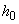 =370 мм; бетон класса В25 (
=370 мм; бетон класса В25 ( 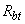 =1,05 МПа); хомуты двухветвевые диаметром 8 мм (
=1,05 МПа); хомуты двухветвевые диаметром 8 мм ( 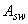 =101 мм
=101 мм  ) с шагом
) с шагом 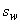 =150 мм; арматура класса А240 (
=150 мм; арматура класса А240 ( 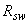 =170 МПа); временная эквивалентная по моменту нагрузка
=170 МПа); временная эквивалентная по моменту нагрузка 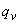 =36 кН/м, постоянная нагрузка
=36 кН/м, постоянная нагрузка 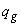 =14 кН/м; поперечная сила на опоре
=14 кН/м; поперечная сила на опоре 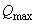 =137,5 кН.
=137,5 кН.
Дата добавления: 2017-02-20; просмотров: 887;
