Расчет железобетонных элементов по наклонным сечениям на действие поперечных сил 1 страница

Элементы постоянной высоты, армированные хомутами, нормальными к оси элемента

3.31. Расчет изгибаемых элементов по наклонному сечению (черт.3.9) производят из условия

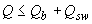, (3.44)

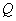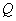где - поперечная сила в наклонном сечении с длиной проекции от внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения; при вертикальной нагрузке, приложенной к верхней грани элемента, значение принимается в нормальном сечении, проходящем на расстоянии от опоры; при этом следует учитывать возможность отсутствия временной нагрузки на приопорном участке длиной ;

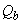- поперечная сила, воспринимаемая бетоном в наклонном сечении;

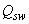- поперечная сила, воспринимаемая хомутами в наклонном сечении.

Черт.3.9. Схема усилий в наклонном сечении элементов с хомутами при расчете его на действие поперечной силы

Поперечную силу 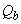определяют по формуле

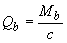, (3.45)

где

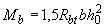. (3.46)

Значение 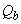принимают не более 2,5 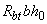и не менее 0,5 .

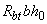Значение определяют согласно п.3.32.

Усилие 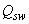определяют по формуле

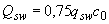, (3.47)

где 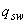- усилие в хомутах на единицу длины элемента, равное

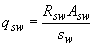, (3.48)

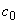- длина проекции наклонной трещины, принимаемая равной , но не более .

Хомуты учитывают в расчете, если соблюдается условие

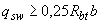. (3.49)

Можно не выполнять это условие, если в формуле (3.46) учитывать такое уменьшенное значение 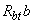, при котором условие (3.49) превращается в равенство, т.е. принимать .

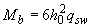3.32. При проверке условия (3.44) в общем случае задаются рядом наклонных сечений при различных значениях , не превышающих расстояние от опоры до сечения с максимальным изгибающим моментом и не более .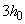

При действии на элемент сосредоточенных сил значения принимают равными расстояниям от опоры до точек приложения этих сил (черт.3.10), а также равными 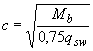, но не меньше 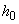, если это значение меньше расстояния от опоры до 1-го груза.

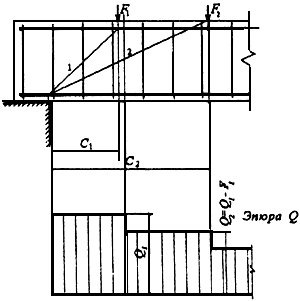
Черт.3.10. Расположение расчетных наклонных сечений при сосредоточенных силах

1 - наклонное сечение, проверяемое на действие поперечной силы ;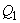

2 - то же, силы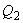

При расчете элемента на действие равномерно распределенной нагрузки 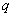невыгоднейшее значение принимают равным 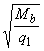, а если при этом 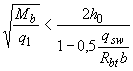или 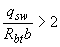, следует принимать 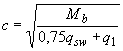, где значение 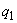определяют следующим образом:

а) если действует сплошная равномерно распределенная нагрузка , ;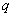

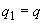б) если нагрузка 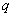включает в себя временную нагрузку, которая приводится к эквивалентной по моменту равномерно распределенной нагрузке 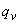(т.е. когда эпюра моментов 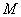от принятой в расчете нагрузки 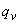всегда огибает эпюру 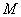от любой фактической временной нагрузки), .

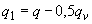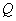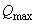При этом в условии (3.44) значение принимают равным , где - поперечная сила в опорном сечении.

3.33. Требуемая интенсивность хомутов, выражаемая через 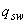(см. п.3.31), определяется следующим образом:

а) при действии на элемент сосредоточенных сил, располагаемых на расстояниях 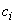от опоры, для каждого 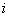-го наклонного сечения с длиной проекции 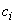, не превышающей расстояния до сечения с максимальным изгибающим моментом, значение 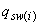определяется следующим образом в зависимости от коэффициента 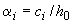, принимаемого не более 3:

если

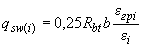, ; (3.50)

если

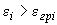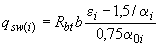, , (3.51)

где 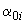- меньшее из значений 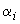и 2;

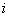- поперечная сила в -ом нормальном сечении, расположенном на расстоянии 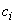от опоры;

окончательно принимается наибольшее значение ;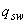

б) при действии на элемент только равномерно распределенной нагрузки 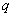требуемая интенсивность хомутов 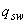определяется в зависимости от 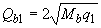следующим образом:

если ,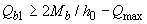

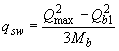; (3.52)

если ,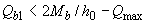

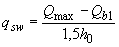; (3.53)

при этом, если

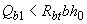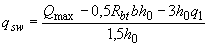, , (3.54)

где 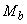- см. п.3.31; 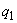- см. п.3.32.

В случае, если полученное значение 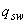не удовлетворяет условию (3.49), его следует вычислять по формуле

(3.55)

и принимать не менее .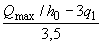

3.34. При уменьшении интенсивности хомутов от опоры к пролету с 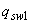до 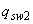(например, увеличением шага хомутов) следует проверить условие (3.44) при значениях , превышающих 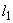- длину участка с интенсивностью хомутов 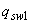(черт.3.11). При этом значение 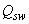принимается равным:

если

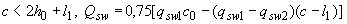; (3.56)

если

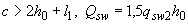, (3.57)

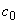- см. п.3.31.

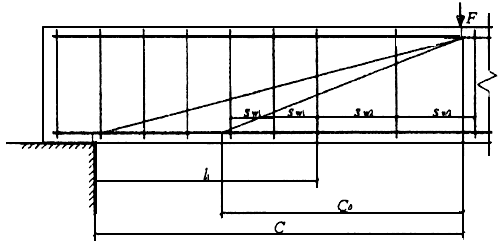
Черт.3.11. К расчету наклонных сечений при изменении интенсивности хомутов

При действии на элемент равномерно распределенной нагрузки длина участка с интенсивностью хомутов 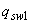принимается не менее значения 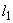, определяемого в зависимости от 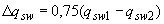следующим образом:

- если ,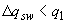

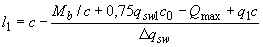, (3.58)

где 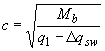, но не более ,

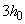при этом, если , ;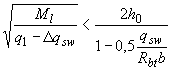

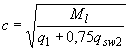- если ,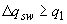

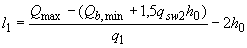; (3.59)

здесь 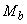, 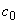- см. п.3.31; 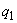- см. п.3.32;

.

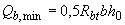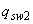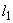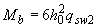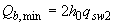Если для значения не выполняется условие (3.49), длина вычисляется при скорректированных согласно п.3.31 значениях и ; при этом сумма ( 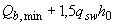) в формуле (3.59) принимается не менее нескорректированного значения .

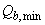3.35. Шаг хомутов, учитываемых в расчете, должен быть не более значения:

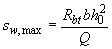. (3.60)

Кроме того, хомуты должны отвечать конструктивным требованиям, приведенным в пп.5.20 и 5.21.

Элементы переменной высоты с поперечным армированием

3.36. Расчет элементов с наклонными на приопорных участках сжатыми или растянутыми гранями производят согласно п.3.31, принимая в качестве рабочей высоты сечения наибольшее значение 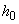в пределах рассматриваемого наклонного сечения (черт.3.12).

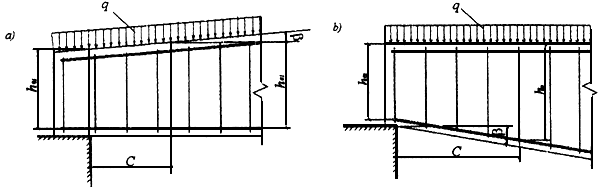
Черт.3.12 Балки с переменной высотой сечения и наклонной гранью

3.37. Для балок без отгибов высотой, равномерно увеличивающейся от опоры к пролету, рассчитываемых на действие равномерно распределенной нагрузки 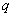, наклонное сечение проверяют из условия (3.44) при невыгоднейшем значении , равном

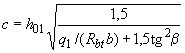, (3.61)

при этом, если это значение меньше 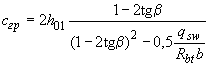или, если 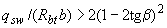, то невыгоднейшее значение равно

. (3.62)

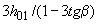Принятое значение не должно превышать , а также длину участка балки с постоянным значением .

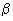Здесь: 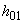- рабочая высота опорного сечения балки;

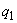- см. п.3.32;

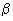- угол между сжатой и растянутой гранями балки.

Рабочую высоту принимают равной .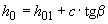

При уменьшении интенсивности хомутов от 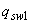у опоры до 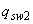в пролете следует проверить условие (3.44) при значениях , превышающих 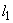- длину участка элемента с интенсивностью хомутов 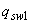; при этом значение 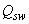определяют по формуле (3.56) либо по формуле (3.57) п.3.34 в зависимости от выполнения или невыполнения условия .

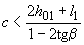При действии на балку сосредоточенных сил, значение принимают равным расстоянию от опоры до точек приложения этих сил, а также определяют по формуле (3.62) при 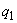=0, если это значение меньше расстояния от опоры до 1-го груза.

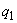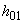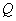3.38. Для консолей без отгибов высотой, равномерно увеличивающейся от свободного конца к опоре (черт.3.13), в общем случае проверяют условие (3.44), задаваясь наклонными сечениями со значениями , определяемыми по формуле (3.62) при =0 и принимаемыми не более расстояния от начала наклонного сечения в растянутой зоне до опоры. При этом за и принимают соответственно рабочую высоту и поперечную силу в начале наклонного сечения в растянутой зоне. Кроме того, если 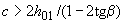, проверяют наклонные сечения, проведенные до опоры.

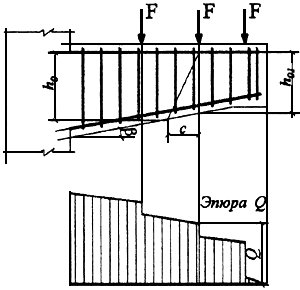
Черт.3.13. Консоль высотой, уменьшающейся от опоры к свободному концу

При действии на консоль сосредоточенных сил начало наклонного сечения располагают в растянутой зоне нормальных сечений, проведенных через точки приложения этих сил (см. черт.3.13).

При действии равномерно распределенной нагрузки или нагрузки, линейно увеличивающейся к опоре, консоль рассчитывают как элемент с постоянной высотой сечения согласно пп.3.31 и 3.32, принимая рабочую высоту 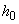в опорном сечении.

Элементы, армированные отгибами

3.39. Проверку прочности наклонного сечения на действие поперечной силы для элемента с отгибами производят из условия (3.44) с добавлением к правой его части значения

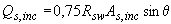, (3.63)

где 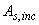- площадь сечения отгибов, пересекающих наклонную трещину, расположенную у конца наклонного сечения с длиной проекции равной , но не более (черт.3.14);

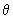- угол наклона отгибов к продольной оси элемента.

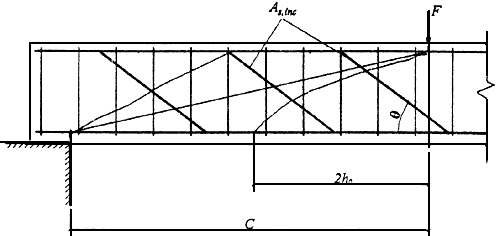
Черт.3.14. К определению наиболее опасной наклонной трещины для элементов с отгибами при расчете на действие поперечной силы

Значения принимают равным расстояниям от опоры до концов отгибов, а также до мест приложения сосредоточенных сил; кроме того, следует проверить наклонные сечения, заканчивающиеся на расстоянии от начала предпоследней и последней плоскости отгибов (черт.3.15).

Черт.3.15. К определению наклонных сечений в элементе с отгибами

1-4 - расчетные наклонные сечения

3.40. Расстояния между опорой и концом отгиба, ближайшего к опоре 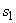, а также между концом предыдущей и началом последующего* отгибов 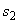(черт.3.16) должно быть не более .

________________

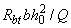* Текст соответствует оригиналу. - Примечание "КОДЕКС".

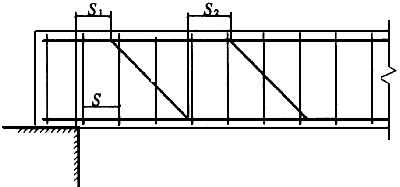
Черт.3.16. Расстояния между хомутами, опорой и отгибами

Кроме того, отгибы должны удовлетворять конструктивным требованиям, приведенным в п.5.22.

Элементы без поперечной арматуры

3.41. Расчет элементов без поперечной арматуры на действие поперечной силы производится из условий

а)

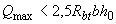; (3.64)

где 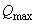- максимальная поперечная сила у грани опоры;

б)

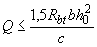, (3.65)

где 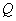- поперечная сила в конце наклонного сечения, начинающегося от опоры; значение принимается не более .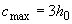

Для сплошных плоских плит с несвободными краями (соединенными с другими элементами или имеющими опоры) и шириной 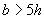допускается принимать .

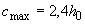При действии на элемент сосредоточенных сил значения принимаются равными расстояниям от опоры до точек приложения этих сил (черт.3.17), но не более .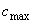

Черт.3.17. Расположение невыгоднейших наклонных сечений в элементах без поперечной арматуры

1 - наклонное сечение, проверяемое на действие поперечной силы 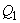; 2 - то же, силы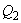

При расчете элемента на действие распределенных нагрузок, если выполняется условие

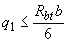, (3.66)

условие (3.65) принимает вид

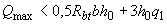(3.67)

(что соответствует ),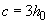

а при невыполнении условия (3.66) -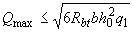

(что соответствует ).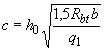

Для упомянутых плоских плит с несвободными боковыми краями правая часть условия (3.66) делится на 0,64, а условие (3.67) принимает вид

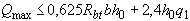. (3.67a)

Здесь 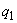принимается при действии равномерно распределенной нагрузки в соответствии с п.3.32, а при действии сплошной нагрузки с линейно изменяющейся интенсивностью - равной средней интенсивности на приопорном участке длиной, равной четверти пролета балки (плиты) или половины вылета консоли, но не более .

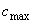3.42. Для элементов с переменной высотой сечения при проверке условия (3.64) значение 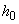принимается в опорном сечении, а при проверке условия (3.65) - как среднее значение 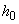в пределах наклонного сечения.

Для элементов с высотой сечения, увеличивающейся с увеличением поперечной силы, значение 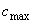принимается равным 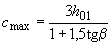, а для плоских плит, указанных в п.3.41, - ,

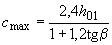где 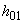- рабочая высота в опорном сечении;

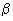- угол между растянутой и сжатой гранями.

При действии на такой элемент распределенной нагрузки значение в условии (3.65) принимается равным

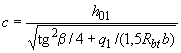, (3.68)

но не боле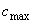е , где 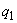- см. п.3.32.

Расчет железобетонных элементов по наклонным сечениям на действие моментов

3.43. Расчет железобетонных элементов по наклонным сечениям на действие момента (черт.3.18) производят из условия

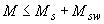, (3.69)

где 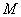- момент в наклонном сечении с длиной проекции на продольную ось элемента, определяемый от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения, относительно конца наклонного сечения (точка 0), противоположного концу, у которого располагается проверяемая продольная арматура, испытывающая растяжение от момента в наклонном сечении (черт. 3.19)