Расчет железобетонных элементов по наклонным сечениям на действие поперечных сил 4 страница
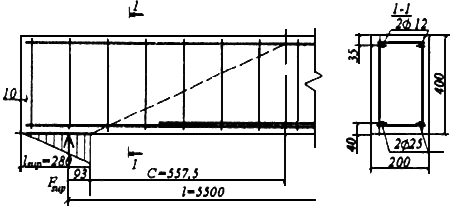
Черт.3.25. К примеру расчета 20
Требуется проверить прочность наклонных сечений на действие момента.
Расчет. 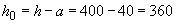 мм. Поскольку растянутая арматура не имеет анкеров, расчет наклонных сечений на действие момента необходим.
мм. Поскольку растянутая арматура не имеет анкеров, расчет наклонных сечений на действие момента необходим.
Определим усилие в растянутой арматуре по формуле (3.73).
Принимаем начало наклонного сечения у грани опоры. Отсюда 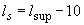 мм
мм 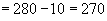 мм (см. черт.3.25).
мм (см. черт.3.25).
Опорная реакция балки равна
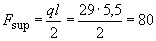 кН,
кН,
а площадь опирания балки 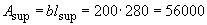 мм
мм  ,
,
откуда 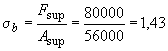 МПа,
МПа, 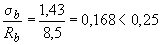 ,
,
следовательно, 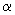 =1,0. Из табл.3.3 при классе бетона В15, классе арматуры А400 и
=1,0. Из табл.3.3 при классе бетона В15, классе арматуры А400 и 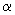 =1,0 находим
=1,0 находим 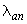 =47. Тогда, длина анкеровки равна
=47. Тогда, длина анкеровки равна 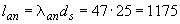 мм.
мм.
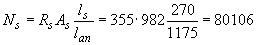 Н.
Н.
Поскольку к растянутым стержням в пределах длины 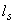 приварены 4 вертикальных и 2 горизонтальных поперечных стержня (см. черт.3.25), увеличим усилия
приварены 4 вертикальных и 2 горизонтальных поперечных стержня (см. черт.3.25), увеличим усилия 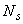 на величину
на величину 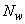 .
.
Принимая 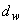 =8 мм,
=8 мм, 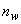 =6,
=6, 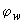 =150 (см. табл.3.4), получаем
=150 (см. табл.3.4), получаем
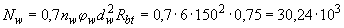 H.
H.
Отсюда 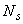 =80106+30240=110346 H.
=80106+30240=110346 H.
Определяем максимально допустимое значение 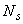 . Из табл.3.3 при
. Из табл.3.3 при 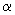 =0,7 находим
=0,7 находим 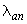 =33; тогда
=33; тогда
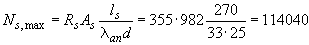 Н
Н 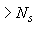 , т.е. оставляем
, т.е. оставляем 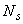 =110346 H.
=110346 H.
Определим плечо внутренней пары сил
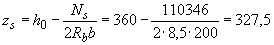 мм
мм 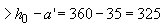 мм.
мм.
Тогда момент, воспринимаемый продольной арматурой, равен
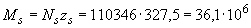 Н·мм.
Н·мм.
По формуле (3.48) вычислим величину 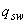
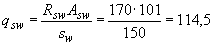 Н·мм.
Н·мм.
Определяем длину проекции невыгоднейшего наклонного сечения по формуле (3.76), принимая значение 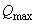 равным опорной реакции балки, т.е.
равным опорной реакции балки, т.е. 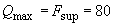 кН.
кН.
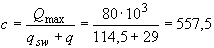 мм
мм 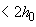 .
.
Тогда момент, воспринимаемый поперечной арматурой, равен
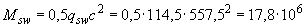 Н·мм.
Н·мм.
Момент в наклонном сечении определяем как момент в нормальном сечении, расположенном в конце наклонного сечения, т.е. на расстоянии от точки приложения опорной реакции, равной 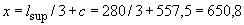 мм
мм
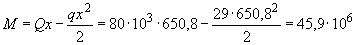 Н·мм
Н·мм 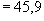 кН·м.
кН·м.
Проверяем условие (3.69)
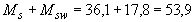 кН·м
кН·м 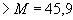 кН·м,
кН·м,
т.е. прочность наклонных сечений по изгибающему моменту обеспечена.
Пример 21. Дано: ригель многоэтажной рамы с эпюрами моментов и поперечных сил от равномерно распределенной нагрузки 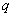 =228 кН/м по черт.3.26; бетон класса В25; продольная и поперечная арматура класса А400 (
=228 кН/м по черт.3.26; бетон класса В25; продольная и поперечная арматура класса А400 ( 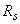 =355 МПа,
=355 МПа, 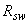 =285 МПа); поперечное сечение приопорного участка - по черт.3.26; хомуты трехветвевые диаметром 10 мм (
=285 МПа); поперечное сечение приопорного участка - по черт.3.26; хомуты трехветвевые диаметром 10 мм ( 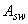 =236 мм
=236 мм  ) шагом
) шагом 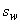 равным 150 мм.
равным 150 мм.
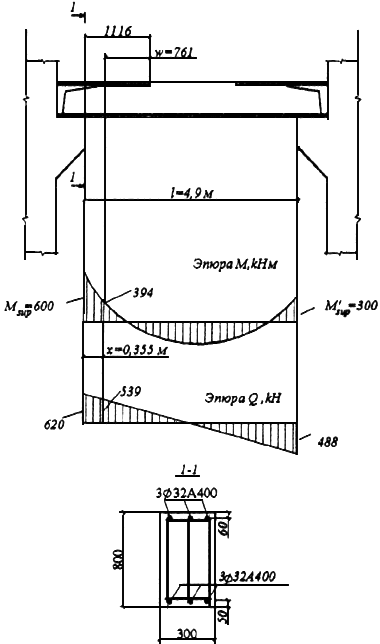
Черт.3.26. К примеру расчета 21
Требуется определить расстояние от левой опоры до места обрыва первого стержня верхней арматуры.
Расчет. Из черт.3.26 имеем: 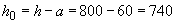 мм;
мм; 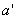 =50 мм; площадь сечения верхней растянутой арматуры без учета одного обрываемого стержня
=50 мм; площадь сечения верхней растянутой арматуры без учета одного обрываемого стержня  32
32  =1609 мм
=1609 мм  (2
(2 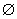 32);
32); 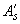 =2413 мм
=2413 мм  (3
(3 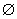 32). Определим предельный момент, соответствующий этой арматуре по формуле (3.19), поскольку
32). Определим предельный момент, соответствующий этой арматуре по формуле (3.19), поскольку 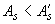 , т.е.
, т.е. 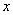 <0:
<0:
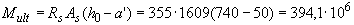 Н·мм
Н·мм 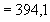 кН·м.
кН·м.
По эпюре моментов определяем расстояние от опоры до места теоретического обрыва первого стержня из уравнения
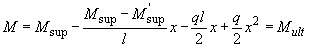 ,
,
откуда 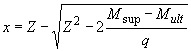 , где
, где 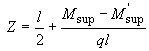 ;
;
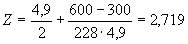 м;
м; 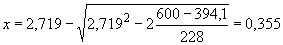 м.
м.
Поперечная сила в месте теоретического обрыва равна
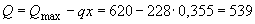 кН.
кН.
Определим величину 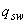
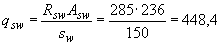 Н/мм.
Н/мм.
Поскольку 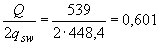 м
м 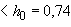 м, длину
м, длину 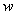 , на которую надо завести обрываемый стержень за точку теоретического обрыва, определяем по формуле (3.79)
, на которую надо завести обрываемый стержень за точку теоретического обрыва, определяем по формуле (3.79)
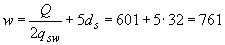 мм.
мм.
Следовательно, расстояние от опоры до места обрыва стержня может быть принято равным 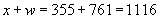 мм.
мм.
Определим необходимое расстояние 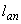 от места обрыва стержня до опорного сечения, предполагая полное использование этого стержня в опорном сечении. Для этого по табл.3.3 при
от места обрыва стержня до опорного сечения, предполагая полное использование этого стержня в опорном сечении. Для этого по табл.3.3 при 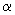 =1,0 классе бетона В25, классе арматуры А400 находим
=1,0 классе бетона В25, классе арматуры А400 находим 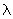 =34. Тогда
=34. Тогда 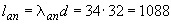 мм
мм 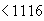 мм.
мм.
Следовательно, обрываем стержень на расстоянии 1116 мм от опоры.
ВНЕЦЕНТРЕННО СЖАТЫЕ ЭЛЕМЕНТЫ
ОБЩИЕ ПОЛОЖЕНИЯ
3.49. При расчете железобетонных элементов на действие сжимающей продольной силы следует учитывать случайный эксцентриситет 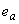 принимаемый не менее:
принимаемый не менее:
1/600 длины элемента или расстояния между его сечениями, закрепленными от смещения;
1/30 высоты сечения;
10 мм.
Для элементов статически неопределимых конструкций (в том числе для колонн каркасных зданий) значение эксцентриситета продольной силы относительно центра тяжести приведенного сечения 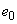 принимают равным значению эксцентриситета, полученного из статического расчета, но не менее
принимают равным значению эксцентриситета, полученного из статического расчета, но не менее 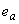 .
.
Для элементов статически определимых конструкций (например, фахверковые стойки, стойки ЛЭП и т.п.) эксцентриситет 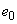 принимают равным сумме эксцентриситетов - из статического расчета конструкции и случайного.
принимают равным сумме эксцентриситетов - из статического расчета конструкции и случайного.
3.50. Расчет нормальных сечений внецентренно сжатых элементов производят в плоскости эксцентриситета продольной силы (в плоскости изгиба) и отдельно в нормальной к ней плоскости с эксцентриситетом 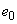 , равным случайному
, равным случайному 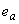 (см. п.3.49).
(см. п.3.49).
Расчет из плоскости изгиба можно не производить, если гибкость элемента 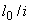 (для прямоугольных сечений -
(для прямоугольных сечений - 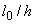 ) в плоскости изгиба превышает гибкость в плоскости, нормальной плоскости изгиба.
) в плоскости изгиба превышает гибкость в плоскости, нормальной плоскости изгиба.
Расчет элемента с учетом эксцентриситетов в плоскостях обеих главных осей (косое внецентренное сжатие) следует производить, если оба эти эксцентриситета превышают случайные 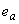 .
.
Во всех случаях эксцентриситеты 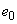 определяются с учетом влияния прогиба элемента (см. пп.3.53-3.55).
определяются с учетом влияния прогиба элемента (см. пп.3.53-3.55).
3.51. Расчет нормальных сечений внецентренно сжатых элементов в общем случае производят на основе нелинейной деформационной модели согласно пп.3.72-3.76.
Расчет элементов прямоугольного, таврового и двутаврового сечений с арматурой, расположенной у перпендикулярных плоскости изгиба граней элемента, при направлении эксцентриситета в плоскости симметрии сечения допускается производить по предельным усилиям согласно пп.3.56-3.61.
Кроме того, по предельным усилиям можно производить расчет:
- элементов кольцевого и круглого сечений с арматурой, равномерно распределенной по окружности, при числе стержней более 6 согласно пп.3.62-3.65;
- элементов прямоугольного сечения с арматурой в виде 4-х одинаковых угловых стержней на косое внецентренное сжатие согласно п.3.66.
РАСЧЕТ ПРИ ДЕЙСТВИИ ПОПЕРЕЧНЫХ СИЛ
3.52. Расчет внецентренно сжатых элементов при действии поперечных сил производится аналогично расчету изгибаемых элементов в соответствии с пп.3.29-3.35 и следующих указаний:
а) при 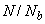 >0,5 правая часть условия (3.43) умножается на коэффициент
>0,5 правая часть условия (3.43) умножается на коэффициент
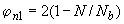 , (3.83)
, (3.83)
где 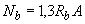 , но не менее
, но не менее 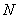 ;
;
б) значение поперечной силы, воспринимаемой бетоном в наклонном сечении 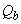 , а также правая часть условия (3.49) умножается на коэффициент
, а также правая часть условия (3.49) умножается на коэффициент
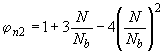 ; (3.84)
; (3.84)
на этот коэффициент 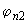 умножается также связанное с
умножается также связанное с 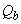 значение
значение 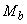 .
.
УЧЕТ ВЛИЯНИЯ ПРОГИБА ЭЛЕМЕНТОВ
3.53. Влияние прогиба элемента на момент продольной силы (или ее эксцентриситет 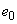 ) учитывается, как правило, путем расчета конструкции по деформированной схеме, принимая во внимание неупругие деформации бетона и арматуры, а также наличие трещин.
) учитывается, как правило, путем расчета конструкции по деформированной схеме, принимая во внимание неупругие деформации бетона и арматуры, а также наличие трещин.
Допускается производить расчет конструкции по недеформированной схеме, а влияние прогиба элемента учитывать путем умножения моментов на коэффициенты 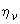 и
и 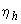 в соответствии с формулой
в соответствии с формулой
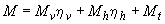 , (3.85)
, (3.85)
где 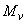 - момент от вертикальных нагрузок, не вызывающих заметных горизонтальных смещений концов;
- момент от вертикальных нагрузок, не вызывающих заметных горизонтальных смещений концов;
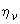 - коэффициент, принимаемый равным:
- коэффициент, принимаемый равным:
для сечений в концах элемента: при податливой заделке - 1,0; при жесткой заделке - по формуле (3.86);
для сечений в средней трети длины элемента - по формуле (3.86);
для прочих сечений - по линейной интерполяции;
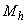 - момент от нагрузок, вызывающих горизонтальное смещение концов (ветровых и т.п.);
- момент от нагрузок, вызывающих горизонтальное смещение концов (ветровых и т.п.);
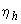 - коэффициент, определяемый по формуле (3.86);
- коэффициент, определяемый по формуле (3.86);
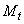 - момент от вынужденных горизонтальных смещений концов (т.е. смещений, не зависящих от жесткости элемента, например, от температурных деформаций перекрытий и т.п.).
- момент от вынужденных горизонтальных смещений концов (т.е. смещений, не зависящих от жесткости элемента, например, от температурных деформаций перекрытий и т.п.).
Моменты, используемые в настоящем пункте, допускается определять относительно центра тяжести бетонного сечения.
Примечание. Если вертикальные нагрузки вызывают заметные горизонтальные смещения (например при несимметричных рамах), то моменты 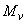 определяются при фиктивных горизонтальных неподвижных опорах, а моменты от горизонтальных сил, равных реакциям в этих опорах, следует относить к моментам
определяются при фиктивных горизонтальных неподвижных опорах, а моменты от горизонтальных сил, равных реакциям в этих опорах, следует относить к моментам 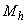 , т.е. суммировать с моментами от горизонтальных нагрузок.
, т.е. суммировать с моментами от горизонтальных нагрузок.
3.54. Значение коэффициента 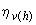 при расчете конструкции по недеформированной схеме определяется по формуле
при расчете конструкции по недеформированной схеме определяется по формуле
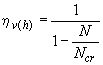 , (3.86)
, (3.86)
где 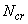 - условная критическая сила, определяемая по формуле
- условная критическая сила, определяемая по формуле
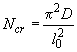 ; (3.87)
; (3.87)
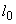 - расчетная длина элемента, определяемая для коэффициентов
- расчетная длина элемента, определяемая для коэффициентов 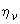 и
и 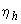 согласно соответственно п.3.55, а и п.3.55, б;
согласно соответственно п.3.55, а и п.3.55, б;
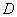 - жесткость железобетонного элемента в предельной стадии, определяемая по формулам:
- жесткость железобетонного элемента в предельной стадии, определяемая по формулам:
для элементов любой формы сечения
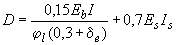 ; (3.88)
; (3.88)
для элементов прямоугольного сечения с арматурой, расположенной у наиболее сжатой и у растянутой (менее сжатой) грани элемента
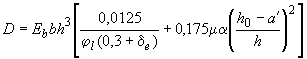 . (3.89)
. (3.89)
В формулах (3.88) и (3.89):
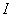 и
и 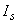 - момент инерции соответственно бетонного сечения и сечения всей арматуры относительно центра тяжести бетонного сечения;
- момент инерции соответственно бетонного сечения и сечения всей арматуры относительно центра тяжести бетонного сечения;
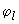 - коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента и равный
- коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента и равный
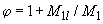 (3.90)
(3.90)
но не более 2;
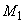 и
и 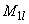 - моменты внешних сил относительно оси, нормальной плоскости изгиба и проходящей через центр наиболее растянутого или наименее сжатого (при целиком сжатом сечении) стержня арматуры, соответственно от действия всех нагрузок и от действия постоянных и длительных нагрузок; для элементов, рассчитываемых согласно пп.3.56-3.61, допускается
- моменты внешних сил относительно оси, нормальной плоскости изгиба и проходящей через центр наиболее растянутого или наименее сжатого (при целиком сжатом сечении) стержня арматуры, соответственно от действия всех нагрузок и от действия постоянных и длительных нагрузок; для элементов, рассчитываемых согласно пп.3.56-3.61, допускается 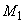 и
и 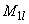 определять относительно оси, проходящей через центр тяжести всей арматуры
определять относительно оси, проходящей через центр тяжести всей арматуры 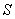 ;
;
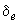 - коэффициент, принимаемый равным
- коэффициент, принимаемый равным 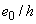 , но не менее 0,15 (для кольцевых и круглых сечений значение
, но не менее 0,15 (для кольцевых и круглых сечений значение 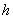 заменяется на
заменяется на 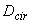 );
);
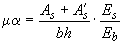 .
.
Жесткость 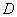 при вычислении коэффициентов
при вычислении коэффициентов 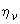 и
и 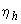 определяется с учетом всех нагрузок. В случае необходимости коэффициент
определяется с учетом всех нагрузок. В случае необходимости коэффициент 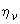 можно снизить, вычисляя жесткость
можно снизить, вычисляя жесткость 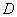 без учета нагрузок, вызывающих смещение концов.
без учета нагрузок, вызывающих смещение концов.
При гибкости элемента 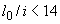 (для прямоугольных сечений - при
(для прямоугольных сечений - при 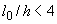 ) можно принимать
) можно принимать 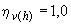 .
.
При 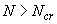 следует увеличивать размеры сечения.
следует увеличивать размеры сечения.
3.55. Расчетная длина 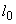 принимается равной:
принимается равной:
а) при вычислении коэффициента 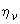 , а также при расчете элемента на действие продольной силы со случайным эксцентриситетом для элементов:
, а также при расчете элемента на действие продольной силы со случайным эксцентриситетом для элементов:
с шарнирным опиранием на двух концах - 1,0 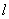 ;
;
с шарнирным опиранием на одном конце, а на другом конце:
с жесткой заделкой - 0,7 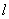
с податливой заделкой - 0,9 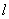 ;
;
с заделкой на двух концах: жесткой - 0,5 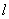 ;
;
податливой - 0,8 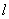 ;
;
с податливой заделкой на одном конце и с жесткой заделкой на другом - 0,7 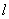 ;
;
б) при вычислении коэффициента 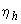 для элементов:
для элементов:
с шарнирным опиранием на одном конце, а на другом конце
с жесткой заделкой - 1,5 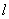 ;
;
с податливой заделкой -2,0 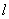 ;
;
с заделкой на двух концах: жесткой - 0,8 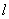 ;
;
податливой - 1,2 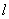 ;
;
с податливой заделкой на одном конце и с жесткой заделкой на другом - 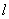 ;
;
с жесткой заделкой на одном конце и незакрепленным другим концом (консоль) -2 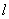 .
.
Здесь 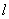 - расстояние между концами элемента.
- расстояние между концами элемента.
Для конкретных конструкций и сооружений можно принимать иные значения 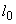 .
.
РАСЧЕТ НОРМАЛЬНЫХ СЕЧЕНИЙ ПО ПРЕДЕЛЬНЫМ УСИЛИЯМ
Прямоугольные сечения с симметричной арматурой
3.56. Проверку прочности прямоугольных сечений с симметричной арматурой (когда 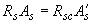 ) производят из условия
) производят из условия
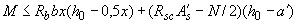 , (3.91)
, (3.91)
где 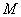 - момент относительно центра тяжести сечения, определяемый с учетом прогиба элементов согласно пп.3.53-3.55;
- момент относительно центра тяжести сечения, определяемый с учетом прогиба элементов согласно пп.3.53-3.55;
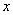 - высота сжатой зоны, принимаемая равной
- высота сжатой зоны, принимаемая равной
а) при 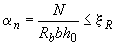 (черт.3.27) -
(черт.3.27) - 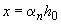 ;
;
б) при 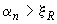 -
- 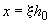 ,
,
где 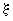 определяется по формуле
определяется по формуле
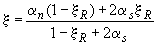 ; (3.92)
; (3.92)
здесь 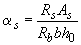 ;
;
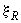 - см. табл.3.2.
- см. табл.3.2.
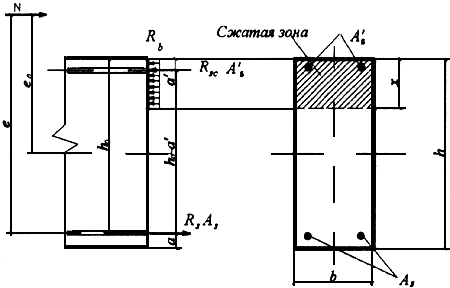
Черт.3.27. Схема усилий в поперечном прямоугольном сечении внецентренно сжатого элемента
3.57. Требуемое количество симметричной арматуры определяется следующим образом в зависимости от относительной величины продольной силы 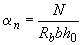 :
:
а) при 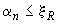
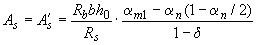 , (3.93)
, (3.93)
б) при 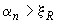
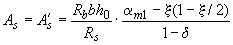 , (3.94)
, (3.94)
где 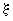 - относительная высота сжатой зоны, определяемая по формуле (3.92), где значение
- относительная высота сжатой зоны, определяемая по формуле (3.92), где значение 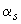 допускается принимать равным
допускается принимать равным
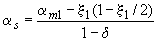 (3.95)
(3.95)
при 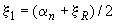 , но не более 1,0.
, но не более 1,0.
В формулах (3.93-3.95):
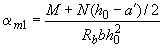 ,
, 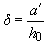 ;
;
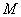 - см. пп.3.53-3.55.
- см. пп.3.53-3.55.
Если значение 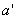 не превышает 0,15
не превышает 0,15 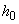 , необходимое количество арматуры можно определять с помощью графика черт.3.28, используя формулу
, необходимое количество арматуры можно определять с помощью графика черт.3.28, используя формулу
Дата добавления: 2017-02-20; просмотров: 911;
