Линейные пространства

Линейным пространством L над полем F называют множество элементов 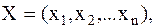называемых векторами, для которых заданы две операции:

­ сложение векторов;

­ умножение векторов на элементы из поля F.

Поле 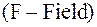(F – Field) – это конечное множество, состоящее из «m» элементов, в котором определены правила для выполнения математических операций. Основное отличие их от обычных математических операций в том, что они выполняются над конечным числом элементов.

Нормированные пространства

Следующий шаг в совершенствовании структуры пространства сигналов – объединение геометрических и алгебраических операций путём введения действительного числа, характеризующего «размер» элемента в пространстве. Такое число называется нормой вектора и обозначается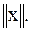

В качестве нормы можно использовать любое отображение линейного пространства на действительную ось, удовлетворяющее аксиомам:

1.

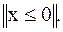
2.

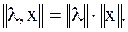
3.

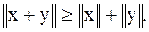
Множество векторов называют линейно независимыми, если равенство 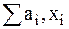возможно только лишь при всех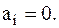

Понятие базиса

Система линейно независимых и ненулевых векторов 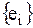образует в пространстве L базис, если для всех х, принадлежащих L, существует 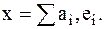Благодаря введению базиса операции над векторами превращаются в операции над числами (координатами).

Представление сигналов векторами и введение в рассмотрение пространств сигналов значительно упрощает анализ и синтез систем связи, позволяет эффективно решать проблемы повышения помехоустойчивости и пропускной способности.

Выводы

1. Введение понятия пространства, нормы, метрики, базиса позволяет формализовать процессы, связанные с передачей и приемом сигналов.