Метрические пространства

Первым свойством, которым наделим пространство сигналов, называют метрикой.

Метрическое пространство – это пространство с подходящим образом определённым расстоянием между его элементами. Само это расстояние, как и способ его определения называют метрикойи обозначают: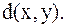

С понятием расстояния человек сталкивается повседневно, связывая это понятие с пространственным размещением предметов и понимая под расстоянием меру удалённости предметов, друг от друга. Обычно расстояние между двумя точками измеряется длиной отрезка, соединяющего эти точки. Однако такое определение расстояния часто оказывается недостаточным. Так, в обиходе расстояние между двумя городами определяется не однозначно (расстояние по железной дороге, расстояние по водному пути и т.п.). В городе, разделённом на кварталы, измерять расстояние отрезками прямой, соединяющей две точки, не имеет смысла, так как двигаться можно только по улицам. С другой стороны, слово удалённость часто не связывают с пространством в обычном понимании. Так, близость двух клеточек на шахматной доске можно оценить числом ходов, которые нужно сделать, чтобы перевести шахматную фигуру с одной клеточки на другую. При этом две соседние клеточки близки для короля, но далеки для коня и являются бесконечно далёкими, если из одной в другую нужно перевести слона. Из приведенных примеров видно, что должно существовать некоторое общее определение расстояния как меры удалённости объектов.

Понятия отображения и функционала: Пусть X и Y некоторые множества и множество M является подмножеством X·Y, причём ПР₁ M=X

Метрика должна представлять собой функционал: отображение любой пары элементов x и y множества на действительную ось должно удовлетворять аксиомам:

1. 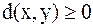(равенство 0 при 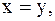аксиома идентичности).

2. 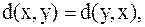– аксиома симметрии.

3. 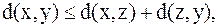– аксиома треугольника.

Следует иметь ввиду, что метрики можно задать разными способами и в результате для одних и тех же элементов получить разные пространства.

Следовательно, метрика определяет геометрические свойства сигналов.

Усовершенствуем структуру пространства сигналов, наделив его простым алгебраическим свойством, присущим реальным сигналам, которые можно алгебраически складывать и умножать на числа.