Метрические и линейные пространства

Понятие множества является фундаментальным неопределяемым понятием. Под множествомбудем понимать совокупность определённых вполне различаемых объектов, рассматриваемых как единое целое. Можно говорить о множестве стульев в комнате, студентов в учебной группе, букв в алфавите и т. д. При этом о множестве можно вести речь только тогда, когда элементы множества различимы между собой. Например, нельзя говорить о множестве капель в стакане воды, так как невозможно чётко и ясно выделить каждую отдельную каплю.

Отдельные объекты, из которых состоит множество, называют элементами множества. Так, число 3 – элемент множества натуральных чисел, а буква б – элемент множества русского алфавита.

Общим обозначением множества служит пара фигурных скобок, внутри которых перечисляются элементы множества. Для обозначения конкретных множеств используют различные прописные буквы А,S,X…или прописные буквы с индексами 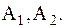Для обозначения элементов множества в общем виде используют различные строчные буквы a,s,x…или строчные буквы с индексами a₁,a₂…

Для указания того, что некоторый элемент a является элементом множества S используется запись:a 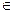S. Множества бывают конечными и бесконечными. Множество называют конечным, если число его элементов конечно. Множество называют бесконечным, если оно содержит бесконечное число элементов.

Говорят, что множество имеет структуру, если между элементами множества установлены определённые соотношения или над ними определены некоторые операции. Множество, наделённое структурой, называют пространством.

Можно дать другое определение пространства: множество объектов (любой физической природы), наделённых некоторым общим свойством. Свойства, которыми целесообразно наделять пространства сигналов, должны отражать наиболее существенные свойства реальных сигналов: 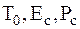и т. д.