Пространства со скалярным произведением
Введём еще одну дополнительную характеристику в пространстве сигналов в отображения упорядоченной пары векторов на поле скаляров из F.
Эту операцию называют скалярным (внутренним) произведением векторов и записывают в виде: 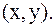
1. Если 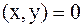 , то вектора х и у ортогональны.
, то вектора х и у ортогональны.
2. Если 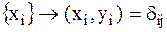 –символ Кронекера:
–символ Кронекера: 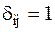 при
при 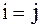 и
и
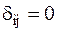 при
при 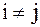 , система векторов – ортонормированная.
, система векторов – ортонормированная.
Система ортонормированных векторов линейно независимая.
В линейном пространстве со скалярным произведением норму и метрику целесообразно определять через скалярное произведение.
В ТЭС наибольший интерес представляют следующие линейные нормированные пространства:
1. 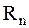 – n-мерное вещественное евклидово пространство, в котором каждый вектор определяется совокупностью n его координат.
– n-мерное вещественное евклидово пространство, в котором каждый вектор определяется совокупностью n его координат.
Скалярное произведение векторов в этом пространстве:
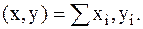
| (2.1) |
Оно порождает норму и расстояние:
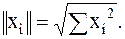
| (2.2) |
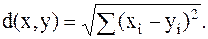
| (2.3) |
Пример:определения нормы и метрики Евклида в декартовой системе координат: заданы два вектора (сигнала) 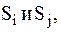 положение которых полностью определено их координатами
положение которых полностью определено их координатами 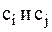 (рисунок 2.1).
(рисунок 2.1).
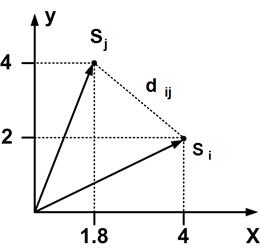
|
| Рисунок 2.1 – Определения нормы и метрики Евклида в декартовой системе координат |
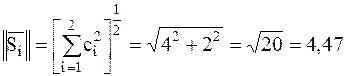
|
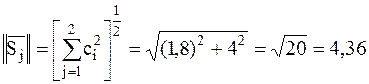
|
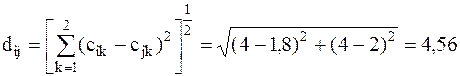
|
Расстояние между векторами 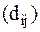 определяет различимость сигналов. Чем больше расстояние (метрика), тем лучше различимы сигналы. Метрика Евклида применяется при декодировании свёрточных кодов с помощью алгоритма Витерби с мягким решением. Выигрыш от применения мягкого решения в отношении сигнал/шум по сравнению с жёстким решением составляет 2,5 дБ (при квантовании продетектированного сигнала на 8 уровней).
определяет различимость сигналов. Чем больше расстояние (метрика), тем лучше различимы сигналы. Метрика Евклида применяется при декодировании свёрточных кодов с помощью алгоритма Витерби с мягким решением. Выигрыш от применения мягкого решения в отношении сигнал/шум по сравнению с жёстким решением составляет 2,5 дБ (при квантовании продетектированного сигнала на 8 уровней).
2. 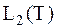 – бесконечномерное пространство Гильберта, которое образуют непрерывные комплексные или вещественные функции, заданные на интервале (0,Т):
– бесконечномерное пространство Гильберта, которое образуют непрерывные комплексные или вещественные функции, заданные на интервале (0,Т):
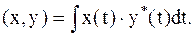
| (2.4) |
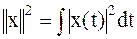 – квадрат нормы – это энергия сигнала, если под
– квадрат нормы – это энергия сигнала, если под 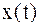 иметь ввиду напряжение (ток) на сопротивлении 1 Ом. Энергию разностного сигнала можно представить следующим выражением:
иметь ввиду напряжение (ток) на сопротивлении 1 Ом. Энергию разностного сигнала можно представить следующим выражением:
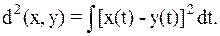
| (2.5) |
В пространстве Гильберта определяется квадрат расстояния между любой парой сигналов (векторов). Величина 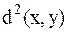 полностью характеризует различие между сигналами.
полностью характеризует различие между сигналами.
3. 2n – n-мерное пространство Хэмминга, которое образуют двоичные n-последовательности, широко используемые в системах связи.
Норма, метрика в этом пространстве:
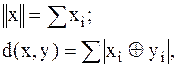
| (2.6) | |||
| где | 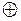
| – | суммирование по модулю «2». | |
Норма вектора в пространстве Хэмминга определяется общим количеством содержащихся в нём единиц, а расстояние между векторами – количеством позиций (разрядов) кодовых комбинаций, в которых они различаются.
Примеры:
1. Задана кодовая комбинация (вектор в пространстве Хэмминга): 1011010. Определить норму.
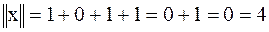 – норма данного вектора. Норма вектора в пространстве Хэмминга совпадает с количеством единиц в кодовой комбинации, т.е. с весом кодовой комбинации.
– норма данного вектора. Норма вектора в пространстве Хэмминга совпадает с количеством единиц в кодовой комбинации, т.е. с весом кодовой комбинации.
2. Заданы две кодовые комбинации: 1001011 и 0110010. Определить расстояние (метрику) в пространстве Хэмминга между кодовыми комбинациями.
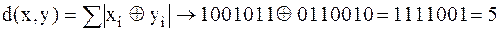
|
Метрика (расстояние) между кодовыми комбинациями равна 5. Метрика Хэмминга находит широкое применение при декодировании свёрточных кодов по алгоритму Витерби с жёстким решением. Чем больше метрика Хэмминга, тем сильнее различима кодовые комбинации.
Выводы
1. Векторное представление применимо как для детерминированных функций, так и для случайных. В последнем случае скалярное произведение, норма и расстояние – случайные величины.
3. Разложение сигналов в обобщённый ряд Фурье
Разложению в ряд Фурье могут подвергаться периодические сигналы. При этом они представляются в виде суммы гармонических функций, либо комплексных экспонент с частотами, образующими арифметическую прогрессию. Для того, чтобы такое разложение существовало, фрагмент сигнала длительностью в один период должен удовлетворять условиям Дирихле:
1. Не должно быть разрывов второго рода (с уходящими в бесконечность ветвями функции).
2. Число разрывов первого рода (скачков) должно быть конечным.
3. Число экстремумов должно быть конечным.
Ряд Фурье может быть применён для представления не только периодических сигналов, но и сигналов конечной длительности. При этом оговаривается временной интервал, для которого строится ряд Фурье, а в остальные моменты времени сигнал считается равным нулю. Для расчёта коэффициентов ряда такой подход фактически означает периодическое продолжение сигнала за границами рассматриваемого интервала.
Методы Фурье используются для анализа линейных схем или систем: для предсказания реакции (отклика) системы; для определения передаточной функции; для оценки результатов тестов.
Произвольный периодический сигнал 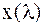 выражается через бесконечное число гармоник с возрастающими частотами:
выражается через бесконечное число гармоник с возрастающими частотами:
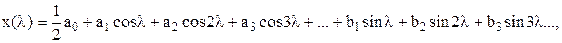
| (2.7) | |||
| где | 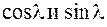
| – | основные члены; | |
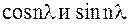
| – | гармонические члены (при n > 1, n – целое число); | ||
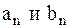
| – | коэффициенты гармоник; | ||
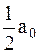
| – | постоянный член или составляющая постоянного тока. | ||
Период функции 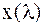 должен равняться 2π или кратной величине; кроме того функция
должен равняться 2π или кратной величине; кроме того функция 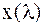 должна быть однозначной. Ряд Фурье можно рассматривать как «рецепт приготовления» любого периодического сигнала из синусоидальных составляющих. Чтобы данный ряд имел практическое значение, он должен сходиться, т.е. частичные суммы ряда должны иметь предел.
должна быть однозначной. Ряд Фурье можно рассматривать как «рецепт приготовления» любого периодического сигнала из синусоидальных составляющих. Чтобы данный ряд имел практическое значение, он должен сходиться, т.е. частичные суммы ряда должны иметь предел.
Процесс создания произвольного периодического сигнала из коэффициентов, описывающих смешивание гармоник, называется синтезом. Обратный процесс вычисления коэффициентов именуется анализом. Вычисление коэффициентов облегчается тем, что среднее от перекрёстных произведений синусоиды на косинусоиду (и наоборот) равно 0.
Введём в пространство Гильберта базис: 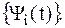 Для упрощения будем полагать, что он ортонормированный.
Для упрощения будем полагать, что он ортонормированный.
Тогда любую функцию 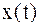 из пространства Гильберта можно представить через проекции
из пространства Гильберта можно представить через проекции 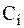 вектора х на оси базиса обобщённым рядом Фурье:
вектора х на оси базиса обобщённым рядом Фурье:
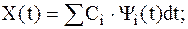
| (2.8) | |||
| где | 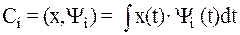
| – | коэффициент разложения в обобщённый ряд Фурье. | |
Ряды Фурье особенно полезны при описании произвольных периодических сигналов с конечной энергией каждого периода. Кроме того, они могут использоваться для описания непериодических сигналов, имеющих конечную энергию за конечный интервал. На практике для описания таких сигналов используют интеграл Фурье.
Выводы
1. Для описания периодических сигналов широко применяется ряд Фурье. Для описания непериодических сигналов используют интеграл Фурье.
Заключение
1. Сообщения, сигналы и помехи как векторы (точки) в линейном пространстве можно описать через набор координат в заданном базисе.
2. Для ТЭС наибольший интерес при отображении сигналов представляет n-мерное пространство Евклида 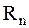 , бесконечное пространство Гильберта
, бесконечное пространство Гильберта 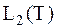 и дискретное пространство Хэмминга 2n. В этих пространствах вводится понятие скалярного произведения двух векторов (x,y).
и дискретное пространство Хэмминга 2n. В этих пространствах вводится понятие скалярного произведения двух векторов (x,y).
3. Любую непрерывную функцию времени как элемент 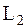 можно представить обобщенным рядом Фурье по заданному ортонормированному базису.
можно представить обобщенным рядом Фурье по заданному ортонормированному базису.
Литература
Основная:
1. Теория электрической связи: Учеб. Для вузов / А.Г. Зюко, Д. Д. Кловский, В.И. Коржик, М. В. Назаров; Под ред. Д. Д. Кловского. – М.: Радио и связь, 1998. – 433 с.
Дополнительная:
1. Прокис Дж. Цифровая связь: Пер. с англ. / Под ред. Д.Д. Кловского. – М.: Радио и связь, 2000. – 800 с.
2. Бернард Скляр. Цифровая связь. Теоретические основы и практическое применение: Пер. с англ. – М.: Издательский дом «Вильямс», 2003. – 1104 с.
3. Сухоруков А.С. Теория электрической связи: Конспект лекций. Часть 1. – М.:МТУСИ, ЦЕНТР ДО, 2002. – 65 с.
4. Сухоруков А.С. Теория цифровой связи: Учебное пособие. Часть 2. – М.:МТУСИ, 2008. – 53 с.
Дата добавления: 2017-10-09; просмотров: 1253;
