Дифференциальное уравнение

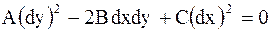
(2.58)

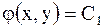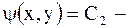называется характеристическим уравнением для уравнения (2.52), а его общие интегралы и характеристиками.

Характеристики линейного уравнения (2.52) используются для приведения его к каноническому виду. Уравнение (2.52) в каждой из областей, где сохраняется знак дискриминанта 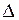, приводится к эквивалентному уравнению, а именно к каноническому, путем введения вместо переменных 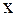и 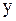новых переменных 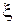и 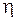с помощью зависимостей

.

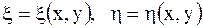Для уравнения гиперболического типа характеристическое уравнение имеет два интеграла, т.е. существуют два семейства действительных характеристик

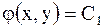и ,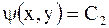

и потому следует сделать замену переменных, положив

,

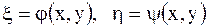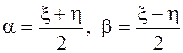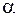в результате чего исходное уравнение преобразуется к уравнению (2.54) (или к уравнению (2.55) после дополнительной замены , где и 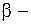новые переменные).

Для уравнения параболического типа характеристическое уравнение имеет один действительный интеграл, т.е. одну характеристику 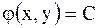, и потому полагают

,

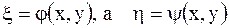где 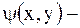произвольная функция, например, 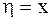. После такой замены уравнение приводится к виду (2.56).

Для уравнения эллиптического типа общие интегралы характеристического уравнения имеют вид

,

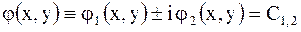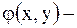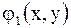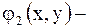где функция, принимающая комплексные значения, а и действительные функции действительных переменных. С помощью подстановок

уравнение (2.52) приводится к каноническому виду (2.57).

После выбора новых переменных 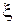и 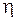требуется преобразовать производные, входящие в данное уравнение, к новым переменным. Напомним, что первые производные по старым переменным 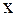и 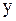выражаются через производные по новым переменным 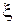и 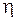по известным формулам дифференцирования сложной функции двух переменных:

.

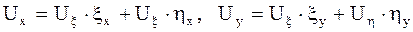Вторые производные находятся путем дифференцирования выражений для 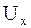и 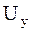по правилу дифференцирования сложной функции.

Так как для каждого типа канонических уравнений разработаны определенные методы как аналитического, так и численного решения, то задача приведения уравнений (2.52) к каноническому виду представляет практический интерес.

Заметим, что в различных областях тип одного и того же уравнения (2.52) может быть различным.