Объект моделирования – ПТМ

ПТМ – система, состоящая из множества элементов. Это множество можно разбить на четыре группы. К ним относятся элементы металлоконструкции, приводы или механизмы, электрооборудование и прочее и вспомогательное оборудование (Рис. 8). В вою очередь, полученные группы содержат подгруппы, состоящие из подгрупп более низкого уровня, и т.д. Степень детализации зависит от целей разработчика.

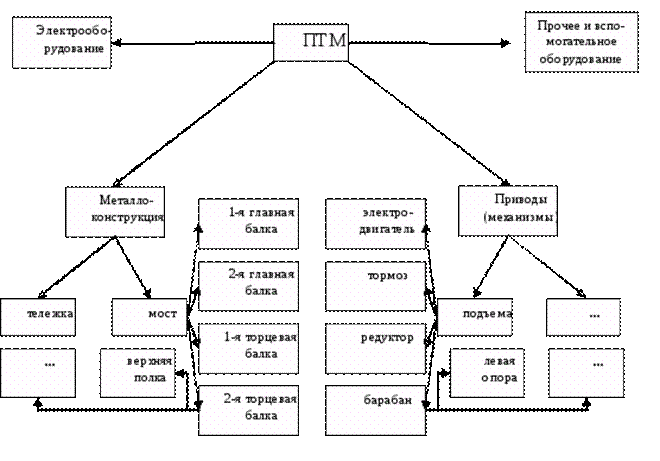
Рис. 8 Структурная схема ПТМ (мостового крана)

Элементы металлоконструкции ПТМ – это балки, фермы, колонны. Они обладают объемом и массой, которая распределяется по объему элемента по некоторому закону (Рис. 9).

а) стрела портального крана б) мост мостового крана

Рис. 9 Металлоконструкции ПТМ.

Однако чаще всего они рассматриваются как стержневые системы, масса которых может быть как распределена по длине, так и сосредоточена в нескольких точках или точке, как правило, центре масс элемента. При этом инерционными характеристиками элементов модели являются приведенная масса или приведенный момент инерции. Приведение последних производится на основании равенства кинетических энергий реального элемента и элемента с приведенной массой и осуществляется по следующим зависимостям

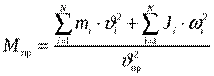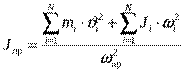или ,(13)

где m_i и J_i – инерционные характеристики элементов конструкци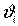и, и 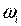– скорости движения элементов конструкции в поступательном и вращательном движении, соответственно, 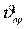и 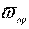- скорости движения элемента с приведенной массой в поступательном и вращательном движении, соответственно.

Также элементы металлоконструкции обладают упругостью, т.е. способностью восстанавливать форму после снятия нагрузки, вызвавшей изменение формы элемента. Реальные элементы металлоконструкции обладают линейной упругостью по осям X, Y, Z и изгибной или крутильной упругостью в плоскостях XOY, XOZ, YOZ. Упругость элементов металлоконструкции характеризуется коэффициентом жесткости, угловым или линейным, в зависимости от вида деформации. Как правило, при моделировании учитывается тот тип упругости элемента, который соответствует наибольшей его деформации. При замене оригинала элементом модели последний характеризуется коэффициентом жесткости, определенным на основании равенства потенциальных энергий реального и моделируемого объектов по зависимостям

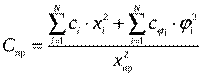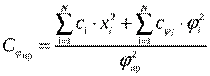или ,(14)

где c_i и 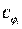– жесткостные характеристики элементов конструкции, x_i и 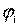– деформации элементов конструкции в поступательном и вращательном движении, соответственно, x_пр и 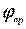- деформации элемента с приведенным коэффициентом жесткости в поступательном и вращательном движении, соответственно.

При работе ПТМ элементы ее металлоконструкции совершают сложное пространственное движение. Учет упругости элементов кроме переносного и относительного движения элементов конструкции, соответствующих выполнению основных рабочих движений, предполагает рассмотрение упругих колебаний, возникающих в элементах конструкции из-за взаимодействия сил упругости и сил инерции.

Рассмотрим, к примеру, портальный кран (Рис. 10).

Рис. 10 Портальные перегрузочные краны.

Работая, кран совершает следующие движения: поворот, подъем/опускание груза и изменение вылета. Также возможно перемещение крана вдоль штабеля груза по крановым путям. Для увеличения рабочей площади, которую может обработать кран, применяются т.н. стрелы с рабочим изменением вылета. Качание стрелы происходит в интервале от минимального до максимального вылета. При этом обрабатываемая краном площадь увеличивается, но центры тяжести стреловой системы и груза поднимаются на некоторую величину, что требует дополнительных затрат энергии. Уменьшение или исключение этих затрат достигается при помощи уравновешивания веса груза и собственного веса стрелового устройства. Для уравновешивания веса груза используются специальные устройства, называющиеся уравновешенными стрелами. Уравновешивание веса груза состоит в обеспечении близкой к горизонтали траектории перемещения груза при изменении вылета стрелы. Для чего используются четырехзвенные стреловые системы, называемые шарнирно-сочлененные устройства (ШСУ). ШСУ бывают с прямым и профилированным хоботами, с гибкой и жесткой оттяжками. ШСУ с прямым хоботом и жесткой оттяжкой (Рис. 10) представляет собой шарнирный четырехзвенник Чебышева, предназначенный для преобразования вращательного движения входного звена в поступательное выходного. На большей части своей траектории конец выходного звена четырехзвенника перемещается по пологой кривой линии, близкой к горизонтали. Выполнение краном рабочих движений приводит к появлению раскачивания груза на канатах в плоскости вылета и из плоскости вылета стрелы. Если ограничиться плоскостью вылета и не учитывать упругость элементов стреловой системы, ее можно представить следующей расчетной схемой (Рис. 11), где реальные элементы металлоконструкции заменены двухопорными балками с сосредоточенными в центрах тяжести элементов массами.

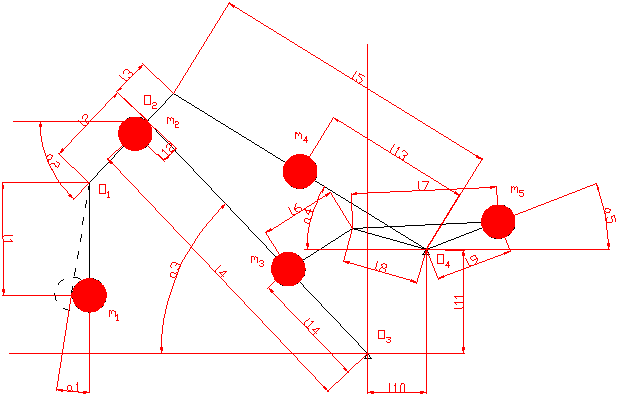
Рис. 11 Расчетная схема стреловой системы.

На схеме представлены основные элементы стреловой системы: хобот, стрела, оттяжка, противовес, соединенный со стрелой тягой, и груз, подвешенный на канатах. На схеме обозначены: l1 - длина канатной подвески, размеры l2 и l3 - хобота, l4 - стрелы, l5 - оттяжки, l6 - тяги противовеса, l7, l8 и l9 -противовеса, l10 и l11 - положение точки крепления оттяжки, m1, m1, m1, m1 и m1 - массы груза, хобота, стрелы, оттяжки и противовеса, соответственно, l12, l13 и l14 - положения центров масс хобота, оттяжки и стрелы, соответственно. При изменении вылета происходит вращение перечисленных элементов около шарниров, обозначенных буквами O с индексами. Поскольку модель жесткая, т.е. все элементы абсолютно жесткие, то положения всех элементов, а, значит, и их скорости являются функциями вылета (скорости изменения вылета) или угла наклона стрелы (скорости изменения угла наклона стрелы).

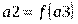
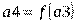
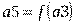
Таким образом, при составлении расчетной схемы для жесткой модели стреловой системы нет необходимости рассматривать все элементы ШСУ по отдельности и можно ограничиться двухмассовой расчетной схемой с двумя обобщенными координатами (Рис. 12).

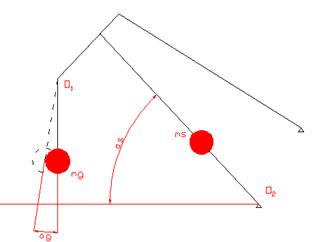
Рис. 12 Расчетная схема стреловой системы

На схеме обозначены следующие обобщенные координаты модели: ag - угол отклонения грузовых канатов от вертикали, as - угол наклона стрелы к горизонтали; приведенные массы: mg - масса груза и грузозахватного устройства, ms - приведенная к точке крепления тяги масса элементов стрелового устройства.

Массу m2 найдем по зависимости (13). Движение масс системы, изображенной на схеме (Рис. 11), является сложным. Для записи выражения для кинетической энергии целесообразно воспользоваться следующим алгоритмом. Сначала определим декартовы координаты масс системы, приняв за начало координат в каждом случае наиболее удобную точку. Затем, дифференцируя по времени полученные координаты, найдем проекции скоростей масс на оси координат и, далее, квадраты абсолютных скоростей масс.

1) Для массы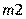

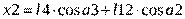
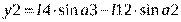
Для массы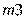

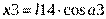
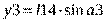
Для массы

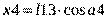
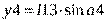
Для массы

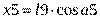
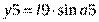
2)

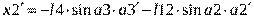
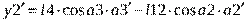
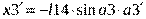
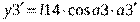
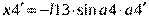
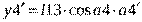
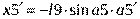
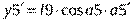
3)

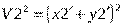
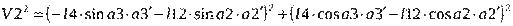
или упрощая

.

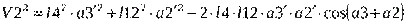Второе слагаемое выражения характеризует кинетическую энергию массы 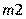при качании относительно точки 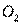, оставшиеся относительно точки 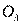и т.д.

Тогда выражение для кинетической энергии масс системы можно записать в виде

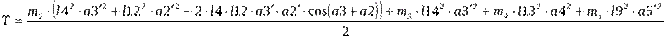
а для приведенной массы

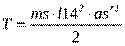, где 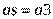. Отсюда найдем приведенную массу.

В тех случаях, когда при моделировании необходимо учесть колебательные процессы, протекающие в элементах металлоконструкции, количество степеней свободы и обобщенных координат, а также дискретных масс существенно увеличивается.

Рис. 13 Виды стержней.

В случаях сложного движения () необходимо учитывать

Воздействия приводов складываются из воздействий двигателей и тормозов механизмов.

При моделировании допускается воздействия тормозов механизмов рассматривать в виде прямоугольных импульсов, т.е. считаем, что момент тормоза прикладывается мгновенно и по величине равен нормативному значению.

Воздействия механизмов задаются с помощью механических характеристик двигателей с учетом передаточного отношения механизма.

Основной характеристикой двигателя является механическая характеристика, функциональная зависимость, выражающая связь между скоростью двигателя и моментом, который он создает.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Моделирование. Определения, виды моделирования.

2. Модель. Определения, виды моделей.

3. Математические модели. Определения, виды математических моделей.

4. Системы, свойства систем, структура системы.

5. Человеко-машинные системы (ЧМС), подъемно-транспортные машины (ПТМ), подъемно-транспортные системы (ПТС).

6. Принципы математического моделирования.

7. Свойства математических моделей.

8. Последовательность этапов математического моделирования.

9. Концептуальная модель (расчетная схема).

10. Среда, как объект моделирования. Виды воздействий среды на ПТМ и человека-оператора (ЧО).

11. Человек-оператор, как объект моделирования. Виды воздействий ЧО на ПТМ и окружающую среду.

12. Способы учета ЧО при выдаче управляющих воздействий.

13. ПТМ, как объект моделирования.

14. Цели моделирования.

15. Этапы составления концептуальной модели.

16. Способы моделирования процесса осуществления управляющих воздействий.

17. Оптимальная стратегия управления. Способы выбора оптимальной стратегии.

18. Случайное событие, случайная величина, характеристики случайной величины.

19. Моделирование силовых воздействий окружающей среды на элементы ПТМ.

20. Моделирование воздействий приводов ПТМ.

21. Структура системы ПТМ.

22. Свойства элементов металлоконструкции ПТМ, учитывающиеся при моделировании.

23. Свойства элементов приводов ПТМ, учитывающиеся при моделировании.

24. Структура привода ПТМ.

25. Особенности различных типов приводов ПТМ.

26. Декомпозиция системы при составлении концептуальной модели.

27. Способы представления элементов металлоконструкции ПТМ при составлении расчетной схемы.

28. Пример составления расчетной схемы для жесткой модели мостовой тележки.

29. Пример составления расчетной схемы для упругой модели мостовой тележки.

30. Способы задания модельного времени.

31. Способы составления моделей и типы моделей в зависимости от вида информации о моделируемом объекте.

32. Регрессионные модели.

33. Планируемый факторный эксперимент (ПФЭ).

34. Факторы, виды факторов, интервалы варьирования факторов.

35. Границы применимости модели.

36. Методы оценки степени влияния количественных факторов на отклик.

37. Методы оценки степени влияния качественных факторов на отклик.

38. Свойства матрицы планирования и определение коэффициентов регрессии.

39. Метод наименьших квадратов.

40. Проверка адекватности модели.

ЛИТЕРАТУРА

1. Александров М.П. Подъемно-транспортные машины. - М.: Высшая школа, 1985. 520 с.

2. Артоболевский И. И. Теория машин и механизмов. - М.: Наука, 1988. 638 с.

3. Бать М. И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в примерах и задачах. В 2-х т. Т. 1. М.: Наука, 1966. 632 с.

4. Бать М. И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в примерах и задачах. В 2-х т. Т. 2. М.: Наука, 1966. 664 с.

5. Бидерман В. Л. Теория механических колебаний. - М.: Высшая школа, 1980. 480 с.

6. Брауде В.И., Тер-Мхитаров М.С. Системные методы расчета грузоподъемных машин. - Л.: Машиностроение, 1985. 181 с.

7. Вайнсон А.А. Подъемно - транспортные машины. - М.: Машиностроение, 1989. 431 с.

8. Вентцель Е.С. Теория вероятностей. - М.: Наука, 1962. 576 с.

9. Вибрации в технике: Справочник: В 6-ти т. Т. 6 / Под ред. К. В. Фролова. – М.: Машиностроение, 1995. 456 с.

10. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высш. школа, 1977. 479 с.

11. Гнеденко Б.В. Курс теории вероятностей. - М.: Наука, 1988. 448 с.

12. Головачев П.А., Гладунко Ю.И. Техническая эксплуатация и монтаж подъемно - транспортных машин. - М.: Транспорт, 1985. 304 с.

13. ГОСТ 26387-84 Система "человек-машина". Термины и определения.

14. Гохберг М.М. Металлические конструкции подъемно - транспортных машин. - Л.: Машиностроение, 1976. 450 с.

15. Григорьев Н.И. Нагрузки кранов. - М. - Л.: Машиностроение, 1964. 168 с.

16. Грузоподъемные машины / М.П. Александров, Л.Н. Колобов, Н.А. Лобов и др. - М.: Машиностроение, 1986. 395 с.

17. Гультяев А. К. MATLAB 5.2. Имитационное моделирование в среде Windows: Практическое пособие. – СПб.: КОРОНА принт, 1999. – 288 с.

18. Дьяконов В.П. Справочник по алгоритмам и программам на языке Бейсик для персональных ЭВМ. - М.: Наука, 1989. 240 с.

19. Игнатьев Н. Б., Ильевский Б. З., Клауз Л. П. Моделирование системы машин. – Л.: Машиностроение, 1986. 423 с.

20. Информационно-управляющие человеко-машинные системы: Исследование, проектирование, испытание: Справочник / А. А. Адаменко, А. Т. Ашеров и др. - М.: Машиностроение, 1993. 494 с.

21. Комаров М. С. Динамика грузоподъемных машин. - М.: Машгиз, 1962. 267 с.

22. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. - М.: Наука, 1984. 832 с.

23. Лобов Н. А. Динамика грузоподъемных кранов. - М.: Машиностроение, 1987. 376 с.

24. Математический энциклопедический словарь. / Гл. ред. Ю. В. Прохоров. - М.: Советская энциклопедия, 1988. 847 с.

25. Мостеллер Ф., Тьюки Дж. Анализ данных и регрессия. - М.: Финансы и статистика, 1982. 319 с.

26. Налимов В. В. Теория эксперимента – М.: Наука, 1971. 207 с.

27. Научно-технический прогресс. / Словарь. – М.: Политиздат, 1987. 366 с.

28. Павлов Н. Г. Примеры расчетов кранов. - Л.: Машиностроение, 1976. 320 с.

29. Правила устройства и безопасной эксплуатации грузоподъемных кранов. - СПб.: Издательтво ДЕАН, 2004. - 272 с.

30. Рачков Е. В., Силиков Ю. В. Подъемно - транспортные машины и механизмы. - М.: Транспорт, 1989. 240 с.

31. Себер Дж. Линейный регрессионный анализ. - М.: Мир, 1980. 456 с.

32. Справочник по кранам / в 2 т. Т. 1; Под общ. ред. М. М. Гохберга. - Л.: Машиностроение, 1988. 536 с.

33. Справочник по кранам / в 2 т. Т. 2; Под общ. ред. М. М. Гохберга. - Л.: Машиностроение, 1988. 559 с.

34. Шерле З. П. Каракулин Г. Г. Справочник механизатора речного порта. – М.: Транспорт, 1980. 391 с.

35. Тер-Мхитаров М.С. Оператор перегрузочных машин. – Пермь: Кн. изд-во, 1982. – 140 с.

ОММ

Введение

Оглавление | Назад | Далее | Глоссарий понятий

Моделирование в научных исследованиях стало применяться еще в глубокой древности и постепенно захватывало все новые области научных знаний. Большие успехи и признание практически во всех отраслях современной науки принес методу моделирования ХХ в. Однако, методы моделирования долгое время развивалась независимо отдельными науками. Отсутствовала единая система понятий, единая терминология. Количественный аспект анализа экономических явлений и процессов всегда занимал большое место в работах классиков отечественной и зарубежной экономики. Например, еще в 1938 г. французский математик Курно в работе «Исследование математических принципов теории богатства» сформулировал «закон спроса». Ф. Кэнэ создал «экономическую таблицу», являющую собой попытку представить в форме математической модели процесс воспроизводства общественного продукта как единого целого.

Математическое моделирование – это теоретико-экспериментальный метод позновательно-созидательной деятельности, метод исследования и объяснения явлений, процессов и систем (объектов-оригиналов) на основе создания новых объектов – математических моделей.

Существующие математические методы и модели позволяют решать задачи даже и большей размерности и учитывать большое число показателей и факторов влияния, а время решения задач значительно сокращается с применением компьютера.

Математические моделирование - наука, занимающаяся разработкой и практическим применением методов наиболее оптимального управления организационными системами.

Предмет математического моделирования - системы организационного управления или организации, которые состоят из большого числа взаимодействующих между собой подразделений не всегда согласующихся между собой и могут быть противоположны.

Цель математического моделирования - количественное обоснование принимаемых решений по управлению организациями.

Решение, которое оказывается наиболее выгодным для всей организации называется оптимальным, а решение наиболее выгодное одному или нескольким подразделениям будет субоптимальным.